浅谈傅里叶——3. 傅立叶收敛性证明与非周期信号的推广

从《浅谈傅里叶1》给出了傅里叶公式的三角函数和形式，并且通过欧拉公式作为桥，将实数平面的三角函数和映射到了复平面上，于是在《浅谈傅里叶2》中，有了我们常见的以复指数形式表达的傅里叶公式形式，并且给出了正交性的结论与表达方法。
在本章中，我们将试图证明傅里叶函数的收敛与收敛条件。如果傅里叶级数无法收敛，那么对于给定周期函数f(t)，我们就无法对原信号进行拟合f(t)。

关于傅里叶级数的收敛性

证明傅里叶级数对于一般连续函数的收敛性，是比较复杂的。从工作经验来看，其实并不能百分百的还原或者拟合原函数，误差其实一直都存在。所以，在信号学的实际工作环境中，有被称为吉布斯现象（Gibbs phenomenon）¹的存在。

有论文指出，当选取的傅里叶级数的项数N增加时，合成的波形虽然更逼近原函数，但在不连续点附近会出现一个固定高度的过冲，N越大，过冲的最大值越靠近不连续点，但其峰值并不下降，而是大约等于原函数在不连续点处跳变值的9%，且在不连续点两侧呈现衰减振荡的形式

那么对于比较平滑的连续函数来说，傅里叶就有比较好的拟合程度。所以，这里我们就要提出一个数学性的问题，也就是对于特定函数的求解，解决它的方法是否可以收敛，说人话也就是指会聚于一点，向某一值靠近。因此对于复杂的原始信号的“拆解”，那么傅里叶级数的收敛性证明就是十分重要的了。

狄利克莱收敛定理

最常见的一个手段，就是直接扔一个定理，这玩意称为**“狄利克莱收敛定理”**，它要求原函数在周期$2\pi$，并满足一下条件，即收敛

• 在一个周期区间内连续或只有有限个第一类间断点²
• 在一个周期区间内只有有限个极值点

则$f(x)$的傅里叶级数收敛，且有如下性质：

$$\frac{a_0}{2}+\Sigma (a_n\cos nx+b_n\sin nx)=\{\begin{array}{cc}f(x)& x为连续点\\ \frac{f(x+0)+f(x-0)}{2}& x为间断点\end{array}$$

傅里叶级数不能收敛的情况

比方说，对于以第二类间断的函数，就没办法用傅里叶级数进行拟合³。所以说，无论是做题，还是处理信号，如果遇到了这种类似的问题，你可能需要考虑使用其他方法去解决，而不是万能的用傅里叶级数去近似逼近原始函数信号。

傅里叶分析与非周期信号

从热力学的角度看，这个世界不存在无限振荡的周期信号，即便是一个正弦信号，也会因为能量衰减，到最后某一时刻信号消失。所以说，正余弦信号，是理想的信号，因为它在正负轴无限延长，并且不存在能量衰减。

所以，严格来说，我们无法对非周期信号，或者有能量衰减的信号使用傅里叶分析。但是通过一些特殊的处理方法，我们可以让这些信号适用于傅里叶分析。

比方说，对于非周期的信号，可以通过“复制、平移”的方式，把这个非周期信号转换成为周期信号

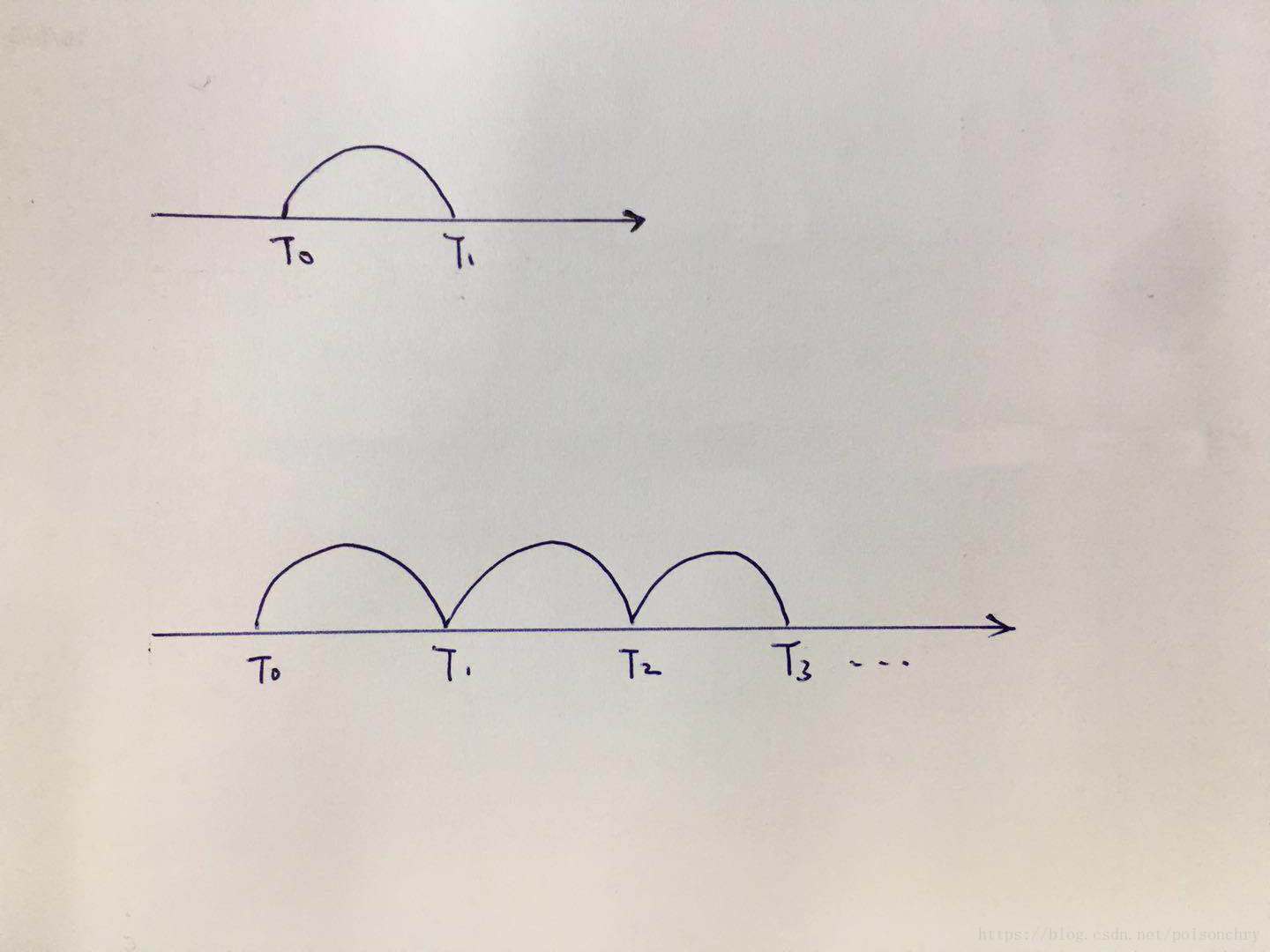
这就是我们分析非周期信号常用的技巧。

如何阅读傅里叶频谱图

傅里叶分析由于对于信号进行了完整的时域分析，于是可以得出信号包含的全部频率信息。例如对于50Hz的正弦信号，通过FFT(Fast Fourier Transform)可以获得一个频谱图如下：

由于FFT算法采用蝶形计算，所以对比DFT(Discret Fourier Transform)，它的图形是对称的（这也是因为傅里叶级数是关于实轴对称的共轭复数，所以为了快速计算，算法设计者只处理了一半的数据），实际上我们只需要关心其图形的一半。坐标轴X上的数值表示对应第50个维度的地方，就是50Hz频率所在位置，因此，X轴也被称为正弦信号的频率。

而纵轴Y轴，数的含义则没有意义，参考傅里叶公式，我们可以知道由复数形式表示的傅里叶级数，其系数是一个包含了振幅、相位等信息的常熟，某些地方Y轴也被成为正弦信号的加权常数。

所以对于频率图来说，我们只关心在具体频率分量位置，即对于
$$FFT(n)>0$$
是否出现了大于0的数。大于0时，表示该频率存在，频率大小为：

$$FFT(n)=n\times \frac{F_{sampling}}{Len(FFT)}$$

否则就是没有频率。

其中，$F_{sampling}$是指信号采样率，单位时间为1秒钟；$Len(FFT)$是复数数组长度，比如你用1024长的复数数组计算某个信号的频率，n是对应的bin的频率。

例如，采样率为1024Hz，FFT数组长度也是1024，那么对于：

$$FFT(0)=0Hz$$
$$FFT(1)=1\times \frac{1024}{1024}=1Hz$$
$$FFT(2)=2\times \frac{1024}{1024}=2Hz$$
$$...$$

这些知识点对于二维是一样的，所以很容易扩展到二维甚至高维情况。

---

1. 吉布斯现象 ↩︎

2. 第一类间断点 ↩︎

3. 第二类间断点 ↩︎