阿尔法α-贝塔β剪枝

1、简单的说明：一开始α和β是负正无穷，α表示到目前为止路径上发现的MAX的最佳(即极大值)选择，β表示到目前为止路径上发现的MIN的最佳(即极小值)选择。

α-β搜索中不断更新α和β的值，并且当某个节点的值分别比目前的MAX的α或者MIN的β的值更差时剪裁此节点剩下的分支(即终止递归调用)。

2、开始：每一个节点上都标明了可能的取值范围，先从B下面第一个叶节点3开始，这时作为MIN节点的B值最多为3。如下图所示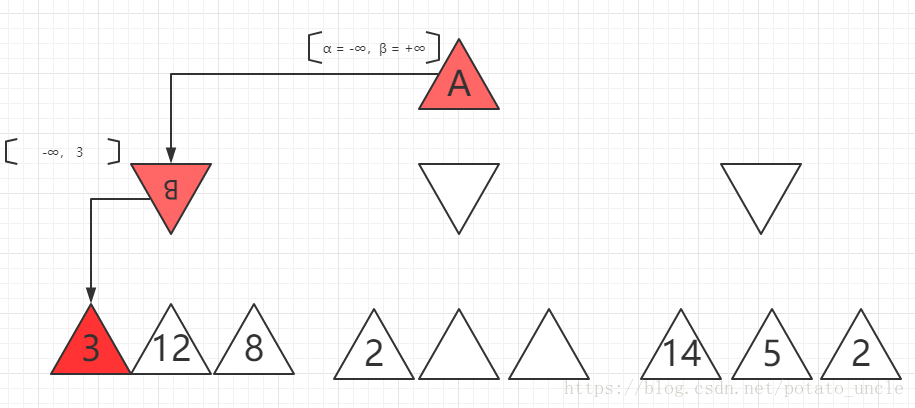

3、B下的第二个值为12，比3大，由于B想要最小值，则不考虑12，但却是会拿12与3作比较，所以12也会被算法计算到，此时MIN还是为3，8同理。此时已观察了B的所有后继，确定了最终的B的值为3，如下图所示。

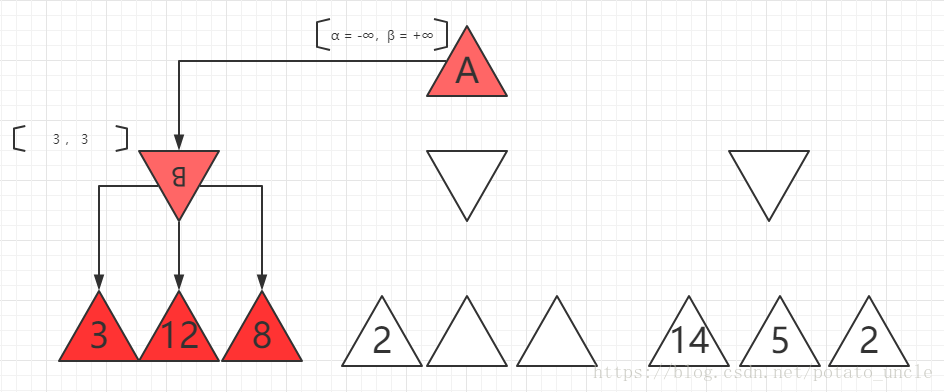
4、当C下面第一个后继为2，则C的MIN最多为2，此时B的值为3大于C的2，由于A要选MAX值，最少就是3不会再考虑C了，即C的另外两个后继不论是取何值，均不会再考虑了，此时我们就把C的另外两个后继裁剪掉，这就是α-β剪枝的实例。如下图所示。

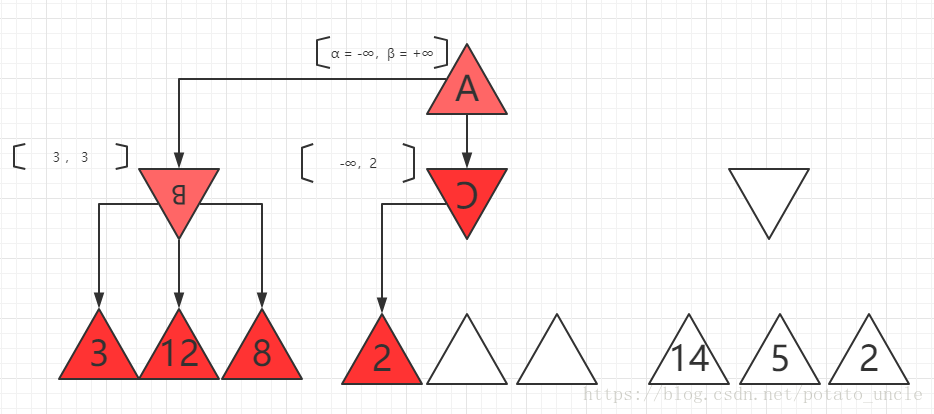
5、D下面第一个值为14，则D的值最多为14（比B的3要大，则继续向后探索），如下图所示。

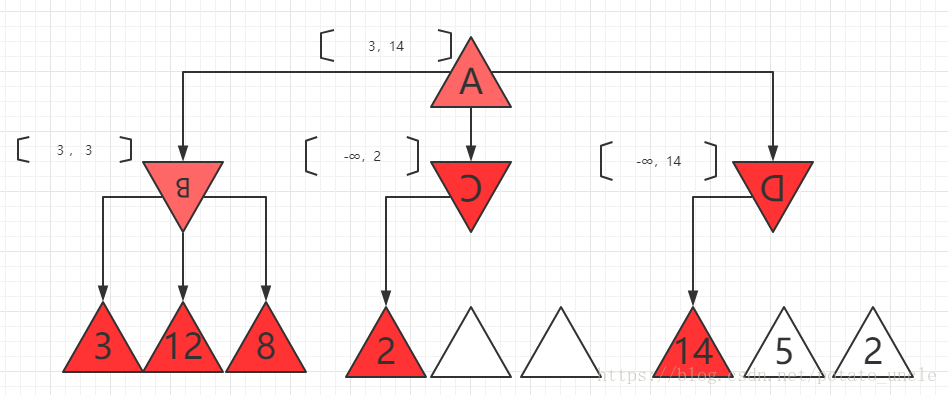
6、D继续向后探索，第二个值为5比14小，则D最大为5（此时仍比B的3大，继续向后探索），D的最后一个后继是2，则D最后的值为2，小于B的3，则最终MAX在根节点的决策是走向值为3的B节点。如下图所示。

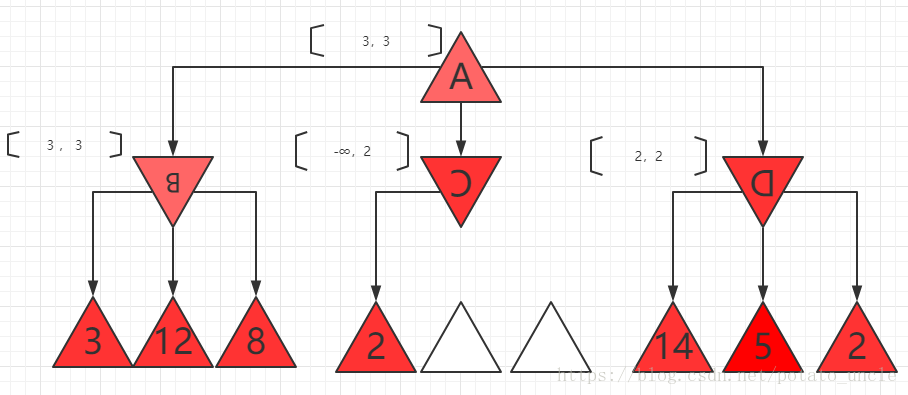
7、还可以把这个过程看作对MINIMAX公式的简化。根节点的值计算如下：

MINIMAX(root) = max( min(3, 12, 8), min(2, x, y), min( 14, 5, 2) )

                         = max( 3, min(2, x, y), 2)

                         = max(3, z, 2)      其中z = min(2, x, y) <= 2

                         = 3

其实可以理解为B,C,D需要各自后继的最小值，A需要B,C,D的最大值。

转载请与本人说明情况。

如果你也觉得很不错，那就请一键三连吧~