欧拉公式，为何如此优美

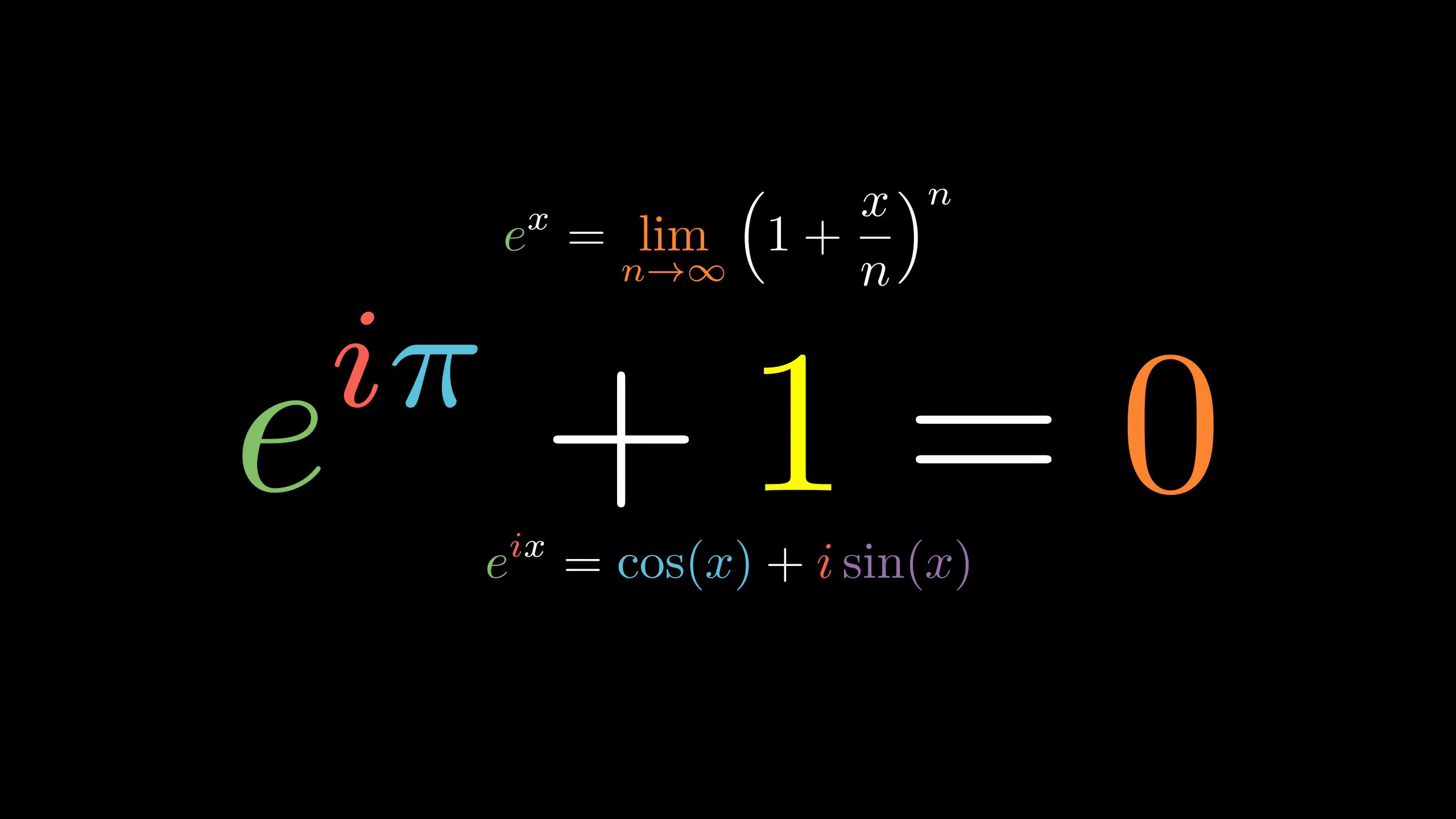
​ 图片来源：(https://zhuanlan.zhihu.com/p/106816798) 侵删

很难想象有这样一个公式，将自然底数 $e$ , 圆周率 $\pi$ , 虚数 $i$ ， 自然数 $0、1$ ，紧密地联系起来，
$$e^{i\pi }+1=0$$
这个公式从何而来？

最原始的公式发表于1748年，将三角函数与复变函数巧妙地关联了起来，
$$e^{ix}=\cos x+i\sin x$$
其中，$x$ 为弧度制单位，

令 $x=\pi$ 便得到了文章最开头的公式。

---

那么，如何理解这个公式呢 ？

---

首先，从公式自身的组成来看，包括了 $e$ , $i$ ，三角函数，指数函数，它的由来必然跳不开 自然底数 $e$ , 复数，或许还有与旋转、圆相关的一些内容，毕竟原始公式中同时存在着 $\sin x$ $\cos x$ , 且 $x$ 单位为弧度.

1. 自然底数 $e$ 的由来

$e$ 最早是在研究 “复利” 时提出的，

假如张三有单位1的本金，存入银行，银行年利率为 $r$ , 1年之后，本金+利息 $W_1=1+r$ ,

如果银行1年结算两次，即每半年结算1次，那 $W_2=(1+\frac{r}{2}{)}^2$ ,

此时，引入银行1年结算的次数 $n$ ， 那 $W_n=(1+\frac{r}{n}{)}^n$ ,

如果 $n\to \infty$ , $W_n\to \infty$ ?, 并不会，$W_n$ 会趋向于一个确定的极限，
$$\underset{n\to \infty }{\lim }(1+\frac{r}{n}{)}^n=e^r$$
而当 $r=1$ 时，便会有如下结果：
$$\underset{n\to \infty }{\lim }(1+\frac{1}{n}{)}^n=e$$

2. $i$ 复数乘法的几何意义

对一个复数：
$$a+bi$$
其中，$a$ 为实部，$b$ 为虚部，以类似极坐标的形式在复平面可以表示为：

​ 图片来源：(截图自[用几何直觉理解欧拉公式！]) 侵删

两个复数相乘实质上为：模长相乘，幅角相加

​ 图片来源：(截图自[用几何直觉理解欧拉公式！]) 侵删

3. 直面欧拉公式

前面已经给出如下公式：
$$\underset{n\to \infty }{\lim }(1+\frac{r}{n}{)}^n=e^r$$
用 $i\pi$ 替换 $r$ ，则有：
$$e^{i\pi }=\underset{n\to \infty }{\lim }(1+\frac{i\pi }{n}{)}^n$$
此时，将等式右侧看作 $n$ 项 $1+(\pi /n)i$ 的乘积，这里便会用到复数乘法的几何意义，

当 $n\to \infty$ 时， $1+(\pi /n)i$ 的幅角等于 $\pi /n$ ，$n$ 项相乘，最终幅角变为 $(\pi /n)\ast n=\pi$ ，即 $e^{i\pi }=-1$

​ 图片来源：(截图自[用几何直觉理解欧拉公式！]) 侵删

若用 $i\theta$ 替换 $r$，则有：
$$e^{i\theta }=\underset{n\to \infty }{\lim }(1+\frac{i\theta }{n}{)}^n=\cos \theta +i\sin \theta$$

---

那么，理解这样一个不算简单的公式，到底有什么用，它能用来做什么？

---

上面说了这么多，其实这部分才是对于我这样一个不研究数学的人最关心的问题。

我是这样的… 卷积神经网络–>卷积–>傅里叶变换–>欧拉公式

---

传送门

“上帝公式”(欧拉公式)真的神到无法触碰？

自然底数e怎么就“自然”了？

复数，一个充满故事又奇特的数

用几何直觉理解欧拉公式！