SGD 为什么叫“随机”梯度下降？深入剖析其真正含义！【代码实战】

随机梯度下降（SGD）中的“随机”究竟是什么意思？

在机器学习和深度学习的优化过程中，随机梯度下降（Stochastic Gradient Descent, SGD） 是一种非常重要的优化方法。然而，很多初学者都会有这样的疑问：

SGD 又叫增量梯度下降，因为它对每个样本点都进行更新。那为什么它被称为“随机”梯度下降？其中的“随机”究竟是什么意思？

这篇博客将深入剖析这个问题，并解释 SGD 相对于传统梯度下降方法的核心区别。

---

1. 经典梯度下降（GD）：完整数据集的梯度计算

在传统的 批量梯度下降（Batch Gradient Descent, BGD） 方法中，每次参数更新都需要计算整个训练集的梯度，公式如下：
$$\theta =\theta -\eta \cdot \nabla J(\theta )$$
其中：

• $\theta$ 是待优化的参数，
• $\eta$ 是学习率，
• $\nabla J(\theta )$ 是对整个数据集计算的梯度：
  $$\nabla J(\theta )=\frac{1}{m}\sum _{i=1}^m\nabla J_i(\theta )$$
  其中 $m$ 是数据集的样本数，$J_i(\theta )$ 是单个样本的损失。

问题：当数据集很大时，每次计算完整梯度的成本很高，训练速度非常慢，尤其是在深度学习任务中。

---

2. 随机梯度下降（SGD）：为什么是“随机”梯度下降？

(1) 随机抽取数据点进行更新

SGD 采用了一种更高效的策略：每次参数更新时，仅使用一个样本点的梯度，而不是整个数据集，计算公式如下：

$$\theta =\theta -\eta \cdot \nabla J_i(\theta )$$

其中 $i$ 是当前随机选取的样本索引。

这样，SGD 每次迭代不需要计算所有数据的梯度，而是仅使用一个样本进行参数更新，从而显著降低计算开销，提高训练速度。

(2) 随机打乱数据集，避免顺序影响

在实际实现 SGD 时，通常会在每个 epoch 之前对数据集进行随机打乱（shuffle），确保：

• 数据不会按照固定顺序训练，避免模型陷入局部最优。
• 训练的样本是无序的，使得更新方向不会受到数据排序的影响。

这就是“随机”梯度下降的 关键 ：样本点是 随机选择 的，而不是按照顺序逐个更新。

---

3. SGD 相比批量梯度下降的优缺点

方法	每次计算的梯度	计算开销	更新速度	是否震荡
批量梯度下降（BGD）	所有样本的梯度	高	慢	无震荡
随机梯度下降（SGD）	一个样本的梯度	低	快	有较大震荡
小批量梯度下降（MBGD）	一小批样本的梯度	适中	适中	震荡较小

总结：

• BGD 计算精确，但计算量大，不适合大规模数据。
• SGD 计算快，但梯度波动大，容易震荡。
• 小批量梯度下降（MBGD） 在计算效率和稳定性之间取得平衡，最常用。

---

4. 解决 SGD 震荡问题的优化策略

由于 SGD 仅基于单个样本进行更新，因此梯度的方向会有较大的随机波动，容易导致参数来回震荡。为了缓解这个问题，通常会使用以下优化策略：

1. 动量方法（Momentum）：通过引入“惯性”，在更新时保留一部分之前的梯度方向，使得更新更平滑。
2. 自适应学习率方法（Adam、RMSProp）：自动调整学习率，使得收敛更加稳定。
3. 学习率衰减（Learning Rate Decay）：随着训练进行逐步降低学习率，让模型在训练后期更稳定地收敛。

---

5. 总结

SGD 为什么被称为“随机”梯度下降？

• 关键原因：SGD 在每次参数更新时，只随机选择一个样本点来计算梯度，而不是使用整个数据集。
• 进一步优化：为了防止数据的固定顺序影响模型，SGD 还会对训练数据进行随机打乱（shuffle），确保更新方向的随机性。
• 优缺点：
  • 优点：计算高效，适合大规模数据。
  • 缺点：梯度波动大，容易震荡，但可以通过优化方法改善。

在实际应用中，SGD 的随机性不仅加快了训练速度，还能帮助模型跳出局部最优，使其成为深度学习优化的核心方法之一。

6. 代码实现：逐步理解 SGD

为了更直观地理解随机梯度下降（SGD），我们将用 Python 从零开始实现 批量梯度下降（BGD） 和 随机梯度下降（SGD），并对比它们的收敛效果。我们以一个简单的线性回归问题为例：

6.1 生成数据集

首先，我们创建一个简单的线性数据集：
$$y=3x+2+ϵ$$
其中 $ϵ$ 是一些随机噪声。

import numpy as np
import matplotlib.pyplot as plt

# 生成 100 个数据点
np.random.seed(42)
X = 2 * np.random.rand(100, 1)  # 生成随机输入 x
y = 3 * X + 2 + np.random.randn(100, 1) * 0.5  # 线性关系 y = 3x + 2 + 噪声

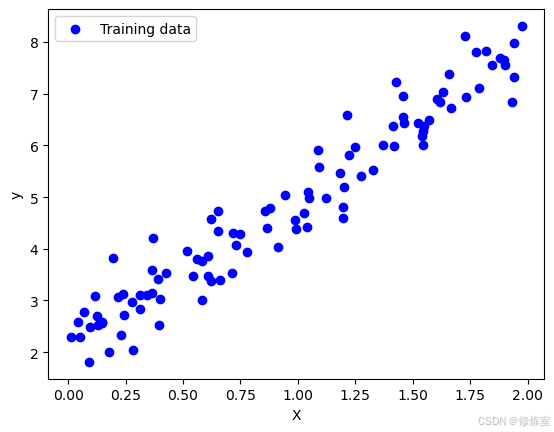
# 绘制数据分布
plt.scatter(X, y, color='blue', label="Training data")
plt.xlabel("X")
plt.ylabel("y")
plt.legend()
plt.show()

---

6.2 批量梯度下降（BGD）

在批量梯度下降（Batch Gradient Descent）中，我们使用所有样本计算梯度，然后更新参数。
公式如下：
$$\theta =\theta -\eta \cdot \frac{1}{m}\sum _{i=1}^m\nabla J_i(\theta )$$
其中 $\theta$ 是待优化参数，$\eta$ 是学习率，$m$ 是样本数。

# 批量梯度下降（BGD）实现
def batch_gradient_descent(X, y, learning_rate=0.1, n_iters=1000):
    m = len(X)
    theta = np.random.randn(2, 1)  # 初始化参数 [w, b]
    
    X_b = np.c_[np.ones((m, 1)), X]  # 添加偏置项
    loss_history = []

    for iteration in range(n_iters):
        gradients = (2 / m) * X_b.T @ (X_b @ theta - y)  # 计算全局梯度
        theta -= learning_rate * gradients  # 更新参数
        loss = np.mean((X_b @ theta - y) ** 2)  # 计算损失
        loss_history.append(loss)

    return theta, loss_history

theta_bgd, loss_bgd = batch_gradient_descent(X, y)
print(f"BGD 训练结果: theta = {theta_bgd.ravel()}")

在你的 批量梯度下降（BGD） 代码中，theta 是线性回归模型的参数，包括权重 w 和偏置 b，最终的 theta 由梯度下降迭代计算得出。

theta 具体代表什么？

代码中初始化了：

theta = np.random.randn(2, 1)  # 初始化参数 [w, b]

这意味着 theta 是一个 2×1 的列向量，其中：

• theta[0] 代表 偏置项 b
• theta[1] 代表 权重 w（即特征 X 的系数）

在 batch_gradient_descent 过程中，每次迭代都会基于均方误差（MSE） 计算梯度，并更新 theta，最终收敛到一个最优解。

如何查看 theta 的最终值？

代码在最终打印：

print(f"BGD 训练结果: theta = {theta_bgd.ravel()}")

theta_bgd.ravel() 将 theta 拉平成一维数组，假设结果如下：

BGD 训练结果: theta =  [2.10754808 2.88505669]

则模型的最终方程为：

$$\hat{y}=2.88X+2.10$$
这表示：

• b ≈ 2.10，即当 X=0 时，预测值 y 约为 2.10。
• w ≈ 2.88，即 X 每增加 1，预测 y 增加 2.88。

---

6.3 随机梯度下降（SGD）

在 SGD 中，我们随机选取一个样本计算梯度，并更新参数：
$$\theta =\theta -\eta \cdot \nabla J_i(\theta )$$
我们还需要对数据进行随机打乱，避免数据的固定顺序影响模型的收敛。

# 随机梯度下降（SGD）实现
def stochastic_gradient_descent(X, y, learning_rate=0.1, n_epochs=1000):
    m = len(X)
    theta = np.random.randn(2, 1)  # 初始化参数 [w, b]
    
    X_b = np.c_[np.ones((m, 1)), X]  # 添加偏置项
    loss_history = []

    for epoch in range(n_epochs):
        indices = np.random.permutation(m)  # 随机打乱数据
        for i in indices:
            xi = X_b[i:i+1]  # 取单个样本
            yi = y[i:i+1]
            gradients = 2 * xi.T @ (xi @ theta - yi)  # 计算梯度
            theta -= learning_rate * gradients  # 更新参数
            
        loss = np.mean((X_b @ theta - y) ** 2)  # 计算损失
        loss_history.append(loss)

    return theta, loss_history

theta_sgd, loss_sgd = stochastic_gradient_descent(X, y)
print(f"SGD 训练结果: theta = {theta_sgd.ravel()}")

模型的最终方程为：

$$\hat{y}=2.78X+2.30$$
这表示：

• b ≈ 2.30，即当 X=0 时，预测值 y 约为 2.30。
• w ≈ 2.78，即 X 每增加 1，预测 y 增加 2.78。

---

6.4 训练过程对比

我们绘制 BGD 和 SGD 在训练过程中的损失下降情况：

plt.plot(loss_bgd, label="BGD Loss")
plt.plot(loss_sgd, label="SGD Loss")
plt.xlabel("Iteration (Epoch for SGD)")
plt.ylabel("Loss")
plt.legend()
plt.title("BGD vs SGD Loss Curve")
plt.show()

6.5 观察 SGD 的随机性

我们多次运行 SGD，并观察每次拟合出的参数值是否一致：

for i in range(5):
    theta_sgd, _ = stochastic_gradient_descent(X, y)
    print(f"Run {i+1}: SGD theta = {theta_sgd.ravel()}")

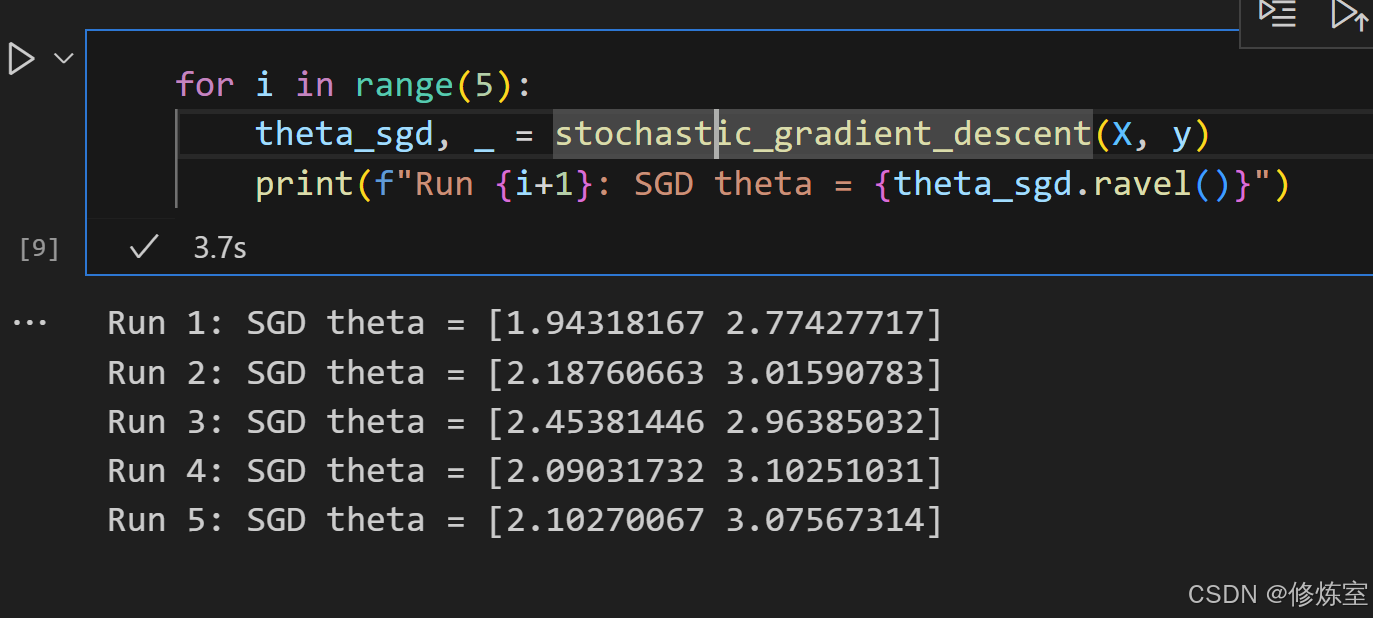
你会发现，由于 SGD 每次更新都基于随机样本，最终拟合出的参数会有细微差异，这就是 SGD 的随机性 所在！

---

7. 总结

• 批量梯度下降（BGD） 使用所有数据计算梯度，更新稳定，但计算量大。
• 随机梯度下降（SGD） 每次使用单个样本计算梯度，计算高效，但参数更新方向会有较大波动。
• SGD 的“随机”性来源于：
  1. 每次迭代随机选择样本 进行梯度计算。
  2. 在每个 epoch 前对数据随机打乱，避免样本顺序影响学习过程。
• SGD 适用于大规模数据集，收敛更快，但需要优化方法（如动量、Adam）来减少震荡。