Transformer 模型介绍（六）——残差连接、线性层与损失函数

夜幕龙

已于 2025-02-23 11:59:11 修改

阅读量899

点赞数 14

分类专栏：具身智能算法基础文章标签： transformer 深度学习人工智能

于 2025-02-23 11:53:11 首次发布

本文链接：https://blog.csdn.net/qq_28912651/article/details/145662007

版权

具身智能算法基础专栏收录该内容

15 篇文章

订阅专栏

在深度神经网络中，随着网络层数的增加，模型的性能可能会出现不升反降的现象，这就是网络退化（Network Degradation）问题。具体而言，当网络过深时，模型的训练会变得非常困难，准确率可能在达到某个峰值之后迅速下降，这通常是由于梯度消失或梯度爆炸造成的

残差连接（Residual Connection）的提出正是为了解决这一问题。ResNet（Residual Networks）通过引入残差连接，能够有效避免梯度消失和梯度爆炸问题，同时确保网络的深度不会影响到模型的表现

1 残差连接 Residual Connection

1.1 定义

1.2 Transformer中的残差连接

1 残差连接 Residual Connection

1.1 定义

残差连接的核心思想是跳跃连接，即直接将某一层的输入 x 加上其输出 f(x)，并作为该层的最终输出。这样，即使网络变得非常深，网络的效果也不会比浅层网络差

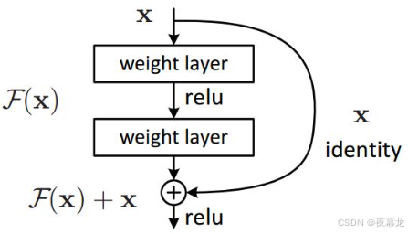
简言之，残差连接通过保持信息流动，使得网络更容易训练，并能在深层网络中保持较好的性能

$\text{Output} = x + f(x)$

这种结构的优势在于，它能够帮助网络保持稳定的梯度流动，避免深层网络的退化问题

1.2 Transformer中的残差连接

Transformer 模型中的编码器和解码器都使用了层标准化+残差连接的组合。这种结构的核心思想是，在每个子层之后，先进行层标准化，然后再通过残差连接进行处理。具体而言：

编码器部分在经过自注意力层和前馈神经网络之后，都会分别进行层标准化和残差连接。这种设计确保了每一层的输出能够稳定传递，并避免了梯度消失或爆炸的问题
解码器部分则分为三个部分：自注意力层、编码器-解码器注意力层和前馈神经网络，每一部分之后都会经过层标准化和残差连接

2 线性层与Softmax层

在 Transformer 模型中，解码器的最终输出是一个浮点向量，但我们希望将这个输出转换为一个词元（Token），即模型最终生成的单词。为此，Transformer 模型使用了一个线性层，该层是一个全连接神经网络，它将解码器的输出向量投影到一个更高维度的向量空间中，称为 logits 向量。logits 向量的维度与词汇表的大小一致，其中每个元素代表了该词元的得分

接下来，需要将这个 logits 向量转化为概率分布，以便选择最有可能的词元。为此，使用了Softmax 层。Softmax 函数将 logits 向量中的每个得分转化为概率值，确保所有概率之和为1。具体地，Softmax函数的计算公式如下：

$P(y_i) = \frac{e^{z_i}}{\sum_{j} e^{z_j}}$

其中，zi 是 logits 向量中的第 i 个元素，表示第 i 个词元的得分

Softmax 层将这些得分转化为概率，最后通过选择概率最大的元素，来决定该时间步的输出词元

3 损失函数与模型训练

3.1 损失函数

在 Transformer 模型的训练过程中，我们需要一种损失函数来衡量模型的输出与真实标签之间的差异。比较两个概率分布的最常见方法是计算它们的交叉熵（Cross-Entropy）或KL散度（Kullback-Leibler Divergence）。这两者的目标是通过量化预测概率分布与目标分布的差距，帮助模型调整参数，从而逐渐优化预测结果