自动控制原理【2021/12/19更新】

写在前面

参考：
[1] Modern Control Systems, Dorf and Bishop
[2] 自动控制原理，胡寿松

(一) 控制系统导论

系统框图的绘制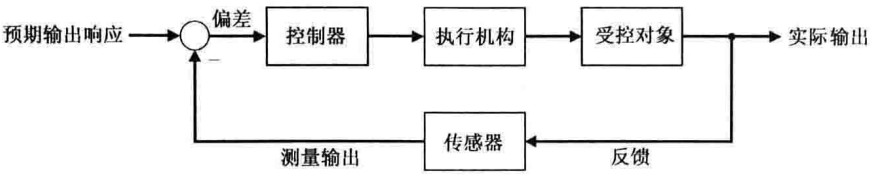
需要能够对一个控制系统绘制出相应的框图。（把每一部分找清楚，箭头上对应的是物理量）
大部分控制系统无非是为了跟踪输入，或是抑制扰动。

(二) 系统数学模型

(1) 微分方程

需要掌握一些基础知识：电路、电机等
注：胡寿松《自动控制原理》（第七版）P28运放我看不懂。

(2) 传递函数

线性系统的传递函数：当两个变量的初值都假定为零时，输出变量的拉普拉斯变换与输入变量的拉普拉斯变换之比。
初值定理：${\lim }_{t\to 0^{+}}y(t)={\lim }_{s\to \infty }sY(s)$ （比如：我们可以用来求$y^{\prime }(0)$）
终值定理：${\lim }_{t\to \infty }y(t)={\lim }_{s\to 0}sY(s)$

(3) 方框图

方框图的绘制与简化

(4) 信号流图

信号流图只适用于线性系统，方框图也可用于非线性系统。
梅森增益公式: $$T=\frac{{\sum }_k{P}_k{\Delta }_k}{\Delta }$$$$\Delta =1-\sum _{n=1}^N{L}_n+\sum _{n,m不接触回路}{L}_n{L}_m-\cdots$$回路：起点和终点在同一节点，而且信号通过每一节点不多于一次的闭合通路。
不接触回路：回路之间没有公共节点。
例1：求$y_7/y_3$
例2：求$y_6/y_1$（注意：不要漏掉回路）

(三) 反馈控制系统的特性与性能

(1) 误差信号

误差信号$$E\left(s\right)=R\left(s\right)-Y\left(s\right)$$
$$E\left(s\right)=\frac{1}{1+L\left(s\right)}R\left(s\right)-\frac{G\left(s\right)}{1+L\left(s\right)}{T}_d\left(s\right)+\frac{L\left(s\right)}{1+L\left(s\right)}N\left(s\right)$$

对于非单位负反馈系统，等效单位负反馈系统的开环传递函数$Z\left(s\right)$为$$Z\left(s\right)=\frac{L\left(s\right)}{1+L\left(s\right)(H\left(s\right)-1)}$$我们可以得到非单位负反馈系统的误差常数为$K_p={\lim }_{s\to 0}Z\left(s\right)$,$K_v={\lim }_{s\to 0}sZ\left(s\right)$,$K_a={\lim }_{s\to 0}{s}^{2}Z\left(s\right)$

(2) 二阶系统性能

$$T_s=\frac{4}{\zeta {\omega }_n}$$$$T_p=\frac{\pi }{{\omega }_n\sqrt{1-{\zeta }^2}}$$$$M_{pt}=1+e^{\frac{-\zeta \pi }{\sqrt{1-{\zeta }^2}}}$$$$P.O.=100e^{\frac{-\zeta \pi }{\sqrt{1-{\zeta }^2}}}$$$$T_{r_1}=\frac{2.16\zeta +0.60}{{\omega }_n}\left(0.3⩽\zeta ⩽0.8\right)$$$$t_r=\frac{\pi -\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{c}\mathrm{o}\mathrm{s}\zeta }{{\omega }_n\sqrt{1-{\zeta }^2}}$$
频域性能指标
谐振峰值$M_r$是频率响应的最大值，它出现在谐振频率${\omega }_r$处。
带宽${\omega }_B$定义为在幅频特性曲线上，对数幅值增益从低频值下降3$dB$时所对应的频率。在通常情况下，系统带宽与系统的阶跃响应速度成正比，与调节时间成反比。
剪切频率越大，时间响应越快。
$$M_r=\frac{1}{2\zeta \sqrt{1-{\zeta }^2}}$$$${\omega }_r={\omega }_n\sqrt{1-2{\zeta }^2}$$$${\omega }_b={\omega }_n\sqrt{1-2{\zeta }^2+\sqrt{2-4{\zeta }^2+4{\zeta }^4}}$$$${\omega }_c={\omega }_n\sqrt{\sqrt{1+4{\zeta }^4}-2{\zeta }^2}$$$$\gamma =arc\tan \frac{2\zeta }{\sqrt{\sqrt{1+4{\zeta }^4}-2{\zeta }^2}}$$
高阶系统$$M_r=\frac{1}{\left|\sin \gamma \right|}$$$$\sigma =0.16+0.4(M_r-1),1⩽M_r⩽1.8$$$$t_s=\frac{K_0\pi }{{\omega }_c}(\Delta =5\%),K_0=2+1.5(M_r-1)+2.5{(M_r-1)}^2$$

(3) 零点和第三个极点对二阶系统响应的影响

3.1 第三个极点

$$T\left(s\right)=\frac{1}{\left(s^2+0.9s+1\right)\left(\gamma s+1\right)}$$

3.2 零点

$$T\left(s\right)=\frac{\left(\frac{{\omega }_n^2}{a}\right)\left(s+a\right)}{s^2+0.9{\omega }_{n}s+{\omega }_n^2}$$

(4) *线性系统的简化

原系统$G_H(s)=K\frac{a_m{s}^m+...+a_{1}s+1}{b_n{s}^n+...+b_{1}s+1}$
近似的低阶系统$G_L(s)=K\frac{c_p{s}^p+...+c_{1}s+1}{d_g{s}^g+...+d_{1}s+1}$
$M_{2q}={\Delta }_{2q}$，$q=1,2,...$其中$M_{2q}={\sum }_{k=0}^{2q}\frac{{(-1)}^{k+q}{M}^{(k)}(0)M^{(2q-k)}(0)}{k!(2q-k)!}$，类似定义${\Delta }_{2q}$
例子见书5.9


原系统：$t_r=2.74s$，$t_s=5s$

近似系统：$t_r=2.75s$，$t_s=4.82s$
课本写的是不太合适的，用欠阻尼系统的近似公式估算一个过阻尼系统。

(四) 劳斯判据

(1) 内容

对特征方程$a_n{s}^n+a_{n-1}{s}^{n-1}+\cdots +a_{1}s+a_0=0$，正实部根的个数等于劳斯判定表第一列元素的正负符号的变化次数。

(2) 特殊情况

2.1 首列中出现零元素，所在行存在非零元素

可用$\epsilon$代替零元素参与计算或用因子$\left(s+a\right)$乘以原特征方程

2.2 出现全零行

特征根关于零点对称时会出现这种情况。可用上一行的系数构造辅助方程$F\left(s\right)=0$，并将方程对s求导，使用所得导数方程的系数。

2.3 虚轴上有重根

如果在虚轴上的共轭根是重根，则系统是不稳定的，而劳斯判据不能发现这种不稳定。

(3) 相对稳定性

(五) 根轨迹

(1) 步骤

(2) 零度根轨迹

(3) 开环零极点影响

增加开环极点，将多一条发散轨迹，该轨迹对原有轨迹有排斥作用，系统稳定性变差。
增加开环零点，将少一条发散轨迹，系统稳定性变好。

(4) 根轨迹簇

研究多个参数对系统的影响。考虑特征方程$s^3+3s^2+2s+\beta s+\alpha =0$。先令$\beta =0$，绘制根轨迹，在所得根轨迹上，找到$\alpha$为特定值时对应的根，然后绘制关于$\beta$的根轨迹。

(六) 频率响应法

(1) 频率响应

系统的频率响应：系统对正弦输入信号的稳态响应。$y\left(t\right)=A\left|T\left(j\omega \right)\right|\sin \left(\omega t+\varphi \right)$

(2) 极坐标图

(3) 波特图

所有零点都在s平面左半平面的传递函数称为最小相位传递函数。

(4) 对数幅相图

(七) 频域稳定性

(1) 奈奎斯特稳定性判据

闭环反馈控制系统稳定的充要条件是$L(s)$在$s$平面上的映射像围线${\tau }_L$沿逆时针方向包围$(-1,0)$点的周数，等于$L(s)$在$s$右半平面内极点的个数。

(2) 相对稳定性

幅值裕度，相角裕度$$\zeta =0.01\gamma$$

(3) 尼科尔斯图

(4) 时延系统

(八) 反馈控制系统设计

(1) 波特图设计超前校正

1.根据稳态误差，确定开环增益
2.计算待校正系统的相角裕度
3.计算所需添加的超前相角，$\sin {\phi }_m=\frac{a-1}{a+1}$计算$a$
4.计算$10loga$,在待校正系统的幅频特性曲线上确定与$-10logadB$对应的频率，即为${\omega }_c$同时也是${\omega }_m$
5.计算$p={\omega }_m\sqrt{a},z=p/a$，确认相角裕度是否满足，若不满足，则重复

(2) 根轨迹设计超前校正

1.根据系统性能指标，计算主导极点的预期位置
2.绘制待校正系统的根轨迹
3.先将超前校正网络零点直接配置在预期主导极点下方（或在前两个开环极点的左侧近旁）
4.配置超前校正网络的极点，使得在预期主导极点处，满足相角要求
5.在预期主导极点处，确定系统总增益，计算系统稳态误差常数是否满足，若不满足，则重复

(3) 根轨迹设计滞后校正

1.根据系统性能指标，计算主导极点的预期位置
2.绘制待校正系统的根轨迹
3.根据预期主导极点，确定待校正系统的增益，并计算此时的稳态误差常数
4.比较矫正前后的稳态误差常数，计算所需的增益放大倍数，即为校正网络零极点幅值之比，配置零极点在靠近原点的地方

(4) 波特图设计滞后校正

1.根据稳态误差，确定待校正系统增益，绘制波特图
2.计算待校正系统的相角裕度
3.确定能够满足相角裕度要求的穿越频率${\omega }_c$，可以预留$5°$
4.配置零点应比穿越频率小十倍频程，即$\frac{1}{bT}=0.1{\omega }_c^{\prime \prime }$
5.根据增益$-20logb$计算参数$b$

(5) 波特图设计超前滞后校正

1.根据稳态误差，确定开环增益
2.绘制波特图，确定${\omega }_c$，$\gamma$，$h$
3.选择斜率从$-20$变为$-40$的频率为超前部分的交接频率${\omega }_b$
4.根据系统特性要求选取${\omega }_c^{\prime }$，$20lg\alpha =L({\omega }_c^{\prime })+20lg({\omega }_c^{\prime }/{\omega }_b)$得出$\alpha$
5.根据相角裕度估算${\omega }_a$
6.检验已校正系统的各项性能指标

(5) 根轨迹设计超前滞后校正

1.根轨迹设计超前校正
2.根轨迹设计滞后校正

(6) 最小节拍响应系统设计

最小节拍响应：既能具有最小的超调量，又有快速到达稳态响应的允许波动范围，并且能够持续保持在该波动范围之内的时间响应。

(7) 一些例子

例1

$G_c(s)=\frac{30s+300}{s}$，$G_p(s)=10$

例2 $G(s)=\frac{40}{s^2(s+40)}$，设计合适的校正网络，使得系统足够稳定，超调量在$10\%$到$20\%$之间，调节时间不大于$2s$(按$2\%标准$)

主要是要抵消闭环零点对系统性能指标的影响。
例3 $G(s)=K_a\frac{3.75}{(s+0.15)(0.15s+1)}$，设计合适的$PI$控制器，使得系统稳态误差为零，超调量为$10\%$，调节时间小于$1.5s$(按$2\%标准$)。若采用超前校正网络，重新完成，并比较结果。

PI	超前

设计$PI$控制器时，答案中如何取到$a=0.2$的呢？事实上，我们为使得系统的特性与主导极点的特性接近，可以将闭环系统多出的一对零极点设计非常接近。对于$G_c(s)G(s)=\frac{25K(s+a)}{s(s+0.15)(s+6.67)}$，其特征方程为$s^3+6.82s^2+(25K+1)s+25Ka=0$。令$(s+a)$为该特征方程的一个因式，即$s=-a$为特征方程的解，得$-a^3+6.82a^2-(25K+1)a+25Ka=0$，解得$a=0.15$或$a=6.67$。注意到$s^3+6.82s^2+(25K+1)s+25Ka=(s+a)(s^2+2\zeta {\omega }_n+w_n^2)$，展开可知$2\zeta {\omega }_n+a=6.82$，我们取$a=0.15$，进一步可以求得$K=1.278，\zeta {\omega }_n=3.335$。

例4 $G(s)=\frac{5000}{s(s+20)(s+5)}$，设计校正网络，使得$K_v>40$，$\zeta =0.7$

注意根轨迹图。

例5


对于开环波特图，对应在$\omega =6$时幅值最大
例6 $G(s)=\frac{K}{s(s/2+1)(s/6+1)}$，用两个完全相同的一阶超前校正网络串联起来，实现对系统的二阶校正，使得$K_v=20$，相角裕度为$45°$，闭环带宽大于$4rad/s$。

例7 $G(s)=e^{-s/2}$，试设计一个合适的$G_c(s)$，使阶跃响应稳态误差小于$2\%$，相角裕度$30°$，计算校正后带宽。

(九) 数字控制系统

(1) 典型结构图

(2) $z$域传递函数

2.1 零阶保持器

$$G(s)=G_0(s)G_p(s)$$ G ( z ) = Z { G ( s ) } = ( 1 − z − 1 ) Z ( G p ( s ) s ) G(z)=Z\{G(s)\}=(1-z^{-1})Z(\frac{G_p(s)}s) G(z)=Z{G(s)}=(1−z−1)Z(sGp​(s)​)

2.2 串联环节之间有采样开关

$$D(z)=G_1(z)G_2(z)$$

2.3 串联环节之间无采样开关

$$D(z)=G_1{G}_2(z)$$

2.4 闭环系统计算

1.选取中间变量，该中间变量为某一采样开关的输出
2.建立等式，化简，消去中间变量
以下图为例，选取$E_1^{\ast }(s)$，$E_1(z)=R{G}_1(z)-E_1(z)G2HG1(z)$，可得，$E_1(z)=\frac{R{G}_1(z)}{1+G_{2}H{G}_1(z)}$，代入$C(z)=E_1(z)G_2(z)$，即得$C(z)=\frac{R{G}_1(z)G_2(z)}{1+G_{2}H{G}_1(z)}$

2.5 稳态误差

$e_{ss}(\infty )={\lim }_{z\to 1}(1-z^{-1})E(z)$

(3) 稳定性

令$z=\frac{w+1}{w-1}$，根据劳斯判据判断稳定性

(4) 控制器设计

设计$G_c(s)=K\frac{s+a}{s+b}$，转换成$D(z)=C\frac{z-A}{z-B}$，$A=e^{-aT}B=e^{-bT}C\frac{1-A}{1-B}=K\frac{a}{b}$

(5) $PID$数字控制器的实现

在$s$域中，$\frac{U(s)}{X(s)}=G_c(s)=K_{p}s+\frac{K_I}{s}+K_{D}s$，求对应的离散$PID$控制器
对于微分，$u(kT)=\frac{1}{T}(x(kT)-x((k-1)T))$，$U(z)=\frac{1-z^{-1}}{T}X(z)=\frac{z-1}{Tz}X(z)$
对于积分，$u(kT)=u((k-1)T)+Tx(kT)$，$U(z)=z^{-1}U(z)+TX(z)$，$\frac{U(z)}{X(z)}=\frac{Tz}{z-1}$
从而，$G_c(z)=K_P+\frac{K_{I}Tz}{z-1}+K_D\frac{z-1}{Tz}$

(十) 线性系统的状态空间分析与综合

(1) 标准型

(2) 可控性、可观性

(3) 极点配置、状态观测器

(4) 离散时间系统

$$G(T)=e^{AT}$$$$H(T)=({\int }_0^T{e}^{A\lambda }d\lambda )B$$

(十一) 非线性系统

(1) 非线性系统概述

1.1 典型非线性环节

继电特性 产生振荡
死区特性 存在稳态误差
饱和特性
间隙特性

1.2 非线性系统的特点

多孤立平衡点
极限环、自激振荡
混沌
分岔
不仅含有同频率，还含有高次谐波分量
有限逃逸时间

(2) 描述函数法

2.1 应用条件

非线性系统的结构图可简化成一个非线性环节$N$和一个线性部分$G(s)$串联的闭环结构。（本身具有或者能通过转换）
$N(A)$奇对称，基波幅值占优。
非线性 时不变。
系统的线性部分具有良好的低通滤波特性。

2.2 描述函数

$N(X,\omega )=\frac{B_1+j{A}_1}{X}$

2.3 非线性特性的串并联

2.4 稳定性分析

a.若$G(j\omega )$不包围$-\frac{1}{N}$$\Rightarrow$稳定
b.若$G(j\omega )$与$-\frac{1}{N}相交$$\Rightarrow$临界稳定
进一步，分析极限环的稳定性
c.若$G(j\omega )$包围$-\frac{1}{N}$$\Rightarrow$不稳定

2.5 极限环分析

$-\frac{1}{N(A)}$与$G_p(s)$实部、虚部分别相等
例：分析$\ddot{x}+\dot{x}=\{\begin{array}{l}1,\dot{x}-x>0\\ -1,\dot{x}-x<0\end{array}$系统的极限环
先把系统表示成分线性部分和线性部分，进一步再分析（结果$X=\frac{2\sqrt{2}}{\pi }$）

2.6 描述函数法的准确性

当$-\frac{1}{N(A)}$与$G_p(s)$越接近垂直时，得到的结果越准确
描述函数法对于正弦输入的准确性更高
描述函数法的难度和准确性只取决于非线性部分

(3) 相平面法

3.1 相轨迹

$\ddot{x}+f(x,\dot{x})=0\Rightarrow \frac{d\dot{x}}{dx}=\frac{-f(x,\dot{x})}{\dot{x}}$
相轨迹的绘制：解析法、等倾线法

3.2 二阶线性系统的相轨迹

焦点 节点 中心点 鞍点

3.3 奇点

(4) 李雅普诺夫稳定性

4.1 定义

对于平衡点$x=0$，我们有：
李雅普诺夫稳定：$\forall R>0,\exists r>0,\Vert x(0)\Vert <r\Rightarrow \forall t\ge 0,\Vert x(t)\Vert <R$
渐近稳定：李雅普诺夫稳定，且$\exists r>0,\Vert x(0)\Vert <r\Rightarrow {\lim }_{t\to \infty }x(t)=0$
指数稳定：$\exists \alpha >0,\lambda >0,\forall t>0,\Vert x(t)\Vert ⩽\alpha \Vert x(0)\Vert e^{-\lambda t}$
如果对于任意的初始状态，渐进稳定或指数稳定的条件成立，那么我们称为全局渐近稳定或全局指数稳定。

4.2 李雅普诺夫线性化方法

李雅普诺夫第一方法、间接法

4.3 李雅普诺夫直接法

李雅普诺夫第二方法
系统的李雅普诺夫函数：$V(x)>0,\dot{V}(x)⩽0$

(十二) 一些tips

1.

答案所给的框图中的积分环节应该缺少了一个系数。
分析整个系统时，可以从偏差信号开始。

2.为使用奈氏判据等判断系统稳定性时，我们可以将传递函数转化成一些更容易操作的函数。（保证闭环特征方程不变）
3. 传递函数的约分 不约分
4. 如$x^3$，求描述函数时，可以直接算输出并取基次谐波，除以输入。
5.中频段以$-20dB/dec$穿越$0dB$线，稳定 但若$-60dB/dec$转到$-20dB/dec$也不稳定。
6.$PD$控制器产生有效的早期修正信号，增加系统的阻尼程度，提高系统的响应速度，提高系统的稳定性。但会放大高频信号，系统抗干扰能力减弱。
$PI$控制器提高系统的型别，提高系统的精度，系统跟踪能力增强，系统的稳定性下降。
7.系统的脉冲响应反映了系统的静特性，系统的动特性可以用正弦信号响应来反映。
8.考虑稳态误差前，先判断稳定性。
9.一道有一定计算的题目
设单位负反馈系统的开环传递函数为$G(s)=\frac{{{\omega }_n}^2}{s(s+2\zeta {\omega }_n)}$，已知闭环频率特性的模$|\varphi (j2)|=\frac{1}{2\zeta }$，相角裕度为$\gamma =26.56°$。试求输入$r(t)=3sin4t$时，系统的稳态输出。
答案：${\omega }_n=2$，$\zeta =0.236$，$c_{\infty }(t)=0.954sin(4t-162.5°)$
10.闭环实数零极点。零点减小系统阻尼，峰值时间提前，超调量增大；极点增大系统阻尼，峰值时间滞后，超调量减小。
11.线性定常系统的李雅普诺夫稳定性分析
$A^{T}P+PA=-Q$，$G^{T}PG-P=-Q$
12.增加实极点，调节时间的变化不确定。如本文3.1。绝对值越小，超调减少越明显。
13.如果考试用计算器算时，注意一下弧度制、角度制。
14.PID定性影响
15.求稳态误差前，先判断稳定性

16.1个根轨迹
17.波特图通过实际值确定传递函数
$0<\zeta <\frac{\sqrt{2}}{2},M_r=\frac{1}{2\zeta \sqrt{1-{\zeta }^2}}$
$\frac{\sqrt{2}}{2}<\zeta <1,M_r=2\zeta \sqrt{1-{\zeta }^2}$
${\omega }_r={\omega }_n\sqrt{1-2{\zeta }^2}$
18.对于二阶系统来说，增加开环零点，会增大系统阻尼。对于高阶系统，可能减小系统阻尼。
19.低频段决定了系统的稳态性能，中频段决定了系统的动态性能，高频段决定了系统的抗扰性能