PCA算法原理，基于PCA算法原理，应用SVD算法求取点云法向量

导言

PCA算法和SVD算法作为非常基础的算法，使用这两个算法是非常简单的，直接调用一个函数就可以了，但学习从未曾是这样。

这篇博客会详细讲解PCA的原理（自己的理解），同时基于PCA算法的原理，应用SVD算法求取点云目标的法向量。

也不敢说这篇博客写的多么的权威，但至少，我的女朋友是可以看懂的，下面开始。

声明

听说很多瞎转载，乱复制，不管公式的编写，所以全文不许转载，不然就收费一元（估计收费了没人看）

内容说明

• 博客内容：抄袭其他博客（80%-重要），加上自己整理和理解（20%-关键）。
• 代码内容：抄袭github（99%-重要），加上自己整理和理解（1%-关键）。

结论说明

使用SVD求解点云法向量的时候，需要用到这个结论：

• 点云协方差矩阵最大特征值对应的特征向量$v_1$，其方向为数据分布方差最大的方向；

• 协方差矩阵第二大特征值对应的特征向量$v_2$，其方向是与特征向量$v1$垂直方向上数据方差最大的方向；

• 协方差矩阵第三大特征值对应的特征向量$v_3$，其方向是垂直于特征向量$v1$和特征向量$v2$形成的平面的方向上数据方差最大的方向，以此类推。
  
  所以很明显，我们想求点云的法向量，只需要找到协方差矩阵对应的第三大特征值对应的特征向量就行。（估计这里会蒙，什么协方差矩阵，谁的协方差矩阵。。。）

如果只是想求解点云的法向量，这里基本就结束了，下面的原理介绍就可以不用看了。

代码在下面，数据在百度云，记住上面的结论，点赞评论666然后关注我，就可以走了。（记得看一下代码）

提取码：j75z

# -*- coding: utf-8 -*-
# @Time    : 2023-03-14
# @Author  : lab
# @desc    :
import numpy as np

def load_pc_np(filename):
    pc_source = np.load(filename)
    numPoints = len(pc_source)
    pointCloudSource = []
    row = []
    for i in range(numPoints):
        for j in range(3):
            row.append(pc_source[i][j])
        pointCloudSource.append(np.matrix([float(x) for x in row]).T)
        row = []
    return pointCloudSource


def getNeighbors(pq, pc):
    k = 8
    neighbors = []
    for i in range(len(pc)):
        dist = np.linalg.norm(pq - pc[i])
        if dist <= 0.05:
            neighbors.append((dist, i))
    neighbors.sort(key=lambda x: x[0])
    # ------------------------------------------------------------------------------------------------------------------
    # 不要自己，然后取出前k个最近点
    # ------------------------------------------------------------------------------------------------------------------
    neighbors.pop(0)
    return neighbors[:k]


def convert_pc_to_matrix(pc):
    numpy_pc = np.matrix(np.zeros((3, len(pc))))
    for index, pt in enumerate(pc):
        numpy_pc[0:3, index] = pt
    return numpy_pc


source_pc = load_pc_np('data/plant_source.npy')
# ----------------------------------------------------------------------------------------------------------------------
# 查找第0个点的领域
# ----------------------------------------------------------------------------------------------------------------------
indN = getNeighbors(source_pc[0], source_pc)
indN = [indN[i][1] for i in range(len(indN))]
# ----------------------------------------------------------------------------------------------------------------------
# 取出局部领域三维点信息
# ----------------------------------------------------------------------------------------------------------------------
X = convert_pc_to_matrix(source_pc)[:, indN]
X = X - np.mean(X, axis=1)
# ----------------------------------------------------------------------------------------------------------------------
# 计算3×3的协方差矩阵，XYZ三个变量
# ----------------------------------------------------------------------------------------------------------------------
cov = np.matmul(X, X.T) / (len(indN) - 1)
_, _, Vt = np.linalg.svd(cov)
normal = Vt[2, :]

PCA算法原理

看PCA算法原理的时候，看完需要明白这个结论。

• 协方差矩阵的最大特征值对应的特征向量的方向，就是数据分布方差最大的方向。

基础知识

1：向量投影和内积

向量$A$在单位向量$B$上的投影可以理解为计算下图中绿色线段的长度。即$A\cdot B=\left|A\right|\cdot \left|B\right|\cdot cos(\alpha )$。

2：基变换

二维空间：$(0,1)$和$(1,0)$叫做一组基。

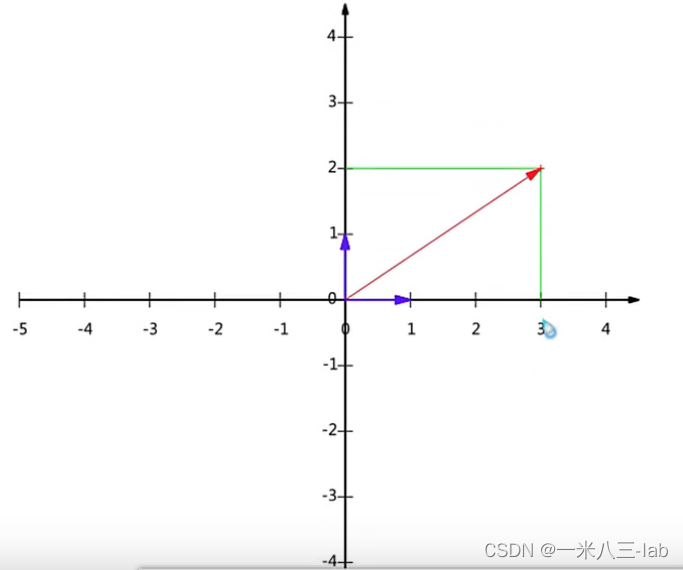
现在更换了一组基，以$(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})$和$(-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})$为一组新的基。所以点$\left[3,2\right]$在新的基坐标的表示下为：$\left[x^{{}^{\prime }},y^{{}^{\prime }}\right]=\left[3,2\right]\left[\begin{array}{cc}\frac{1}{\sqrt{2}}& -\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}& \frac{1}{\sqrt{2}}\end{array}\right]=\left[\frac{5}{\sqrt{2}},\frac{-1}{\sqrt{2}}\right]$。

通过新的基坐标表示，要想做到降维，那么就需要使得，原始坐标在新的基坐标表示下，至少有一个方向的投影很短，如下图所示，也就是说，之前需要用两个基坐标才能表示向量$A$，现在找到的基坐标，只要一个轴就能表示该向量$A$。

扩展到高维空间中公式表示就是：$Z_{m\times k}=X_{m\times n}\cdot W_{n\times k}$。其中$m$表示样本个数，$n$表示映射之前的特征维数，$k$表示映射后的特征维数。

PCA的原理

介绍

原始的数据集中，有很多特征可能是有一定关联的，例如对于人而言，有体重，身高等特征。很明显，身高和体重这两个特征是有一定的关联性的，身高越高，一般情况下，这个人体重就会越重。

所以可以考虑通过PCA的方法，将身高和体重变换到一个特征F中，这一个特征F就能尽可能多的表示原始的身高和体重两个特征，同时损失的信息非常少。

如果只是直接的扔掉身高或者体重某一个维度特征，这对数据集中单个人的特征而言，丢失的信息十分严重，所以通过PCA的方法，就可以使得特征信息损失尽量少的前提下，又达到降低维度的目的。

目标

将样本集$X_{m\times n}$，通过基变化矩阵$W_{n\times k}$，映射到新的$k$维特征子空间$Z_{m\times k}$中去，并且使得降维后的数据，在特征子空间$Z_{m\times k}$中坐标轴上的分布尽可能分散。

因为越分散，保留的信息就越多。（上面的图片二维降为一维已经很清晰了）

再说如果不分散，极端情况下都映射到一个点上，所有数据都一样，那就没意义了。数据的分散程度，我们使用方差来衡量，方差越大，数据越分散。

所以我们的目标，就是每次都要找，数据映射到该向量上的时候，保持方差最大，按照这个思路继续往下走。

步骤

假设我们要将数据投影到$k$个坐标轴上，则新的基需要含有$k$个向量，步骤如下:

• 将数据中心化，使得每个维度的均值为0。（不要问为什么，可以理解为，做了这步，后面算协方差的时候，均值就为0了，方便算协方差—我强行解释的）。
• 寻找一个单位向量$w_1$(坐标轴)，使得数据在该向量上的投影方差最大。$w_1$称为第一主成分。
• 寻找第二个单位向量$w_2$，使得$w_2$，与之前找到的向量$w_1$正交，并且在该向量上的投影方差次大(仅次于在$w_1$上的投影方差) 。$w_2$称为第二主成分。
• 按照如上的方式，依次寻找$w_3$, $w_4$, $\cdots$, $w_k$ 。$w_k$称为第$k$主成分。样本数据在$w_k$上的投影方差第$k$大。
• 将找到的所有$k$个单位向量$w_1,w_2,\cdots ,w_k$构成一个基，该基就是新的坐标系。
  我们将样本数据投影到该基上，就完成了正交变换。

具体步骤

第一步：数据去中心化。
将数据移到坐标轴中心，保持相对位置不变。（这一步在点云处理中，就是将坐标中心移到质心）。
第二步：计算投影方差。

• 定义$m$为样本数量，$n$为映射前的特征维度数，$k$为映射后的特征维度数量。

• $x^i=[x_1^i,x_2^i{]}^T$为样本集合中的第$i$组数据，$x_j^i$表示$x_i$的第$j$维度的特征。

• $u=[u_1^i,u_2^i{]}^T$为投影向量，$u^{T}u=1$。

• 向量$x^i$在向量$u$下的投影计算为：$d_i=\left|x_i\right|\cdot \left|u\right|\cdot cos(\alpha )=(x^i{)}^{T}u$
  
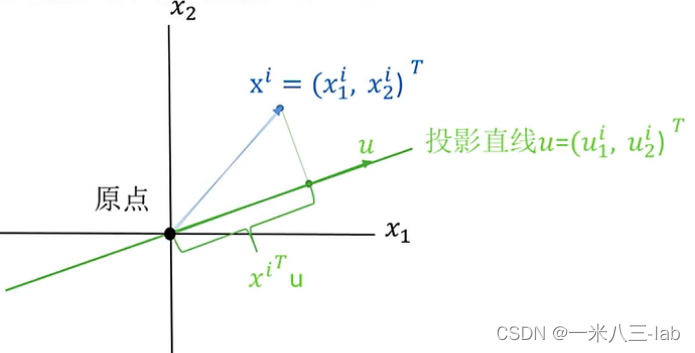
  所以，计算所有的数据$X_{m\times n}$（$m$个数据，一个数据维度为$n$维，这里很明显，$n$为2，设置了两个维度）投影到向量$u$的方差计算公式（自己百度一下方差公式）为：(这个公式结合后面的解释慢慢看，不难，很清晰，这步跳了后面更看不懂)。
  
  解释:（结合下面的解释，认真看，绝对能看懂，看不懂这个公式，点赞，收藏，然后退出该博客，去看这个视频吧：PCA算法原理剖析）

• 由于前面做了去中心化，所以$\bar{d}=0$；后面计算协方差的时候，涉及到的均值也是0。

• $<u,u>=u^T\cdot u=u^2$。所以$((x^i{)}^{T}u{)}^2=((x^i{)}^{T}u{)}^T\cdot ((x^i{)}^{T}u)$。

• $x^i$是一个列向量，算法原理第二步中对$x^i$进行了定义，所以$x^i\cdot (x^i{)}^T$是一个方阵。

• $u$是新的基坐标，它是和$x$无关的，所以在计算$S^2$的时候，可以提到前面去。

• 协方差计算公式为：

PCA算法目的

在高维数据中，找到高维数据中最大方差的方向，然后将其投影到维度更小的空间中。所以我们的目标函数就是$\{\begin{array}{c}max:S^2=u^{T}Cu\\ s.t:u\cdot u^T=1\end{array}$。找到$S^2$的最大值。

求目标函数最值

使用拉格朗日乘数法求解最值：$L(u,\lambda )=u^{T}Cu+\lambda (1-u^{T}u)$。不要忘记我们的变量是$u$。求解最值计算过程如下。

$\begin{array}{c}L(u,\lambda )=u^{T}Cu+\lambda (1-u^{T}u)\end{array}$

令$\begin{array}{c}\frac{\partial L}{\partial u}=2Cu-2\lambda u=0\\ Cu=\lambda u\end{array}$

所以目标函数改为如下：
$\{\begin{array}{c}max:S^2=u^{T}Cu=u^T\lambda u=\lambda u^{T}u=\lambda \\ s.t:u\cdot u^T=1\end{array}$

所以有以下两个结论。

• 我们的目标函数要求的，就是矩阵$C$最大的那个特征值。
• 向量$u$，由公式$Cu=\lambda u$可以知道，$\lambda$是矩阵$C$的特征值，$u$就是矩阵$C$的特征向量**
  （吐槽一下，真的是难懂）**

所以现在懂了为什么博客开始说的，协方差矩阵最大特征值对应的特征向量$v_1$，其方向为数据分布方差最大的方向了吧。

从上面推导我们已经知道了，要想让计算所有的数据$X_{m\times n}$在一个向量$u$上投影的方差最大，这里向量$u$就是协方差矩阵的最大特征值对应的那个特征向量，而且最大的方差，其值就为协方差矩阵的最大特征值。

同时协方差矩阵是实对称矩阵，其不同特征值对应的特征向量是正交的（性质记住），推给你们看。

求解第二个方差最大的向量

我们求到了第一大特征值对应的特征向量$u$，那么我们就需要将所有的数据$X$投影到特征向量$u$上面去，投影完以后，得到数据$X^{\ast }$以后，再在数据$X^{\ast }$基础之上，去找数据$X^{\ast }$对应的协方差矩阵，特征值最大的特征向量$w$。

原始数据$X$的协方差矩阵第二大特征值对应的特征向量$v_2$，其实就是这里数据$X^{\ast }$对应的协方差矩阵，特征值最大的特征向量$w$。其方向就是与特征向量$v1$垂直方向上，数据方差最大的方向；也就是说

• 第一：特征向量$v2$要垂直于特征向量$v1$；
• 第二：特征向量$v2$要使得原始数据$X$的分布方差第二大，使得数据$X^{\ast }$的分布方差最大。

回到求解点云法向量的思考

求解点云法向量的思路是，首先对于点云中的每个扫描点$p$，搜索到与其最近邻的$K$个相邻点，然后计算这些点的局部平面$H$，用该局部领域$H$来拟合这些邻域点的平面。然后法向量就是垂直于该平面的向量。

所以，局部平面$H$，先投影到特征向量$v1$上面去，使得方差最大；然后再投影到特征向量$v2$上面去，使得方差第二大，然后投影到第三个特征向量$v3$上面去的时候，特征向量$v3$就是该平面的法向量。（所以看到这里，应该多少懂了一开始的结论吧）

数据降维

现在就很简单了，求协方差矩阵的特征值和特征向量计算公式为$\left|\lambda E-C\right|x=0$，这里的$\lambda$估计不唯一，那么就会有多个特征向量，那么最终需要降到多少维，那么就使用多少个特征向量就行了。

然后我们选择前$k$个最大的特征值对应的特征向量，组成变换矩阵$W_{n\times k}$就可以了。即$W_{n\times k}=[u_1,u_2,\cdots ,u_k]$。

最后进行数据降维：$Z_{m\times k}=X_{m\times n}{W}_{n\times k}$。

PCA算法流程总结

1. 数据集$X_{m\times n}$去中心化。
2. 求数据集$X$的协方差矩阵$C$
3. 计算协方差矩阵$C$的特征值和特征向量
4. 选择前$k$个特征值对应的特征向量，组成转换矩阵$W_{n\times k}$
5. 最后进行数据降维：$Z_{m\times k}=X_{m\times n}{W}_{n\times k}$

继续吐槽

真难懂，好难搞，现在PCA和求解点云法向量已经讲完了，看到这里都不点赞，那就继续往下看吧，能坚持到这里的，基础应该是有一丝丝的。

下面的问题是，协方差矩阵的特征值怎么求呢，讲了半天，我还不知道怎么求协方差矩阵对应的特征值以及特征值对应的特征向量，所以下面就要用SVD算法。

SVD算法

使用SVD算法，用来求解协方差矩阵的特征值。

基础知识

开始之前，需要继续补充一些基础知识，不然会看不懂。

1：矩阵特征值和特性向量的关系

• 矩阵$A1：\left[\begin{array}{cc}3& 0\\ 0& 3\end{array}\right]$对向量$B：\left[\begin{array}{cc}1& 1\end{array}\right]$左乘的意义在于，将向量$B$进行缩放。计算公式如下$\left[\begin{array}{cc}3& 0\\ 0& 3\end{array}\right]\cdot \left[\begin{array}{c}1\\ 1\end{array}\right]=\left[\begin{array}{cc}3& 3\end{array}\right]$。
• 矩阵$A2：\left[\begin{array}{cc}3& 1\\ 0& 1\end{array}\right]$对向量$B：\left[\begin{array}{cc}1& 1\end{array}\right]$左乘的意义在于，将向量$B$进行缩放。计算公式如下$\left[\begin{array}{cc}3& 1\\ 0& 3\end{array}\right]\cdot \left[\begin{array}{c}1\\ 1\end{array}\right]=\left[\begin{array}{cc}4& 3\end{array}\right]$。

所以矩阵左乘一个列向量，其作用非常明显，就是旋转+缩放。
那么对于特征向量和特征值的关系是什么呢？首先求一个矩阵的特征向量和特征值满足如下关系。$Ax=\lambda x$，它的几何意义表示，一个矩阵$A$左乘一个列向量$x$，其结果等于该列向量$x$缩放$\lambda$倍。所以这个满足这种情况的列向量$x$表示矩阵$A$的特征向量，缩放倍数$\lambda$表示特征值。

特征值分解

并不是所有的方阵都可以进行特征值分解，只有可对角化的方阵才可以。那么问题来了，什么样的方阵可以对角化？
答案就是：$n\ast n$阶矩阵$A$可对角化的充分必要条件是矩阵$A$有$n$个线性无关的特征向量。言外之意就是

• 矩阵$A$的行列式$\left|\begin{array}{c}A\end{array}\right|\ne 0$；
• 对矩阵$A$进行行列式化简，不会出现全为$0$的一行元素；
• 方程$Ax=b$，一定存在唯一解，因为有$n$个方程，$n$个变量，所以可以确定唯一解。（线性代数知识）

---

特征值和特征向量的定义如下:

$Ax=\lambda x$；

其中$A$是一个$n\times n$的矩阵，$x$是一个$n$维向量，则我们说$\lambda$是矩阵$A$的一个特征值，而$x$是矩阵$A$的特征值$\lambda$所对应的特征向量。

求出特征值和特征向量以后，我们就可以将矩阵$A$进行特征分解。

如果我们求出了矩阵$A$的$n$个特征值，${\lambda }_1\le {\lambda }_2\le \cdots \le {\lambda }_n$，以及这$n$个特征值所对应的特征向量，$W=\left(\begin{array}{cccc}{w}_1& w_2& \cdots & w_n\end{array}\right)$。

那么矩阵$A$就可以用下式的特征分解表示:$A=W\sum W^{-1}$。

SVD奇异值分解

奇异值分解可以用来分解任意形状的矩阵，不一定非要是方阵。（我们求取点云法向量的时候，用的是协方差矩阵，协方差矩阵是一个实对称矩阵，SVD算法就更能用）

定义矩阵A的SVD为： $A=U\sum V^T$。

其中$A$矩阵的大小为$m\times n$；$U$是正交矩阵，矩阵的大小为$m\times m$；$\sum$是对角矩阵，其大小为$m\times n$；$V$是正交矩阵，矩阵的大小为$n\times n$。矩阵$U$和$V$都是酉矩阵，满足关系$U^{T}U=I,V^{T}V=I$。

如何计算矩阵$U$和$V$呢？

• $U$是的特征向量$A{A}^T$张成的一个矩阵;
• $V$是的特征向量$A^{T}A$张成的一个矩阵;
• $\sum$是$A{A}^T$或者$A^{T}A$特征值的平方根。
  下面给出证明：
  
  结合实际情况，给一个例子。
  
  这个例子，我们给它实际意义，矩阵$A$的第一列表示$x$坐标，矩阵$A$的第二列表示$y$坐标，那么我们通过$A^{T}A$可以计算得到矩阵$A$的协方差矩阵。

那么$A^{T}A$计算得到的特征向量，就是协方差对应的特征向量，也就是这里的$V$向量，这下懂了吧，代码里面的这几句。就是通过$SVD$分解计算得到$V$矩阵，第三个特征向量就是该平面的法向量。

cov = np.matmul(X, X.T) / (len(indN) - 1)
_, _, Vt = np.linalg.svd(cov)
normal = Vt[2, :]

结束语

全文内容有很多抄袭其他博客的地方，至少抄袭了十几个博客的内容，还有视频（不废话，写自己博客的时候，肯定要看别人的博客，自己又懒的画图，肯定要抄袭），但是里面的分析，肯定还是要按照自己的理解，参考就不放了（不是我不想放，是因为找不到了），就这么说吧。

果然比魔法还神奇的，还是数学。