读书笔记 | 自动驾驶中的雷达信号处理（第3章 雷达系统信号处理）

本文编辑：调皮哥的小助理

3.1介绍

本章主要介绍雷达接收信号处理的重点理论，主要对傅里叶变换及其在雷达信号处理中的应用，即本文主要是介绍数字信号处理中的相关内容在雷达信号处理中的应用，比如傅里叶变换、采样定理、加窗技术等等。

雷达信号处理的基础是数字信号处理，二者是承上启下，密不可分的关系，想要学好雷达信号处理，数字信号处理必然要十分熟悉。

3.1.1 傅里叶变换的定义

傅里叶变换的目的是将时域信号变换为频域信号。对于周期信号，信号的压缩表示成为可能。这意味着一系列时域信号可以用一个数字表示，即信号的频率，传输信号压缩是这一概念的一个流行应用。

有许多好的书籍和在线资料提供了关于傅里叶变换及其数学解释的不同层次的细节，这种分析超出了本章的范围，但我们的目的是给出必要的背景知识，因为傅里叶变换是雷达信号处理中使用的基本工具。

信号x(t)的傅里叶变换(FT)定义为：
$$X(\omega )={\int }_{-\infty }^{\infty }x(t){\mathrm{e}}^{-j\omega t}\mathrm{d}t,\omega \in (-\infty ,\infty )$$（3.1）
或
$$X(f)={\int }_{-\infty }^{\infty }x(t){\mathrm{e}}^{-j2\pi ft}\mathrm{d}t,f\in (-\infty ,\infty )$$（3.2）

傅里叶反变换(IFT)表示为：

$x(\mathrm{t})=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }x(t){\mathrm{e}}^{j\omega t}\mathrm{d}\omega$(3.3)
或
$x(t)=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }x(t){\mathrm{e}}^{j2\pi ft}\mathrm{d}f$(3.4)

上述定义提供了信号从时域到频域转换所需的基本关系，反之亦然。

3.1.2傅里叶变换的性质

本节概述了一些常用的傅里叶变换性质，并在适当的情况下，给出了该实用程序的一些简短注释：

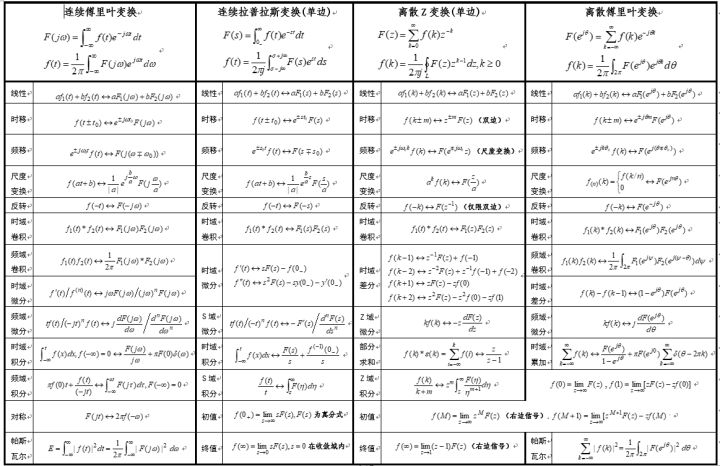
(图1 傅里叶变换性质)

注：上面这幅图是截图的，可能看不清楚，高清word图放在了公号（调皮连续波）后台，回复“信号与系统”即可下载。

3.1.3傅里叶级数

傅里叶级数是将一个周期信号分解成正弦函数的和。在数学上，分解可以这样进行

$s_N(t)=\frac{A_0}{2}+{\sum }_{n=1}^N{A}_n\sin \left(\frac{2\pi nt}{T}+{\phi }_N\right)$（3.5）

其中 $T$ 表示周期，N是正弦函数的数量，$A_n$ 是傅里叶系数，而其中 ${\phi }_N$ 是任意相位项，傅立叶级数展开的复数等价可以这样给出：

$s_N(t)=\frac{a_0}{2}+{\sum }_{n=1}^N{a}_n\cos \left(\frac{2\pi nt}{T}\right)+b_n\sin \left(\frac{2\pi nt}{T}\right)={\sum }_{n=-N}^N{c}_n{\mathrm{e}}^{-j\frac{2\pi nt}{T}}$（3.6）

傅里叶系数是：

$a_n=\frac{2}{T}{\int }_{t_0}^{t_0+T}s(t)\cos \left(\frac{2\pi nt}{T}\right)\mathrm{d}t$
$b_n=\frac{2}{T}{\int }_{t_0}^{t_0+T}s(t)\sin \left(\frac{2\pi nt}{T}\right)\mathrm{d}t$
$c_n=\frac{1}{T}{\int }_{t_0}^{t_0+T}s(t){\mathrm{e}}^{-j\frac{2\pi nt}{T}}\mathrm{d}t$ (3.7)

傅里叶系数可以被计算为：

$\begin{array}{rl}{A}_n& =\sqrt{a_n^2+b_n^2}\\ {\phi }_N& ={\tan }^{-1}\left(\frac{b_n}{a_n}\right)\end{array}$（3.8）

从上述等式可以看出，当 $N\to \infty$ 时，$s_N(t)$ 越逼近$\stackrel{ˉ}{}s(t)$， 傅里叶级数展开的一种用途是用于雷达波形生成，可提高对干扰的鲁棒性，如 [6] 和 [7] 中所述。

关于傅里叶级数的推导证明，推荐看这篇文章：傅里叶

3.1.4抽样定理（采样定理、取样定理）

数字信号处理是雷达处理中常用的一种方法，但前提必须是离散信号。采样定理定义了从采样数据恢复原始信号的条件。虽然存在有许多创新的采样方法，但是香农采样定理（奈奎斯特采样定理）仍然是标准。

奈奎斯特采样定理指出：如果 $x(t)$ 是带宽为B的带限信号，则可以从大于2B的采样率得到的样本恢复原始信号。在数学形式中，我们可以写为：

$x(t)={\sum }_{n=\infty }^{\infty }x(nT)g(t-nT),g(t)=\sin c\left({\omega }_{s}t\right)$（3.9）

其中，${\omega }_s=2\pi f_s$ 为弧度采样频率。关于上述采样定理的证明推导过程，可以自行查看相关资料。

BaronNashIstDD：浅谈推导Shannon采样定理

3.1.5离散傅里叶变换（DFT）

如3.1.1节所示，傅里叶变换由无限持续时间上的连续积分定义。在雷达处理等应用中，连续积分的计算是不可想象的，无限的持续时间要求是不可能实现的。为了克服这个限制，离散化傅里叶变换是必要的，这使得使用离散傅里叶变换计算样本数据的傅里叶变换成为可能。

根据定义，信号 $x(n)$ 的离散傅里叶变换(DFT)为:

$X(k)={\sum }_{n=0}^{N-1}x(n){\mathrm{e}}^{-j\frac{2\pi nk}{N}},k=0,1,\dots ,N-1$（3.10）

其中 $x(n)$ 是在 $n$ 时刻的采样信号， $k$ 是每秒弧度内的第 $k$ 个频率，$X(k)$ 是频率 $k$处的复值离散傅里叶变换， $X(k)$ 也可以认为是频率 $k$ 处的复谱。

我们可以类似地定义离散傅里叶反变换(IDFT)为：

$x(n)=\frac{1}{N}{\sum }_{k=0}^{N-1}X(k){\mathrm{e}}^{j\frac{2\pi nk}{N}},n=0,1,\dots ,N-1$（3.11）

DFT可以通过简单的乘法和加法运算来计算，因此可以很容易地在使用数字信号处理技术的大多数应用中使用。在实际应用中，采用FFT算法可以有效地计算DFT，使计算复杂度从 $N^2$ 阶降到最低 $N\log N$。在后面第3.2节中，离散傅里叶变换被可以用于距离-多普勒估计。

3.1.6功率谱估计

根据定义，功率谱是平稳过程的自相关序列的傅里叶变换，记住这个结论，非常重要。因此，对于一个信号 $x(t)$，其频谱估计 $S(f)$ 可以由下面公式表示：

$S(f)={\int }_{-\infty }^{\infty }{R}_{xx}(\tau ){\mathrm{e}}^{-j\omega t}\mathrm{d}\tau$（3.12）

在 $R_{xx}(\tau )$ 表示自相关函数。需要估计频谱的信号通常嵌入噪声中，因此高分辨率频谱估计技术是必不可少的。这一节的目的不是深入研究频谱估计的细节，而是给出一个非常简短的内容，因为它对汽车雷达处理很重要，在参考文献[13-15]中有深层次的讨论。关于“功率谱是平稳过程的自相关序列的傅里叶变换”这个结论的具体推导过程，可以看下面文章：

boy：关于自相关函数的两种定义与功率谱密度的两种定义

传统的谱估计方法仅依靠离散傅里叶变换(DFT)来获得观测数据序列的功率谱。其中流行的是周期图法和Blackman-Turkey法。然而，它们的主要缺点是使用短持续时间的数据序列无法分辨密集的频谱峰值。

这个缺点是研究高分辨率技术的主要目的，特别是自回归(AR)、滑动平均(ARMA)和特征分解技术。虽然这些高分辨率技术提供了更好的分辨率频谱估计，但只有在高信噪比(HSNRs)下，它们的性能才能保证优于传统方法。这可能是由于在低信噪比(LSNRs)下无法准确地将信号子空间从噪声子空间中分离出来。噪声的存在是AR参数估计中一个严重的非线性问题，更多详细信息请参见参考文献[12]。

虽然功率谱是自相关函数的定义项，但在实际应用中是用DFT估计的。FFT可以有效地计算DFT，因此得到了广泛的应用，在这种情况下，功率谱是FFT结果的幅值（重点）。

在雷达处理中，通常采用频谱估计来估计目标的距离和速度，而目标的角度是由高分辨率技术获得的，因为它通常是区分紧密相邻目标的理想算法。

关于谱估计的学习书籍，我这里推荐阅读《现代信号谱分析》：

电子版的在：干货 | 这些雷达书籍，你需要收藏~（终极大汇总）。

3.1.7 加窗技术

为了改进频谱估计结果需要加窗，因为 DFT 中使用的周期性假设要求估计的频率是频谱分辨率的整数倍，但这无法保证。结果是频谱不连续，进而导致能量扩散到多个频率区间，表现为旁瓣，这个问题可以通过使用窗函数来改善。

窗函数从零附近或零开始，然后在采样数据序列的中心增加到最大值，然后再次减小 。从卷积原理来看，加窗具有平滑信号频率响应的作用，与没有加窗的频谱相比旁瓣的幅度会降低。然而，加窗也会导致主瓣变宽，因此我们需要权衡利弊，并不是所有技术都只有好处没有坏处。

窗函数已经使用了很长时间，下面我们给出汽车雷达信号处理中常用的一些窗函数。

3.1.7.1矩形窗

窗函数由以下表达式定义：

$w(n)=1$（3.13）

窗口的作用是将数据序列乘以一个单位振幅（幅值为1）的矩形函数，因此相当于只使用观测序列。

3.1.7.2 帕森窗

窗口函数是由以下表达式定义的 B 样条函数:

$w(n)=\{\begin{array}{ll}1-6{\left(\frac{2n}{N}\right)}^2\left(1-\frac{2|n|}{N}\right)& 0\le |n|\le \frac{N}{4}\\ 2{\left(1-\frac{2|n|}{N}\right)}^3,& \frac{N}{4}<|n|\le \frac{N}{2}\end{array}$（3.14）

3.1.7.3 巴特莱特（Bartlett）窗（三角窗）

窗函数由以下表达式定义：

$w(n)=1-\left|\frac{n-\frac{N-1}{2}}{L/2}\right|$（3.15）

或
$w(n)=\{\begin{array}{ll}\left(\frac{2n}{N}\right),& 0\le n\le \frac{N}{2}\\ {\left(2-\frac{2n}{N}\right)}^1,& \frac{N}{2}<|n|\le N\end{array}$（3.16）

3.1.7.4 Welch窗（抛物线窗）

窗函数由以下表达式定义：

$w(n)=1-{\left(\frac{n-\frac{N-1}{2}}{\frac{N-1}{2}}\right)}^2$（3.17）

3.1.7.5 汉宁窗（Hanning，海宁窗）

汉窗是汽车雷达信号处理中常用的窗口之一，窗函数由下面的表达式定义：

$w(n)=0.5(1-\cos \left(\frac{2\pi n}{N-1}\right)$（3.18）

3.1.7.6汉明窗（Hamming，海明窗、哈明窗，改进的升余弦窗）

窗函数由下面的表达式定义：

$w(n)=0.54-0.46\cos \left(\frac{2\pi n}{N-1}\right)$（3.19）

3.1.7.7 Blackman窗

窗函数由下面的表达式定义：

$$w(n)=a0-a1\cos \left(\frac{2\pi n}{N-1}\right)+a2\cos \left(\frac{4\pi n}{N-1}\right)$$（3.20）
其中, $a0=0.42,a1=0.5$, and $a2=0.08$.

3.1.7.8 Nuttall 窗

窗函数由下面的表达式定义：

$$w(n)=a0-a1\cos \left(\frac{2\pi n}{N-1}\right)+a2\cos \left(\frac{4\pi n}{N-1}\right)-a3\cos \left(\frac{6\pi n}{N-1}\right)$$(3.21)
其中, $a0=0.355768,a1=0.487396,a2=0.144232$, and $a3=0.012604$ 。

3.1.7.9 Blackman–Nuttall 窗

窗函数由下面的表达式定义：

$$w(n)=a0-a1\cos \left(\frac{2\pi n}{N-1}\right)+a2\cos \left(\frac{4\pi n}{N-1}\right)-a3\cos \left(\frac{6\pi n}{N-1}\right)$$（3.22）
其中, $a0=0.3635819,a1=0.4891775,a2=0.1365995$, and $a3=0.0106411$ 。

3.1.7.10 Blackman–Harris窗

窗函数由下面的表达式定义：

$$w(n)=a0-a1\cos \left(\frac{2\pi n}{N-1}\right)+a2\cos \left(\frac{4\pi n}{N-1}\right)-a3\cos \left(\frac{6\pi n}{N-1}\right)$$（3.23）
其中， $a0=0.35875,a1=0.48829,a2=0.14128$, and $a3=0.01168$ 。

3.1.7.11 Flat-Top窗

窗函数由下面的表达式定义：

$$w(n)=a0-a1\cos \left(\frac{2\pi n}{N-1}\right)+a2\cos \left(\frac{4\pi n}{N-1}\right)-a3\cos \left(\frac{6\pi n}{N-1}\right)+a4\cos \left(\frac{8\pi n}{N-1}\right)$$（3.24）
其中, $a0=1,a1=1.93,a2=1.29,a3=0.388$, and $a4=0.028$ 。

3.1.7.12 Turkey窗

$$w(n)=\{\begin{array}{ll}0.5+0.5\cos \left(\pi \left(\frac{2n}{a(N-1)}-1\right)\right),& 0\le n<\frac{a(N-1)}{2}\\ 1,& \frac{a(N-1)}{2}\le n\le (N-1)\left(1-\frac{a}{2}\right)\\ 0.5+0.5\cos \left(\pi \left(\frac{2n}{a(N-1)}-\frac{2}{a}+1\right)\right),& (N-1)\left(1-\frac{a}{2}\right)<n\le (N-1)\end{array}$$（3.25）
其中，设置 $a=0$ 将得到矩形窗口，而设置 $a=1$ 将得到Hanning窗口。

3.1.7.13 Kaiser窗

窗函数由下面的表达式定义：

$w(n)=\frac{I_0\left(\pi \alpha \sqrt{1-{\left(\frac{2n}{N-1}\right)}^2}\right)}{I_0(\pi \alpha )}$（3.26）

其中, $I_0$ 是第一类的零阶修正贝塞尔函数， 主瓣宽度和旁瓣电平之间的权衡由调谐参数 $\alpha$ 决定。

3.1.7.14 Dolph–Chebyshev窗

窗函数由下面的表达式定义：

$\begin{array}{rl}{W}_0(k)& =\frac{\cos \left(N{\cos }^{-1}\left(\beta \cos \left(\frac{\pi k}{N}\right)\right)\right)}{\cos h\left(N\cos h^{-1}(\beta )\right)}\\ \beta & =\cos h\left(\frac{1}{N}\cos h^{-1}\left(10^{\alpha }\right)\right)\\ \cos h^{-1}(x)& =\ln \left(x+\sqrt{x^2}-1.0\right)\\ w_0(n)& =\frac{1}{N}\sum _{k=0}^{N-1}{W}_0(k){\mathrm{e}}^{j2\pi kn/N},-\frac{N}{2}\le n\le \frac{N}{2}\end{array}$（3.27）

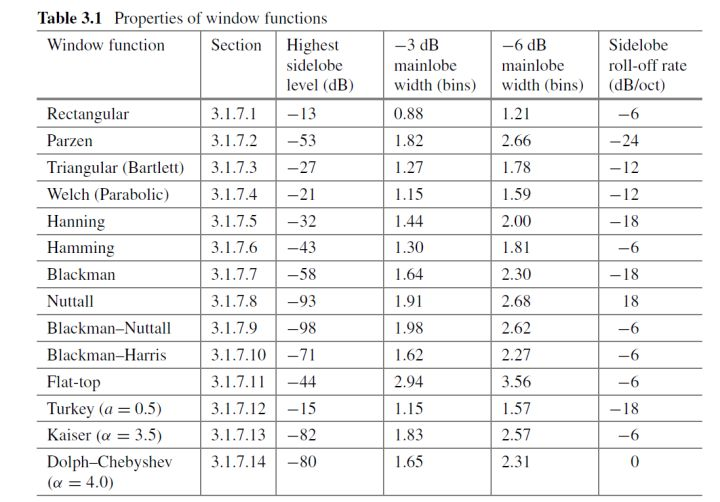
由式(3.27)可以看出，窗函数是通过逆DFT计算的，表3.1总结了上面描述的窗函数的属性：

3.2多维傅里叶变换(距离-多普勒估计的基础)

傅里叶变换理论可以推广到多维信号，对于雷达信号处理是二维(2D)和三维(3D)FFT，利用二维DFT可以计算距离-多普勒谱，实现雷达的基本功能。

此外，3D DFT可用于到达方向DOA估计。在本节中，我们将简要介绍二维DFT，因为它是理解高维傅里叶变换的关键。在大多数应用中，DFT都是通过快速傅里叶变换(FFT)算法实现的。

假设我们在大小为 $m\times n$ 的离散网格上定义了两个二维信号 $f(m,n)$ ，二维DFT结果由下面公式表示：

$\begin{array}{rl}F(k,l)& =\frac{1}{MN}\sum _{m=0}^{M-1}\sum _{n=0}^{N-1}f(m,n){\mathrm{e}}^{-j2\pi \left(\frac{k}{M}m+\frac{l}{N}n\right)},\\ k& =0,\dots ,M-1,l=0,\dots ,N-1\end{array}$（3.28）

逆DFT变换可以表示为：

$f(m,n)={\sum }_{k=0}^{M-1}{\sum }_{l=0}^{N-1}F(k,l){\mathrm{e}}^{j2\pi \left(\frac{k}{M}m+\frac{1}{N}n\right)},m=0,\dots ,M-1$
$n=0,\dots ,N-1$ (3.29)

下表总结了2D DFT的一些重要性质，比如周期性、共轭对称性、功率谱、平均值、卷积定理、等。

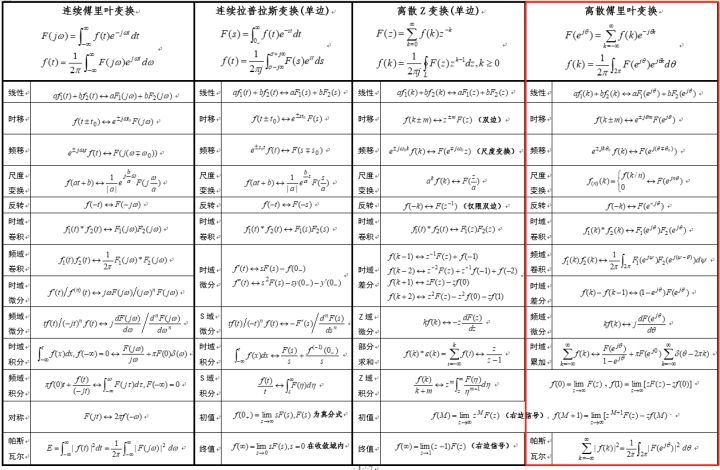
(图2 DFT性质)

注：上面这幅图是截图的，可能看不清楚，高清word图放在了公号（调皮连续波）后台，回复“信号与系统”即可下载。

3.3雷达信号噪声和杂波抑制

在实际应用中，雷达传感器接收到的信号总是包含噪声和杂波。噪声可以通过某种假设的统计分布来表征，而杂波则更难表征，因为它是表现得像目标一样的“不良障碍物”反射的结果。对于汽车雷达来说，杂波的来源包括雨、地面反射和路边建筑物。
事实上，雷达视场内的“非目标反射”可以被认为是杂波。杂波的干扰程度可以用信杂比来表征，信杂比取决于RCS、杂波反射率和杂波暴露程度等因素。 比可以纳入雷达方程，尽管不太容易，但由于杂波的动态性质，在某些情况下，当杂波信号为高斯分布时，最好采用杂波和噪声的组合作为接收信号的总干扰，这样就不用信噪比，而是用信杂加噪声比(SCNR)来代替信噪比。

因此，信噪比(SIR)可以表示为：

$\mathrm{SIR}=\frac{1}{\frac{1}{\mathrm{SCR}}+\frac{1}{\mathrm{SNR}}}$（3.30）

式中，SCR为信杂比。修正后的雷达方程就变成：

$R=\sqrt[4]{\frac{P_t{G}_t{A}_e{\sigma }_s}{k{T}_{0}B{F}_n\ast \mathrm{SIR}(4\pi {)}^{2}L}}$(3.31)

减少杂波影响的策略包括动目标显示(MTI)、脉冲多普勒处理和极化技术。采用窄波束宽度雷达天线和通过扩大带宽来提高距离分辨率对某些类型的杂波是有效的。这些附加措施的缺点是增加了雷达系统的复杂性、成本和尺寸。因此，为了将杂波抑制到理想的水平，最好是改进信号处理技术。