四元数的理解

一 四元数的可视化

一共三个虚维度来描述空间，实数则在第四个维度，垂直于全部三个虚数轴

四元数可以优雅的描述并计算三维旋转

“四维右手法则”

1.一维到二维（直线人小莱）

两个复数Z和W相乘，把z当成一个函数，对w施加某种旋转和拉伸 左边的数作为一种函数，去变换右边的数

原则上将，把所有二维旋转的集合映射到一维数轴上，那就是小莱的家了

球极投影

特殊方法，将圆映射到直线，或将球映射到平面，甚至将四维超球映射到三维空间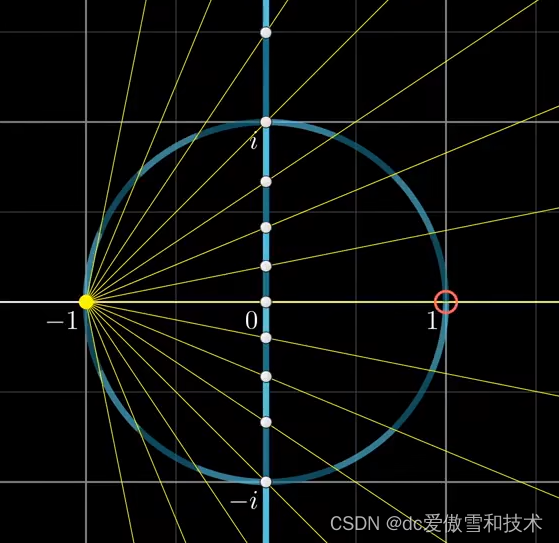 

 复数中距离原点长度为1的那些，即单位圆

 

2.二维到三维 （纸片人小菲）

球极投影会把单位球上的每一个点映射到i轴与j轴组成水平面上的唯一点

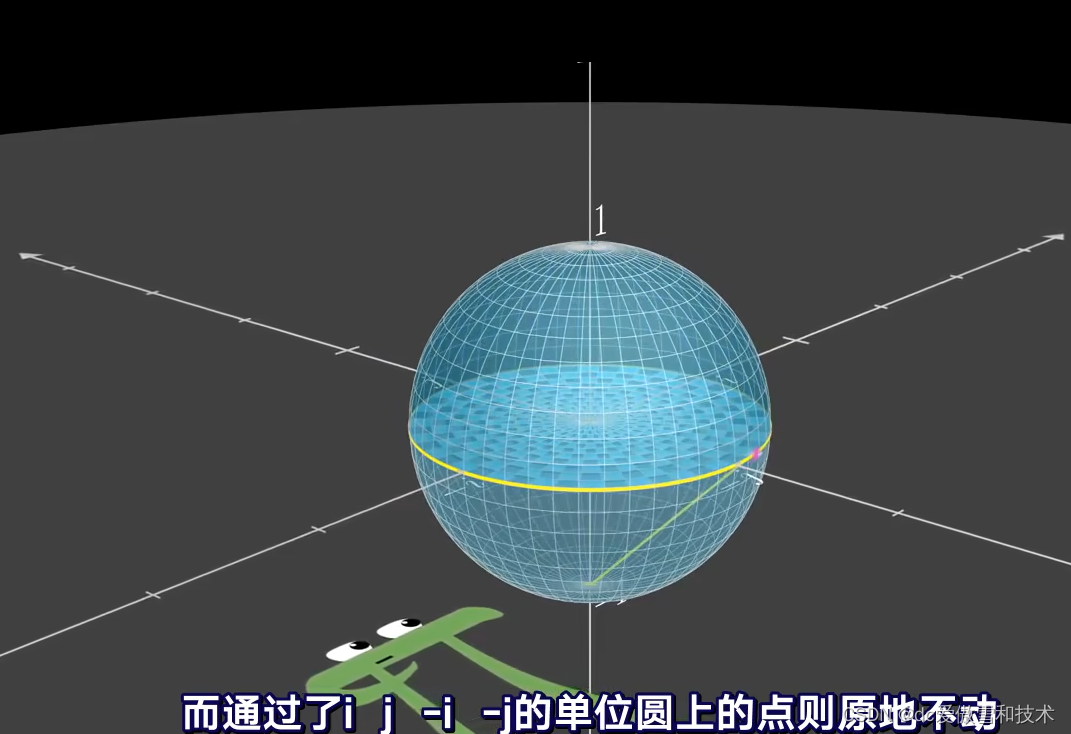
3.三维到四维 （我）

 三个虚数轴都和实数垂直，他们也都互相垂直 

 

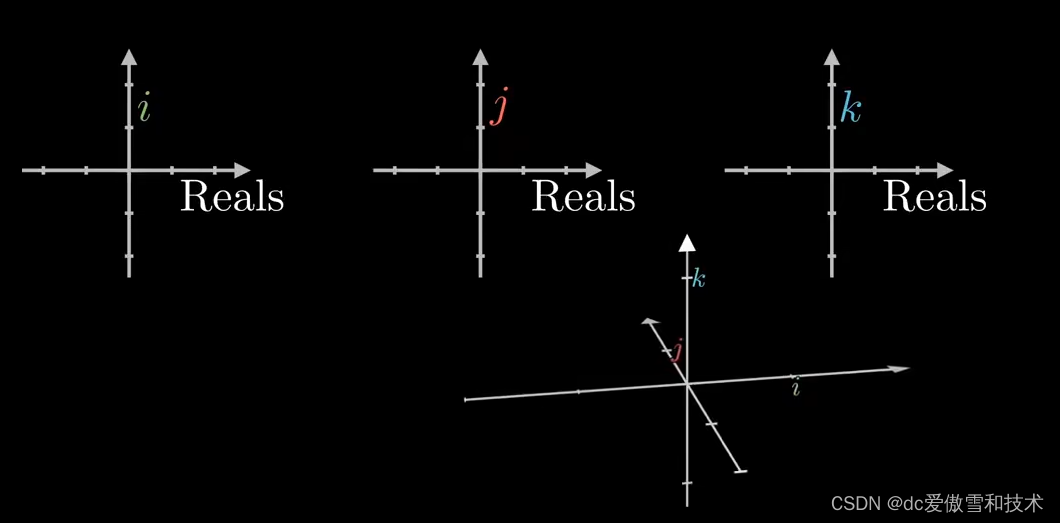
 把四维超球投影到三维空间 单位球代表着所有实部为0的四元数，所有点都代表一个单位四元数

实部为0到1的单位四元数，投影到了单位球的内部，靠近三维空间的1

在我们看不到的四维超球上，有一个单位三维球，通过1 i j -1 -i -j

两个圆互相垂直，不仅同心同半径而且完全不相交

取一个单位四元数并左乘另一个四元数，可以理解为两个独立的二维旋转 

从线性代数来理解，1 i j k是四维空间的基，所以知道了对他们的变换是什么就了解了对整个空间的变换

四元数-基本概念

1.为什么要用四元数

可能四元数的由来大家都看过很多遍。很久以前，一位老者坐在大桥边上，看着过往船只，突然灵光一闪，在桥边石碑上洋洋洒洒刻上几行大字，四元数诞生了！故事大家都爱听，那么为什么我们需要四元数？一种说法是解决向量乘法，我们知道向量之间乘法有内积和外积，但这两个运算均不完美，即不满足群的条件（当然四元数诞生的时候也还没有内积外积的说法）。那向量之间是否存在这样一个非常完美的乘法，于是三维空间无法解决的问题就映射到四维空间。这便是四元数诞生的契机。

那么问题又来了，既然四元数只是为了解决矩阵乘法，那为什么我们现在要用四元数进行旋转，甚至替代了欧拉角、轴角等形式？首先，四元数并不是生来为了解决三维旋转，而是它的性质非常有利于表达旋转信息（后面会详述），所以了解四元数的性质要先于了解四元数在旋转中的应用。至于四元数替代欧拉角等形式，就需要牵扯到一些别的知识点，我先罗列一下四元数相比其他形式的优点：

解决万向节死锁（Gimbal Lock）问题 仅需存储4个浮点数，相比矩阵更加轻量 四元数无论是求逆、串联等操作，相比矩阵更加高效

所以综合考虑，现在主流游戏或动画引擎都会以缩放向量+旋转四元数+平移向量的形式进行存储角色的运动数据。

2.四元数的提出

平庸的教程会直接提出四元数的定义、运算规则等等，然后读者不知所云。相反，较为系统的教程一般会从复数（Complex Number）进行引导，逐步提出四元数的定义，这样会让读者更容易理解，在脑中也更好形成画面。那复数与四元数之间的关系、以及如何从复数这样一个概念扩展到四元数是我们需要理清的一个思路。

先说几个概念。

空间中的子空间：一般而言，空间（维度>2）都存在更低维的子空间，比如二维空间中一维子空间，也就是直线；三维空间中的一维子空间和二维子空间，也就是直线和面。当超过三维的概念我们就很难去想象是什么样子，但四维空间一定会存在三维子空间或二维子空间。我们这里会加一个前缀超（hyper）来形容这些空间，比如高维空间中的平面我们称为超平面。

空间和子空间的映射：我们将二维空间表示为(x,y)，当y=0时，其实可以看成是一维的，只不过它表示成(x,0)这种形式。推到四维，(w,x,y,z)，当w=0时，(0,x,y,z)就是一个三维子空间，这也是为什么我们可以用单位四元数对三维向量进行操作，其实我们是将三维向量映射到四维的三维子空间（w=0，这种形式也成纯四元数），然后对其进行旋转，最终得到的向量结果依然是这个三维子空间中的，因而可以映射回三维空间。

四元数在处理三维空间中的旋转时的确是将三维向量嵌入到四维空间中进行操作。这里有几个关键点需要注意：

    纯四元数：在四元数中，当 w=0w=0 时，四元数 (0,x,y,z)(0,x,y,z) 被视为纯四元数。这种纯四元数可以用来表示三维空间中的向量。

    向量的四元数表示：三维向量 (x,y,z)(x,y,z) 可以表示为纯四元数 (0,x,y,z)(0,x,y,z)。这样，三维向量就被映射到了四维空间中的一个特定三维子空间。

    旋转的表示和应用：四元数旋转是通过单位四元数来表示的。要对一个三维向量应用旋转，我们首先将向量转换为纯四元数，然后使用四元数的乘法将其与旋转四元数相乘。

    旋转操作可以表示为：
    v′=q⋅v⋅q−1v′=q⋅v⋅q−1

    其中，vv 是要旋转的向量（作为纯四元数），qq 是表示旋转的单位四元数，v′v′ 是旋转后的向量。

    结果仍在三维子空间中：当对纯四元数（三维向量）应用旋转时，结果（v′v′）仍然是一个纯四元数。这意味着尽管在四维空间中进行了操作，但结果仍然属于原始的三维子空间。这允许我们将旋转后的结果无缝地映射回三维空间。

这种方法的优势在于它避免了使用传统欧拉角表示旋转时可能遇到的问题，如万向节锁，同时提供了一种数学上更稳定和高效的方式来处理复杂的三维旋转。

广义球：这里的球是广义上的。我们在二维平面上，广义球其实指代circle，三维空间上就是我们认知上的球，称为two-sphere，而四维空间中广义球其实是一个超球（hyper-sphere），又称为three-sphere。单位向量其实就是广义球上面的点，而单位四元数也就是three-sphere上面的点。

您提到的“广义球”是一个重要的概念，它在不同维度的空间中有不同的表现形式。让我们逐步解释这个概念：

1. **广义球的定义**：在数学中，广义球指的是在任意维度空间中所有到固定点（中心）距离相等的点的集合。这个固定距离被称为广义球的半径。

2. **不同维度中的广义球**：
   - **二维空间（平面）**：在二维空间中，广义球就是一个圆（circle）。所有点到圆心的距离（半径）相等。
   - **三维空间**：在三维空间中，广义球就是我们通常意义上的球（sphere），通常称为“two-sphere”（因为它的表面是二维的）。所有点到球心的距离相等。
   - **四维空间**：在四维空间中，广义球被称为超球或“three-sphere”。它是一个四维空间中的对象，其表面是三维的。所有点到中心点的距离相等。

3. **单位向量和单位四元数**：
   - **单位向量**：在任何维度的空间中，单位向量是指长度（或范数）为1的向量。在二维和三维空间中，单位向量分别位于圆和球（广义球）的表面上。
   - **单位四元数**：在四元数的上下文中，单位四元数是指其范数（或长度）为1的四元数。由于四元数可以表示为四维空间中的点，单位四元数就相当于位于四维空间中的超球（three-sphere）的表面上的点。

4. **理解单位四元数和三维超球的关系**：
   - 由于单位四元数的范数是1，它们定义了一个在四维空间中的超球表面。
   - 每个单位四元数都可以表示为四维空间中超球表面上的一个点。
   - 这种表示对于理解和可视化四元数在三维旋转中的作用是非常有用的。旋转可以视为在这个超球表面上的一种移动。

总的来说，将广义球的概念应用到不同维度的空间中，可以帮助我们更好地理解和可视化在这些空间中的几何和代数结构，特别是在处理复杂的旋转和方向问题时。在四维空间中，单位四元数与三维超球的联系为我们提供了一种强大的工具来处理和理解三维空间中的旋转。

约束与特征向量：空间中的一点由x, y, z等参数来表示，一般来说参数的数量与维数相等，二维空间的点用{x, y}参数，四维空间的点用{x, y, z, w}参数。但是对于空间的点加以约束，则该会减少参数的数量，比如三维空间的点在某一单位球面上，原本三个参数{x, y, z}才能表达的点现在只需要两个参数{u, v}就可以表达。如果{u, v}是单位向量，也可以称{u, v}是{x, y, z}的特征向量。 您的描述涉及到几个重要的几何和代数概念：空间中点的表示、约束对参数数量的影响，以及特征向量的概念。让我们逐一解释这些概念。

空间中点的表示

• 不同维度空间中点的表示：在不同维度的空间中，点的表示依赖于该空间的维数。例如，在二维空间中，点用两个参数 ( (x, y) ) 表示；在三维空间中，点用三个参数 ( (x, y, z) ) 表示；在四维空间中，则用四个参数 ( (x, y, z, w) ) 来表示。

约束与参数数量

• 约束的影响：当对空间中的点加以某种几何约束时，所需的参数数量可能会减少。例如，如果我们考虑三维空间中位于单位球面上的点，这些点满足约束 ( x^2 + y^2 + z^2 = 1 )。由于这个约束，原本需要三个参数来独立表示的点现在可以通过两个参数（比如球面坐标 ( u, v )）来表示。

特征向量的概念

• 特征向量的定义：特征向量是线性代数中的一个概念，通常与线性变换和矩阵相关。一个向量 ( \mathbf{v} ) 是某矩阵 ( A ) 的特征向量，如果它满足 ( A\mathbf{v} = \lambda\mathbf{v} )，其中 ( \lambda ) 是一个标量，称为特征值。

• 特征向量与空间中的点：在您的描述中，将单位向量 ( (u, v) ) 称为三维空间中点 ( (x, y, z) ) 的“特征向量”可能与传统的特征向量概念不完全一致。在这里，( (u, v) ) 更像是一种参数化表示，它们描述了在某个约束（如单位球面）下空间中点的位置。

理解和应用

• 在讨论约束时，重要的是理解通过减少自由度（如从三维空间到单位球面）可以减少描述空间中点所需的参数数量。
• 特征向量通常用于描述线性变换下保持方向不变的向量，而在几何上，它们通常不用来描述空间中点的位置。在您的情境中，“特征向量”更像是对约束空间内点的一种参数化描述。

总结来说，当对空间中的点施加几何约束时，确实可以通过减少参数数量来描述这些点。这在几何建模、计算机图形学和许多工程应用中是一个常见的概念。然而，将这种约束下的参数称为“特征向量”可能与特征向量在传统线性代数中的定义有所不同。

上述概念给了大家一个思路，四元数这样一个东西并不是一蹴而就的，从空间来说，它与我们熟知的低维空间本质上是没有区别的，或者说是有很大共性的。四元数的很多特性都是从低维拓展而来的，更具体的说是从复数这一概念拓展的。

复数概念很简单，它其实就是为了满足数学家的强迫症，-1的平方根要有意义。看似很没有意义的复数，在实际中却用处非凡。我们首先看一下它的几何表达形式，令x为实部，y为虚部，则x+iy可以表示为下图。 

复数的提出将原本一维的数值范围直接加了一个维度，数据量的增幅可以说是巨大的。那我们从极坐标的角度去思考复数，x+i·y可以写成r·cosθ+i·r·sinθ，我们只考虑单位复数，|r|=1，也就得到cosθ+i·sinθ。说到这，就要提一个代数学中常用的公式——欧拉公式，基本上复数的所有运算推到都会用到这个公式。 

接下来我先不说复数的乘法，单位复数乘法可以达到一个二维旋转的效果，有兴趣的可以在这里画一画，推一推。我先介绍如何从复数推导出四元数，正如复数是有一个实部和一个虚部组成的，那我们将一个虚部换成三个虚部，即两两相交{i, j, k}。

其中n为三维的单位向量，i²=j²=k²=i·j·k=-1。这便是四元数的常规表达形式，不过单位四元数是有一大堆的约束的，并不是所有四维向量都是四元数。

 这里再开一个脑洞，可能大家听说四元数、八元数，但是存在三元数、五元数？其实从客观上说，三元数、四元数、n元数都是存在的（也就是复数存在无穷个等级），但并不是所有的数系都满足模运算。而且随着维度的提高，特性会逐步牺牲，相比复数运算，四元数牺牲了交换律；相比四元数运算，八元数牺牲了结合律。当然也还存在十六元数，不过十六元数的特性将更少，在数学中也就更加没有意义，所以目前就四元数的应用最为广泛。

3.如何理解四元数

现在我们总结一下已经得出的四元数特性：

让我们推广到四维，w²+x²+y²+z²=1中取x、y和z来表示超球。如下图所示，四维空间投影到三维超平面（w=0）可能是一个two-sphere。当投影点在整个two-sphere的边缘时，w一定为0，值得一提的是在这个空间内的四元数是一个纯四元数。当投影点落在two-sphere的内部时，也分为两种情况，w>0和w<0。但是我们可以发现这两种情况下对应的特征向量是一样的，所以我们将旋转矩阵向四元数转换时，是有两个对应值的，四元数的范围是2倍覆盖于3D旋转（2:1 mapping）。 

参考文章文章链接

四元数——基本概念 - 知乎

四元数的可视化_哔哩哔哩_bilibili