目录
📝论文下载地址
🔨代码下载地址
👨🎓论文作者
📦模型讲解
[背景介绍]
任意的定向目标检测任务主要用于遥感图像目标检测和场景文字目标检测。多方向目标检测的最新进展主要是由经典目标检测方法的修改,使用旋转的边界框或四边形来表示多方向目标。由于遥感图像的复杂性以及大量小的,杂乱的和旋转的目标,旋转检测模型的鲁棒性极为重要。
[模型解读]
下图是作者方法的总体架构,该方法是基于RetinaNet的一步目标检测方法,包括基于回归的预测分支和基于CSL的预测分支。从图中可以看出,基于CSL的方法对于学习对象的方向和比例信息更为准确。

[基于回归的旋转检测方法]
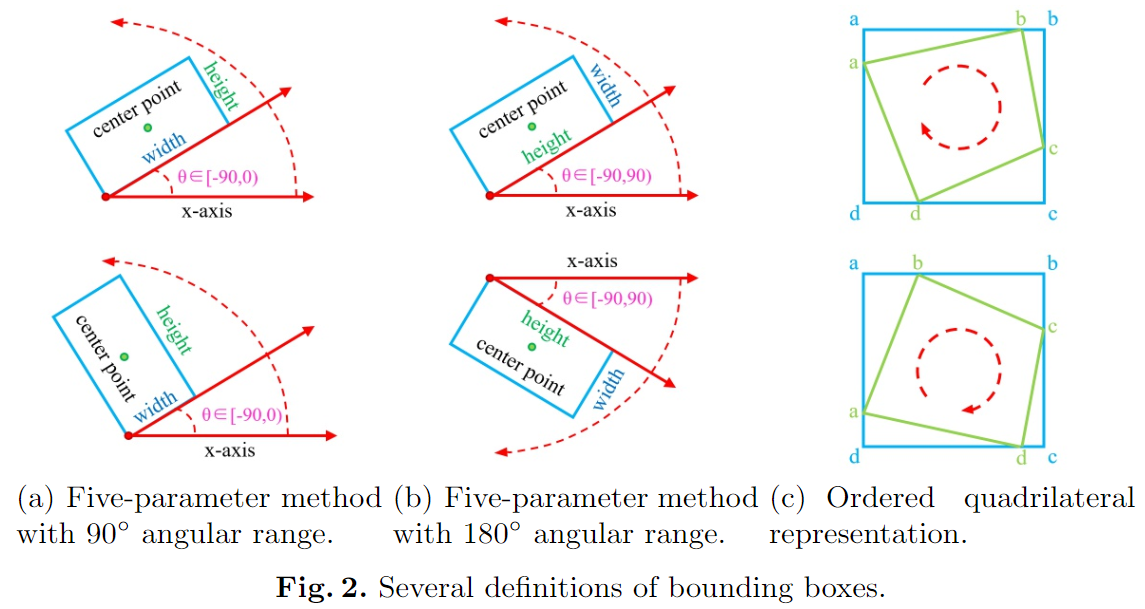
参数回归是当前旋转目标检测的一种常见方法,主要包括基于五参数回归的方法和基于八参数回归的方法。常用的基于五参数回归的方法通过添加额外的角度参数 θ \theta θ来实现面向任意方向的边界框检测。上图(a)显示了具有90°角度范围的矩形定义 ( x , y , w , h , θ ) (x,y,w,h,\theta) (x,y,w,h,θ), θ \theta θ表示相对于 x x x轴的锐角,与 x x x轴夹角的边为 w w w。上图(b)中所示的另一定义 ( x , y , h , w , θ ) (x,y,h,w,θ) (x,y,h,w,θ)区别开,其定义为180°角度范围,其 θ \theta θ由矩形的长边 h h h和 x x x轴的夹角。基于八参数回归的检测模型直接回归对象的四个点 ( x 1 , y 1 , x 2 , y 2 , x 3 , y 3 , x 4 , y 4 ) (x_1,y_1,x2,y_2,x_3,y_3,x_4,y_4) (x1,y1,x2,y2,x3,y3,x4,y4),因此预测是任意四边形。
[回归方法的边界问题]
在水平框检测模型中,参数化回归取得很好的性能,但是这些方法在任意定向框检测模型上会遇到边界不连续的问题。边界不连续性问题通常是由五参数方法中的角周期性和八参数方法中的点序引起的。边界不连续性问题通常会使模型在边界处的损失值突然增加。因此,这些检测方法在边界条件下常常不准确。作者根据回归方法的三种典型不同表示形式描述边界问题(前两个是五参数方法):
[opencv五参数表示法]
这种五参数表示法是opencv采用的表示方法,特点就是 θ \theta θ角度范围只有 [ − 90 , 0 ) [-90,0) [−90,0)度,但是框的 w / h w/h w/h会切换。由于角度的周期性(PoA)和边缘的交换性(EoE),这种情况的损失非常大,请参见图下中的示例说明。

[长边五参数表示法]
这种五参数表示法是常用的表示方法,特点就是 θ \theta θ角度范围有 [ − 90 , 90 ) [-90,90) [−90,90)度,框的 w / h w/h w/h不会切换,长边是 h h h,短边是 w w w。类似地,该方法还存在由边界处的PoA引起的损失急剧增加的问题。模型最终将选择将预选框顺时针旋转一个大角度,以获得最终的预测边界框。

[八参数表示法]
通过进一步的分析,由于四点的排序,八参数回归方法中仍然存在边界不连续性问题。考虑边界情况下八参数回归的情况,理想回归过程应为 { ( a → b ) , ( b → c ) , ( c → d ) , ( d → a ) } \{(a\rightarrow b),(b\rightarrow c),(c\rightarrow d),(d\rightarrow a)\} {(a→b),(b→c),(c→d),(d→a)},但实际回归过程应为蓝色预选框到绿色真实框是 { ( a → a ) , ( b → b ) , ( c → c ) , ( d → d ) } \{(a\rightarrow a),(b\rightarrow b),(c\rightarrow c),(d\rightarrow d)\} {(a→a),(b→b),(c→c),(d→d)}。实际上,这种情况也属于PoA。

基于以上分析,提出了一些解决这些问题的方法。例如,IoU平滑L1损失引入了IoU因子,而模块化旋转损失则增加了边界约束,从而消除了边界损失的突然增加并降低了模型学习的难度。在本文中,作者将从一个新的角度出发,将回归替换为分类,以实现更好,更强大的旋转检测。基于回归的一些经典的旋转检测模型进行了可视化比较,如下图(a)至(e)所示。基于CLS的方法没有边界问题,如图(i)所示。虚线为检测不好的结果。

[角度分类的圆形平滑标签]
[One-hot]
基于回归方法的边界问题的主要原因是预测超出了定义的范围。作者将角度预测作为分类问题,以更好地限制预测结果。一种简单的解决方案是将目标角度作为一个类别标签,并且类别的数量与角度范围有关。下图(a)显示了用于标准分类问题的one-hot编码的标签设置。

从回归到分类的转换可能会导致某些准确性误差。以180°角度范围的五参数方法为例,每个间隔的
ω
\omega
ω是一个类别。可以计算出最大精度误差
M
a
x
(
l
o
s
s
)
Max(loss)
Max(loss)和预期精度误差
E
(
l
o
s
s
)
E(loss)
E(loss):
M
a
x
(
los
s
)
=
ω
/
2
E
(
los
s
)
=
∫
a
b
x
∗
1
b
−
a
d
x
=
∫
0
ω
/
2
x
∗
1
ω
/
2
−
0
d
x
=
ω
4
\begin{aligned} M a x(\operatorname{los} s) &=\omega / 2 \\ E(\operatorname{los} s) &=\int_{a}^{b} x * \frac{1}{b-a} d x=\int_{0}^{\omega / 2} x * \frac{1}{\omega / 2-0} d x=\frac{\omega}{4} \end{aligned}
Max(loss)E(loss)=ω/2=∫abx∗b−a1dx=∫0ω/2x∗ω/2−01dx=4ω
根据以上公式,可以看出旋转检测的误差会很小。例如,当两个长宽比为1:9的矩形在角度相差0.25°和0.5°时,它们之间的IoU仅减少0.02和0.05。但是,One-hot标签对于旋转检测有两个缺点:
①当边界框使用基于90°回归的方法时,EoE问题仍然存在。此外,基于90°回归的方法具有两种不同的边界情况(垂直和水平),而基于180°回归的方法仅具有垂直边界情况。
②分类损失对于预测标签和地面真相标签之间的角度距离是不可知的。如上图所示,当真实角度为0°,分类器的预测结果分别为1°和-90°时,它们的分类损失相同。
[CSL]
因此,作者设计了一种圆形平滑标签(CSL),以通过分类获得更鲁棒的角度预测,而不会遇到包括EoE和PoA在内的边界条件。从下图可以清楚地看到,CSL包含具有周期性的圆形标签编码,并且分配的标签值是平滑的且具有一定的方差。

CSL的表达如下:
C
S
L
(
x
)
=
{
g
(
x
)
,
θ
−
r
<
x
<
θ
+
r
0
,
otherwise
C S L(x)=\left\{\begin{array}{cc}g(x), &\theta-r<x<\theta+r \\0, & \text { otherwise }\end{array}\right.
CSL(x)={g(x),0,θ−r<x<θ+r otherwise
其中,
g
(
x
)
g(x)
g(x)是一个窗口函数,是窗口函数的半径
θ
\theta
θ表示当前边界框的角度。需要理想的窗口函数
g
(
x
)
g(x)
g(x)拥有以下属性:
①周期性
g
(
x
)
=
g
(
x
+
k
T
)
,
k
∈
N
.
T
=
180
/
ω
g(x)= g(x + kT),k \in N.T= 180 /\omega
g(x)=g(x+kT),k∈N.T=180/ω表示将角度划分为类别数,默认值为180。
②对称性
0
≤
g
(
θ
+
ε
)
=
g
(
θ
−
ε
)
≤
1
,
∣
ε
∣
<
r
0 \leq g(\theta+\varepsilon)=g(\theta-\varepsilon) \leq 1,|\varepsilon|<r
0≤g(θ+ε)=g(θ−ε)≤1,∣ε∣<r,
θ
\theta
θ是对称中心。
③最大值
g
(
θ
)
=
1
g(\theta)=1
g(θ)=1
④单调性
0
≤
g
(
θ
±
ε
)
≤
g
(
θ
±
s
)
≤
1
,
∣
s
∣
<
∣
ε
∣
<
r
0 \leq g(\theta \pm \varepsilon) \leq g(\theta \pm s) \leq 1,|s|<|\varepsilon|<r
0≤g(θ±ε)≤g(θ±s)≤1,∣s∣<∣ε∣<r从中心点到两侧,函数呈现单调不递增的趋势。
作者提供了满足上述三个属性的四个窗函数:脉冲函数,矩形函数,三角形函数和高斯函数,如上图所示。标签值在边界处是连续的,并且不会由于CSL的周期性而造成精度误差。另外,当窗口函数是脉冲函数或窗口函数的半径很小时,One-hot等效于CSL。
[损失函数]
多任务管道包含基于回归的预测分支和基于CSL的预测分支。边界框的回归为:
t
x
=
(
x
−
x
a
)
/
w
a
,
t
y
=
(
y
−
y
a
)
/
h
a
t_{x}=\left(x-x_{a}\right) / w_{a}, t_{y}=\left(y-y_{a}\right) / h_{a}
tx=(x−xa)/wa,ty=(y−ya)/ha
t
w
=
log
(
w
/
w
a
)
,
t
h
=
log
(
h
/
h
a
)
t_{w}=\log \left(w / w_{a}\right), t_{h}=\log \left(h / h_{a}\right)
tw=log(w/wa),th=log(h/ha)
t
θ
=
(
θ
−
θ
a
)
⋅
π
/
180
(
o
n
l
y
f
o
r
r
e
g
r
e
s
s
i
o
n
b
r
a
n
c
h
)
t_{\theta}=\left(\theta-\theta_{a}\right) \cdot \pi / 180 \quad(only for regression branch)
tθ=(θ−θa)⋅π/180(onlyforregressionbranch)
t x ′ = ( x ′ − x a ) / w a , t y ′ = ( y ′ − y a ) / h a t_{x}^{\prime}=\left(x^{\prime}-x_{a}\right) / w_{a}, t_{y}^{\prime}=\left(y^{\prime}-y_{a}\right) / h_{a} tx′=(x′−xa)/wa,ty′=(y′−ya)/ha t w ′ = log ( w ′ / w a ) , t h ′ = log ( h ′ / h a ) t_{w}^{\prime}=\log \left(w^{\prime} / w_{a}\right), t_{h}^{\prime}=\log \left(h^{\prime} / h_{a}\right) tw′=log(w′/wa),th′=log(h′/ha) t θ ′ = ( θ ′ − θ a ) ⋅ π / 180 ( o n l y f o r r e g r e s s i o n b r a n c h ) t_{\theta}^{\prime}=\left(\theta^{\prime}-\theta_{a}\right) \cdot \pi / 180 \quad(only for regression branch) tθ′=(θ′−θa)⋅π/180(onlyforregressionbranch)
其中,
x
,
y
,
w
,
h
,
θ
x,y,w,h,\theta
x,y,w,h,θ分别表示框的中心坐标,宽度,高度和角度。变量
x
,
x
a
,
x
′
x,x_a,x^\prime
x,xa,x′分别是真实框,预选框和预测框。使用多任务损失,其定义如下:
L
=
λ
1
N
∑
n
=
1
N
o
b
j
n
⋅
∑
j
∈
{
x
,
y
,
w
,
h
,
θ
r
e
g
}
L
r
e
g
(
v
n
j
′
,
v
n
j
)
+
λ
2
N
∑
n
=
1
N
L
C
S
L
(
θ
n
′
,
θ
n
)
+
λ
3
N
∑
n
=
1
N
L
c
l
s
(
p
n
,
t
n
)
\begin{aligned} L=& \frac{\lambda_{1}}{N} \sum_{n=1}^{N} o b j_{n} \cdot \sum_{j \in\left\{x, y, w, h, \theta_{r e g}\right\}} L_{r e g}\left(v_{n j}^{\prime}, v_{n j}\right) \\ &+\frac{\lambda_{2}}{N} \sum_{n=1}^{N} L_{C S L}\left(\theta_{n}^{\prime}, \theta_{n}\right)+\frac{\lambda_{3}}{N} \sum_{n=1}^{N} L_{c l s}\left(p_{n}, t_{n}\right) \end{aligned}
L=Nλ1n=1∑Nobjn⋅j∈{x,y,w,h,θreg}∑Lreg(vnj′,vnj)+Nλ2n=1∑NLCSL(θn′,θn)+Nλ3n=1∑NLcls(pn,tn)
其中,
N
N
N表示锚点的数量,
o
b
j
n
obj_n
objn是二进制值(对于前景,也就是正样本,
o
b
j
n
=
1
obj_n = 1
objn=1;对于背景,
o
b
j
n
=
0
obj_n = 0
objn=0为负样本不回归)。
v
∗
j
′
v^\prime_{*j}
v∗j′表示预测出的偏移量,
v
∗
j
v_{*j}
v∗j表示预测的目标真值。
θ
n
,
θ
n
′
\theta_n ,\theta_n^\prime
θn,θn′表示真实的角度、预测的角度。
t
n
t_n
tn表示目标的类别标签,
p
n
p_n
pn是通过Sigmoid函数计算各种类别的概率分布。超参数
λ
1
=
1
,
λ
2
=
0.5
,
λ
3
=
1
\lambda_1=1,\lambda_2=0.5,\lambda_3=1
λ1=1,λ2=0.5,λ3=1。分类损失
L
c
l
s
是
F
o
c
a
l
L
o
s
s
L_{cls}是Focal Loss
Lcls是FocalLoss和
L
C
S
L
L_{CSL}
LCSL是Sigmoid交叉熵损失。回归损失
L
r
e
g
L_{reg}
Lreg是平滑的L1损失。
[结果分析]
[数据集]
作者使用的数据集是DOTA、ICADAR 2015、ICDAR 2017 MLT、HRSC2016。
[消融研究]
[窗函数]
DOTA数据集上四个窗口函数的比较。 5-mAP是指五个类别的平均平均精度。mAP表示所有15个类别的平均精度。 EoE表示边缘的交换性问题,表中的对勾表示该方法受到EoE的困扰。所有方法采用CSL所以都没有角度(PoA)问题的周期性。
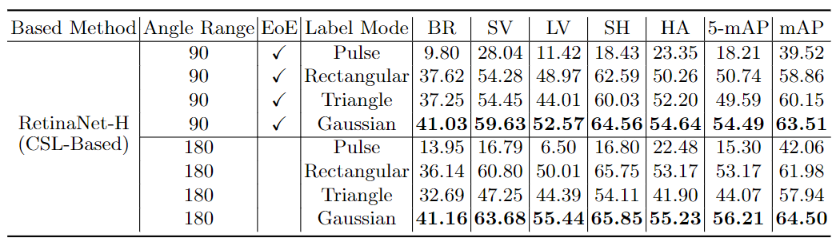
[窗函数半径]


上图中红色框是漏检情况,绿色是检测正确的框。
[CSL]
下表说明分类要比回归效果更好。
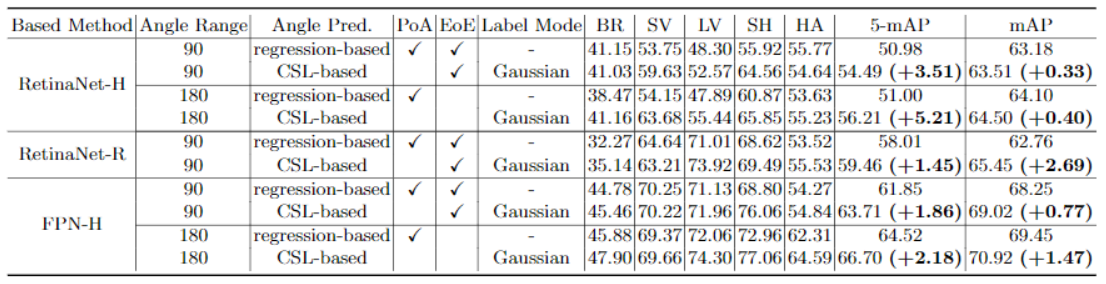









 本文介绍了一种基于分类的旋转检测方法,解决了传统回归方法在边界条件下的不连续性问题,提出了圆形平滑标签(CSL)策略,显著提高了检测精度。
本文介绍了一种基于分类的旋转检测方法,解决了传统回归方法在边界条件下的不连续性问题,提出了圆形平滑标签(CSL)策略,显著提高了检测精度。
















 4028
4028

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








