续上篇 揭秘大语言模型:从零到一的完整训练指南(一)——预训练-CSDN博客 已经介绍完预训练细节,本文将插播介绍一下MoE,即混合专家模型。由于该模型被目前大多主流大模型所追捧,因此不得不在开启后续训练介绍前,先带大家捋一遍MoE。
我们带着以下几个问题逐步展开:
1. 什么是MoE?
2. 它的结构是啥样的(组成部分)?它是怎么实现的(原理)?
3. 它是怎么用的?用在大模型的哪里?
一、关于MoE(什么是MoE)
至于说MoE的发展历程,这里就不废话了,因为我又不是MoE的创始人,跟大家扯历史我也是各种网上扒材料,没必要。我在网上找了张比较综合的图:

大家感兴趣可以看一下MoE盘古时期的论文:Adaptive Mixture of Local Experts。总的来说,朴素原理下的MoE并不是什么新奇玩意儿,只是当下有如是大佬不知道怎么开悟了,然后从尘封的百宝箱中将它拾起,弹去陈旧的灰,然后加工了一下,塞进了大模型,结果发现,效果duangduang的。这个诞生于1991年的古老创意,在30年后的大模型时代突然焕发新生,它让AI告别了"单核CPU硬扛"的笨重模式,转而进化成随时能召唤复仇者联盟的智能调度大师,当你惊叹大模型突然变聪明时,说不定就是它在暗地里悄悄摇来了几百个专家朋友。
那么怎么理解专家混合模型呢?所谓的专家混合模型,实际上就是一种具备门控功能的前馈神经网络,而所谓的门控,实际上就是一系列比较骚气的矩阵变换计算加上softmax计算一些得分权重,有点像注意力机制,有点像LSTM的门控,(我只是说有点像,勿杠),这些得分权重会给到每个专家,权重高的专家被选中处理token的概率最大,有时候会选top-k个专家进行融合。当然,目前的MoE还做了一些优化,负载均衡就是非常重要的一种优化,也是学习MoE的难点。
我们再通俗一点理解,想象一下火锅店的明档厨房:当你说"要微辣的牛肉锅",主厨立即调配卤味师傅调汤底、刀工师傅切雪花肥牛、酱料师傅调蘸碟。MoE的工作方式就像这样——每个"专家"都是细分领域的米其林大厨,而智能路由(门控)就是那个最懂食客的领班,瞬间组建最适合的料理天团。
有了大致的感性认识,我们当然接下来需要回归理性,结合一下实际代码更加深入的体会它的精髓啦。
二、MoE实现原理
先回答它的结构组成是怎样的。MoE整体上由两个关键部分组成:门控网络(或者路由,由一堆矩阵运算实现)和专家(本质上是前馈网络FFN)。
接下来我们一步步拆解MoE的实现(重点)。
1. 门控网络
门控网络之于整个MoE来说,有点像医院的导诊台,来了看病的潜在患者,有时候他们可能只能描述自己的症状特征,却不知道该找哪位专家看病,这个时候,导诊台就起到了特征识别和基本判断与分流的作用了,他们能根据潜在患者自述的特征,判断出他们应该挂哪种科室的号。那么门控网络就是需要判断输入序列的特征,以确定每个token该由哪个”专家“负责。
1.1 初始化定义
我们首先确定一下一共需要几个专家、真正执行专家操作时选top几个专家、门控网络的隐层维度等:
top_k = 2 #sparse moe,不是所有专家都选,而是选topk个专家
n_routed_experts = 4 #总专家数
scoring_func = 'softmax' #得分计算函数,用于计算专家的权重
alpha = 0.1 #辅助损失的系数
seq_aux = True #是否计算序列的辅助损失
norm_topk_prob = True #是否对topk概率归一化
gating_dim = 512 #门控隐层维度,等于hidden_size维度
weight = nn.Parameter(torch.empty((n_routed_experts, gating_dim))) #
print(weight)
print(weight.shape)
输出:
Parameter containing:
tensor([[1.4013e-45, 0.0000e+00, 2.6273e-10, ..., 4.5870e-41, 2.6278e-10,
0.0000e+00],
[9.8091e-45, 4.5870e-41, 2.6279e-10, ..., 4.5869e-41, 0.0000e+00,
0.0000e+00],
[0.0000e+00, 0.0000e+00, 5.6052e-45, ..., 0.0000e+00, 3.2230e-44,
0.0000e+00],
[2.6290e-10, 0.0000e+00, 1.5877e-42, ..., 0.0000e+00, 2.6172e-10,
0.0000e+00]], requires_grad=True)
torch.Size([4, 512])用kaiming初始化weight(也可以用其它的初始化方法),weight用于隐层hidden_size的专家空间映射:
init.kaiming_uniform_(weight, a=math.sqrt(5))
print(weight)
print(weight.shape)
输出:
Parameter containing:
tensor([[-0.0204, -0.0038, -0.0194, ..., -0.0198, -0.0076, 0.0132],
[ 0.0194, 0.0029, 0.0393, ..., 0.0342, -0.0414, -0.0274],
[-0.0154, -0.0400, 0.0019, ..., -0.0304, 0.0003, 0.0026],
[-0.0316, -0.0085, 0.0232, ..., 0.0390, -0.0162, -0.0422]],
requires_grad=True)
torch.Size([4, 512])完成上述初始化定义后,我们假设self-attention计算输出为 hidden_states,为了方便讲解,我们构造一个这样的张量:
hidden_states = torch.randn(32, 511, 512) # [batch, seq_len, dim]1.2 计算专家得分
所谓的专家计算,是针对每个token来说的,也就是说,每个token的语义计算都有专门的专家负责(一个或多个),那么为了方便计算,我们可以把batch-size和seq-len合并起来,即hidden_states的维度变为 [32*511, 512],接着我们就需要让每个token都映射在所有专家身上,可以这么理解,对于某个token,先让所有专家都看一遍,让每个专家心里都有个数,自己对该token的熟悉程度为多少,然后再具体将熟悉程度量化(计算专家得分 scores)。
bsz, seq_len, h = hidden_states.shape
hidden_states = hidden_states.view(-1, h)
hidden_states.shape
输出:torch.Size([16352, 512])
# 计算logits,即用线性变换函数将每个token向量映射到4个专家,并对logits进行softmax得分计算,算出4个专家对于同一个token的贡献度(专家得分)
logits = F.linear(hidden_states, weight, None)
print(hidden_states.shape, '——>', logits.shape)
输出:torch.Size([16352, 512]) ——> torch.Size([16352, 4])
# softmax归一化得分
scores = logits.softmax(dim=-1)
print(scores)
print(scores.shape)
输出:
tensor([[0.2948, 0.1252, 0.4110, 0.1689],
[0.2573, 0.2172, 0.3774, 0.1481],
[0.2643, 0.0792, 0.4702, 0.1863],
...,
[0.2254, 0.2044, 0.2058, 0.3643],
[0.4094, 0.2653, 0.1408, 0.1845],
[0.1826, 0.2848, 0.3826, 0.1499]], grad_fn=<SoftmaxBackward0>)
torch.Size([16352, 4])1.3 计算topK专家得分与相应索引位置
如果不想所有专家都选,而是选其中的对于某token最熟悉的topK个专家,那么我们就取每个token所选专家中得分topk的专家score,这里取top2,topk_weight是每个token前两名专家的得分矩阵,来源于scores,topk_idx为取到的前topk个专家的id,比如[2, 0]即为取第三个专家和第一个专家:
topk_weight, topk_idx = torch.topk(scores, k=top_k, dim=-1, sorted=False)
print(topk_weight, topk_weight.shape)
print('-------------------------------------------------------------------------')
print(topk_idx, topk_idx.shape)
输出:
tensor([[0.4110, 0.2948],
[0.3774, 0.2573],
[0.4702, 0.2643],
...,
[0.3643, 0.2254],
[0.4094, 0.2653],
[0.3826, 0.2848]], grad_fn=<TopkBackward0>) torch.Size([16352, 2])
-------------------------------------------------------------------------
tensor([[2, 0],
[2, 0],
[2, 0],
...,
[3, 0],
[0, 1],
[2, 1]]) torch.Size([16352, 2])这样一来,我们就重点关注topK个专家了,那么原先scores为4个专家经过softmax计算后的得分矩阵,即每一行的4个专家得分和为1,现在只取前两名专家的得分,所以需要对前两名专家的得分再归一化,使得前两名专家得分值为1:
denominator = topk_weight.sum(dim=-1, keepdim=True) + 1e-20
topk_weight = topk_weight / denominator
print(topk_weight, topk_weight.shape)
输出:
tensor([[0.5823, 0.4177],
[0.5946, 0.4054],
[0.6401, 0.3599],
...,
[0.6177, 0.3823],
[0.6069, 0.3931],
[0.5733, 0.4267]], grad_fn=<DivBackward0>) torch.Size([16352, 2])1.4 矩阵维度变换
接下来是比较骚气的维度变换操作:
topk_idx_for_aux_loss = topk_idx.view(bsz, -1)
print(topk_idx.shape, '——>', topk_idx_for_aux_loss.shape)
print('-------------------------------------------------')
print(topk_idx_for_aux_loss)
输出:
torch.Size([16352, 2]) ——> torch.Size([32, 1022])
-------------------------------------------------
tensor([[2, 0, 2, ..., 2, 3, 2],
[0, 2, 3, ..., 3, 3, 1],
[1, 3, 3, ..., 2, 1, 0],
...,
[0, 3, 0, ..., 0, 1, 2],
[0, 3, 2, ..., 1, 1, 0],
[2, 0, 2, ..., 1, 2, 1]])这是在做什么操作呢?其实,这中间隐藏了一步,应该为:[16352, 2] —> [32, 511, 2] —> [32, 511*2]。什么意思呢?原先topk_idx被拉平为 [32*511=16352, 2] 了,因为专家的作用域是在token上,那么后面要计算损失时也一定是和token有关的,既然如此,原来的 [32*511=16352, 2] 这种与样本个数(32*511)有关的维度表示形式,就应该变为与token个数(511*2)有关的维度表示形式了。我们可以将topk_idx的维度由32*511行2列还原成(32, 2*511),意味着topk_idx_for_aux_loss表示:有32个样本,每个样本的所有token被拉平为两两专家(topK决定)的形状,即:
[token1—专家top1, token1-专家top2, token2-专家top1, token2-专家top2, ...]
同样,我们把之前计算的scores矩阵也做一些变换:
scores_for_aux = scores # torch.Size([16352, 4])
scores_for_seq_aux = scores_for_aux.view(bsz, seq_len, -1)
print(scores_for_aux.shape, '——>', scores_for_seq_aux.shape)
输出:torch.Size([16352, 4]) ——> torch.Size([32, 511, 4])为什么这么变换呢?后面会用到。
1.5 负载均衡与辅助损失计算
接下来是比较重点的负载均衡操作,是个难点,我会重点介绍一下。先说下为什么会需要负载均衡,在MoE架构中,每个专家都会在训练过程中学习到相应的语义表征能力,我们都知道,神经网络训练的权值调整机理是一个黑盒过程,特别是训练伊始,我们赋予初始权重特征值都是一个随机的过程,当然,这种随机初始化过程遵循一定的分布特点,比如均值分布、高斯分布、正态分布等,虽然如此,每个特征值仍然是一定范围内的随机值,这将导致在训练过程中,哪些位置特征值属于哪个范畴的语义表示也是一个随机的过程。那么就很容易想到,哪位专家学习到哪种表征能力也是很难预测的,这样一来就有这么一种风险:在训练过程中,某些专家可能被过度使用而其他专家被闲置(注意,这是随机的),举个浅显的例子,在楼梯底部放一排敞口瓶,在楼梯顶部往下倒许多乒乓球,等所有球都到达楼梯底部后会发现,一排瓶子中大概率会出现有些瓶子掉进很多球,有些瓶子很少甚至没有。
那么如何缓解这个问题呢?首先想到的就是在专家得分权重的分配上做文章,让那些被选中次数多的专家分配以低一点的权重,让那些被选中次数少的分配以高一点的权重不就行了?比如上面那个例子,让每次掉进球少的那些瓶子换成口大一点的瓶子,掉进球多的换成小一点口径的。那么如何自适应调整这种分配呢?通常对于这类问题,我们首先想到的就是通过损失函数来平衡它们。这就涉及到另一个概念:序列级辅助损失(Sequence-level Auxiliary Loss,可以简称辅助损失)。序列级辅助损失核心目标是实现专家负载均衡,防止 MoE 模型中某些专家被过度使用而其他专家被闲置的问题,这是 MoE 模型中常用的重要技术。
那么该损失函数的数学原理应该长啥样呢?
(1)数学原理
设:
Pi = 模型预测的专家概率分布(softmax 输出)fi = 实际专家使用频率损失函数设计为:
通过最小化 Pi(预测概率)与 fi(实际使用)的乘积和,使得:
- 高使用率专家(fi 大)必须对应低预测概率(Pi 小)
- 低使用率专家(fi 小)可以对应高预测概率(Pi 大)
现在我们通过代码来更深一步理解MoE的负载均衡是如何实现的。
(2)代码实现
为了方便介绍,这里我们假设只有两个样本,每个样本只有3个token:
bsz = 2 # 批次大小
seq_len = 3 # 序列长度
n_routed_experts = 4
top_k = 2 # 每个 token 选择 2 个专家
# 模拟 topk_idx_for_aux_loss(专家选择结果)
topk_idx = torch.tensor([
[[0, 1], [2, 3], [0, 2]], # 第一个样本的 3 个 token 选择的专家
[[1, 3], [1, 1], [3, 2]] # 第二个样本的 3 个 token 选择的专家
]) # shape = (2, 3, 2)
topk_idx_for_aux_loss = topk_idx.view(2, -1) # shape = (2, 6)
# 样本 1 的专家选择展开为:[0, 1, 2, 3, 0, 2]
# 样本 2 的专家选择展开为:[1, 3, 1, 1, 3, 2]现在,我们需要将序列的每个token在4个专家上做一个映射,以便后续计算4个专家对于每个token的贡献度:
scores_for_seq_aux = scores_for_aux.view(bsz, seq_len, -1)
- 输入:
scores_for_aux形状为(bsz * seq_len, n_routed_experts),即每个 token 对各个专家的选择概率。 - 操作:重塑为
(bsz, seq_len, n_routed_experts)。 - 输出示例:
# 假设对于样本 1 的 3 个 token,每个 token 对 4 个专家的选择概率可能是:
[[0.3, 0.2, 0.1, 0.4], # token 1
[0.1, 0.1, 0.6, 0.2], # token 2
[0.5, 0.3, 0.1, 0.1]] # token 3接着我们计算每个样本分别到4个专家的次数:
aux_topk = top_k # 2
ce = torch.zeros(bsz, n_routed_experts)
ce.scatter_add_(1, topk_idx_for_aux_loss, torch.ones(bsz, seq_len * aux_topk)).div_(seq_len * aux_topk / n_routed_experts)这里直接用到了torch中的 scatter_add_ 方法,scatter_add_ 原理:在指定维度(dim=1)上,根据 topk_idx_for_aux_loss 中的索引位置进行累加值。我们通过简单的数据样例来拆解一下上述代码:
- 初始化全零矩阵
ce,该变量存储每个样本所有token共使用的四个专家的情况:
ce = [[0, 0, 0, 0], # 样本 1
[0, 0, 0, 0]] # 样本 2- 创建全 1 张量:
torch.ones(2, 6) 对应每个选择的专家位置标记为 1。
- 执行 scatter_add:
对样本 1 的索引 [0, 1, 2, 3, 0, 2]:
ce[0][0] += 1 # 第 1 次选择专家 0
ce[0][1] += 1 # 选择专家 1
ce[0][2] += 1 # 选择专家 2
ce[0][3] += 1 # 选择专家 3
ce[0][0] += 1 # 再次选择专家 0
ce[0][2] += 1 # 再次选择专家 2
最终样本 1 的 ce:[2, 1, 2, 1]
对样本 2 的索引 [1, 3, 1, 1, 3, 2]:
ce[1][1] += 3 # 专家 1 被选 3 次
ce[1][3] += 2 # 专家 3 被选 2 次
ce[1][2] += 1 # 专家 2 被选 1 次
最终样本 2 的 ce:[0, 3, 1, 2]
- 归一化处理:
.div(seq_len * aux_topk / n_routed_experts)
# 这里 seq_len = 3, aux_topk = 2, n_routed_experts = 4,分母为 3 * 2 / 4 = 1.5,这是我们认为的每个样本选择每个专家的期望值。归一化后:
样本 1: [2/1.5, 1/1.5, 2/1.5, 1/1.5] ≈ [1.33, 0.67, 1.33, 0.67]
样本 2: [0/1.5, 3/1.5, 1/1.5, 2/1.5] = [0, 2.0, 0.67, 1.33]可以这么解释上面两个矩阵,当我们获得了选择每个专家的期望值后,那么根据每个专家的选择的实际数量,可以大概得到实际值和期望值之间的一个差异。后面我们就可以利用这个差异来计算辅助损失了。
接下来就是计算辅助损失啦,通过优化损失,让每个专家的执行负载保持相对平衡。上面已经算出来了 scores_for_seq_aux,即每个 token 对各个专家的选择概率。我们知道,loss是个标量,因此接下来的操作都尽量往合理的,不失优雅的往标量方向压缩。先操作 scores_for_seq_aux:
scores_for_seq_aux_mean = scores_for_seq_aux.mean(dim=1)
示例:
样本 1 平均概率可能为:[0.3, 0.2, 0.27, 0.23] # 示例数据
样本 2 平均概率可能为:[0.0, 0.3, 0.2, 0.5]然后将上文算出来的期望差异分,逐元素去乘以均值化后的专家概率得分矩阵:
ce_multi_scores_for_seq_aux_mean = ce * scores_for_seq_aux_mean
示例:
样本 1: [1.33 * 0.3, 0.67 * 0.2, 1.33 * 0.27, 0.67 * 0.23] ≈ [0.4, 0.13, 0.36, 0.15]
样本 2: [0 * 0.0, 2.0 * 0.3, 0.67 * 0.2, 1.33 * 0.5] = [0, 0.6, 0.13, 0.67]得到了两个样本分别之于4个专家的负载损失矩阵,最后对该矩阵进行求和取平均:
ce_multi_scores_for_seq_aux_mean_sum = ce_multi_scores_for_seq_aux_mean.sum(dim=1)
ce_multi_scores_for_seq_aux_mean_sum_mean = ce_multi_scores_for_seq_aux_mean_sum.mean()
示例:
样本 1 总和 ≈ 0.4 + 0.13 + 0.36 + 0.15 = 1.04
样本 2 总和 = 0 + 0.6 + 0.13 + 0.67 = 1.4
平均值 = (1.04 + 1.4) / 2 = 1.22通产我们会对算出来的loss乘以一个系数α,得到最终的aux_loss:
aux_loss = 1.22 * α总结一下上述计算过程,首先我们先让每个token映射到每个专家所在维度空间,得到的是每个专家之于每个token的贡献率,接着,我们定义了一个向量空间,用于计算损失矩阵,最后,我们将损失矩阵的值压缩成一个标量,作为辅助损失值。
我们回到最初的代码示例,看下输出:
aux_topk = top_k # 2
ce = torch.zeros(bsz, n_routed_experts)
ce.scatter_add_(1, topk_idx_for_aux_loss, torch.ones(bsz, seq_len * aux_topk)).div_(seq_len * aux_topk / n_routed_experts)
print(ce.shape)
print(ce)
输出:
torch.Size([32, 4])
tensor([[0.9863, 0.9785, 1.0254, 1.0098],
[0.9119, 0.9863, 0.9863, 1.1155],
[0.9628, 1.0881, 1.0176, 0.9315],
[0.9628, 1.0098, 0.9628, 1.0646],
[0.9550, 1.1194, 0.9198, 1.0059],
[1.0020, 1.0059, 0.9785, 1.0137],
[0.9706, 1.0333, 0.9706, 1.0254],
[0.9785, 1.0020, 0.9511, 1.0685],
[0.9746, 0.9589, 1.0607, 1.0059],
[1.0568, 0.9550, 1.0059, 0.9824],
[1.0215, 0.9863, 0.9980, 0.9941],
[1.0098, 1.0098, 0.9589, 1.0215],
[1.0372, 0.9706, 0.9198, 1.0724],
[0.9667, 0.9824, 1.0137, 1.0372],
[1.0059, 0.9902, 1.0098, 0.9941],
[0.9002, 0.9354, 1.1076, 1.0568],
[1.0724, 0.9276, 1.0254, 0.9746],
[0.9667, 1.0059, 1.0215, 1.0059],
[1.0215, 0.9902, 0.9863, 1.0020],
[1.0685, 0.9863, 1.0294, 0.9159],
[0.9902, 1.0020, 0.9746, 1.0333],
[0.9785, 0.9746, 1.0176, 1.0294],
[0.9511, 0.9472, 1.0294, 1.0724],
[1.0137, 1.0528, 0.9432, 0.9902],
[0.9706, 1.0333, 0.9511, 1.0450],
[0.9824, 1.0215, 1.0020, 0.9941],
[0.9706, 0.9667, 1.0372, 1.0254],
[0.9472, 0.9941, 0.9980, 1.0607],
[1.0294, 0.9863, 1.0685, 0.9159],
[1.1115, 0.9472, 0.9980, 0.9432],
[0.9824, 1.0098, 1.0333, 0.9746],
[0.9628, 1.0568, 0.9863, 0.9941]])原先scores_for_seq_aux是(32, 511, 4)维的,在第二个维度上(dim=1)也就是511这个维度上取mean均值,也就是对4列中每一列中的511行个元素取mean,最终得到的是(32, 4)维张量:
scores_for_seq_aux_mean = scores_for_seq_aux.mean(dim=1)
scores_for_seq_aux_mean
输出:
tensor([[0.2494, 0.2503, 0.2523, 0.2480],
[0.2448, 0.2470, 0.2453, 0.2629],
[0.2476, 0.2537, 0.2558, 0.2429],
[0.2441, 0.2488, 0.2443, 0.2629],
[0.2487, 0.2616, 0.2422, 0.2475],
[0.2467, 0.2414, 0.2603, 0.2517],
[0.2482, 0.2494, 0.2448, 0.2576],
[0.2433, 0.2457, 0.2518, 0.2592],
[0.2513, 0.2455, 0.2543, 0.2489],
[0.2568, 0.2404, 0.2531, 0.2497],
[0.2541, 0.2434, 0.2502, 0.2522],
[0.2506, 0.2453, 0.2456, 0.2585],
[0.2524, 0.2507, 0.2422, 0.2547],
[0.2476, 0.2502, 0.2459, 0.2563],
[0.2508, 0.2490, 0.2502, 0.2500],
[0.2367, 0.2429, 0.2668, 0.2535],
[0.2545, 0.2422, 0.2511, 0.2522],
[0.2486, 0.2499, 0.2539, 0.2476],
[0.2495, 0.2467, 0.2498, 0.2539],
[0.2590, 0.2498, 0.2532, 0.2380],
[0.2463, 0.2543, 0.2452, 0.2543],
[0.2474, 0.2419, 0.2595, 0.2513],
[0.2468, 0.2435, 0.2550, 0.2547],
[0.2464, 0.2488, 0.2465, 0.2583],
[0.2462, 0.2505, 0.2466, 0.2568],
[0.2465, 0.2504, 0.2544, 0.2486],
[0.2434, 0.2501, 0.2584, 0.2481],
[0.2403, 0.2462, 0.2577, 0.2558],
[0.2434, 0.2504, 0.2551, 0.2510],
[0.2538, 0.2472, 0.2533, 0.2458],
[0.2476, 0.2466, 0.2574, 0.2485],
[0.2487, 0.2453, 0.2561, 0.2499]], grad_fn=<MeanBackward1>)接着就是各种均值计算:
ce_multi_scores_for_seq_aux_mean = ce * scores_for_seq_aux_mean
ce_multi_scores_for_seq_aux_mean_sum = ce_multi_scores_for_seq_aux_mean.sum(dim=1)
ce_multi_scores_for_seq_aux_mean_sum_mean = ce_multi_scores_for_seq_aux_mean_sum.mean()
print(ce_multi_scores_for_seq_aux_mean.shape, '——>', ce_multi_scores_for_seq_aux_mean_sum.shape, '——>', ce_multi_scores_for_seq_aux_mean_sum_mean)
输出:
torch.Size([32, 4]) ——> torch.Size([32]) ——> tensor(1.0007, grad_fn=<MeanBackward0>)最后得到aux_loss:
aux_loss = ce_multi_scores_for_seq_aux_mean_sum_mean * alpha
aux_loss
输出:
tensor(0.1001, grad_fn=<MulBackward0>)OK,以上就是门控网络的训练过程以及辅助损失的计算方法,经过门控计算后,实际上我们得到的有用的是aux_loss(训练阶段),topk_ids(用于专家选择),topk_weight(选择的专家的得分权重)。接下来,就是利用门控计算得到的结果,进行真正的专家计算,就是即将介绍的“专家”网络。
2. 专家网络(MoEFeedForward)
当我们通过门控网络得到了专家权重矩阵topk_weight以及对应的索引矩阵topk_ids,接下来需要带着门控网络给的“导流指南”去找各个专家“说事儿”了。
上文介绍过,MoE中所谓的“专家”其实就是我们熟知的前馈神经网络而已。因此,我们首先定义一个前馈神经网络:MoEFeedForward。
class MoEFeedForward(nn.Module):
def __init__(self):
super().__init__()
self.hidden_dim = 4 * 512
self.hidden_dim = int(2 * self.hidden_dim / 3)
self.multiple_of = 64
self.config_hidden_dim = self.multiple_of * ((self.hidden_dim + self.multiple_of - 1) // self.multiple_of)
self.w1 = nn.Linear(512, self.config_hidden_dim, bias=False)
self.w2 = nn.Linear(self.config_hidden_dim, 512, bias=False)
self.w3 = nn.Linear(512, self.config_hidden_dim, bias=False)
self.dropout = nn.Dropout(0.0)
def forward(self, x):
return self.dropout(self.w2(F.silu(self.w1(x)) * self.w3(x)))我们说了,所谓的“专家”其实就是前馈网络,这里专家路由有4个,即4个专家,那么就初始化4个前馈网络。
num_experts_per_tok = 2
experts = nn.ModuleList([
FeedForward()
for _ in range(n_routed_experts)
])为了方便讲解,我们重新定义一个隐层向量:
hidden_states = torch.randn(32, 511, 512) #随机生成一个隐层向量,作为样例数据
identity = hidden_states
orig_shape = hidden_states.shape
print(identity.shape, orig_shape)
输出:torch.Size([32, 511, 512]) torch.Size([32, 511, 512])与门控网络一样,我们将隐层向量按照batch和序列长度这两个维度拉平,即batch*seq_len:
x = hidden_states.view(-1, hidden_states.shape[-1])
print(hidden_states.shape, '——>', x.shape)
输出:torch.Size([32, 511, 512]) ——> torch.Size([16352, 512])我们将MoE Gate计算出来的topk_id按照选取的topk专家维度拉平,原来的每个token两个专家呈一字排列,实际还是两个元素为一组(同一个token)的idx:
flat_topk_idx = topk_idx.view(-1)
print(topk_idx.shape, '——>', flat_topk_idx.shape)
输出:torch.Size([16352, 2]) ——> torch.Size([32704])按照每个token选择2个专家增加拉平后hidden_states的维度,32个batch一共16352个token,每个token选2个专家,看成16352 * 2个token,每个token有512维特征。可以这么理解,两个token表示的是同一个token在选取的两个专家上的不同特征:
x = x.repeat_interleave(num_experts_per_tok, dim=0)
x.shape
输出:torch.Size([32704, 512])接下来是对专家计算结果的输出:
- 生成一个维度和x一致的空张量y,即
[32704, 512],在专家拉平矩阵(flat_topk_idx)中找到第1、2、3、4个专家的索引(索引分别为0、1、2、3)对应在x中的值,经过前馈网络(专家网络)计算后,赋值给y中同样索引的位置; - 将第一步计算后的y,还原成维度为
[16352, 2, 512]的y1,即一共16352个token,每个token有2个专家,每个专家的特征512维; - 将第二步计算后的y1与topk专家权重矩阵 topk_weight 逐元素相乘,相当于带专家特征的token乘以一个专家权重矩阵,得到y2;
- 第三步计算出来的y2维度仍为
[16352, 2, 512],再将y2在第1维度(即2)上求和,也就是把每个token的两个专家的512个特征值对应两两相加,得到最终的y,维度为[16352, 512]。
y = torch.empty_like(x, dtype=torch.float16)
for i, expert in enumerate(experts):
y[flat_topk_idx == i] = expert(x[flat_topk_idx == i]).to(y.dtype)
y1 = y.view(*topk_weight.shape, -1)
print('y1.shape: ', y1.shape)
y2 = y1 * topk_weight.unsqueeze(-1)
print('topk_weight.unsqueeze(-1).shape: ', topk_weight.unsqueeze(-1).shape)
print('y2.shape: ', y2.shape)
y = y2.sum(dim=1)
y.shape
输出:
y1.shape: torch.Size([16352, 2, 512])
topk_weight.unsqueeze(-1).shape: torch.Size([16352, 2, 1])
y2.shape: torch.Size([16352, 2, 512])
torch.Size([16352, 512])将y的维度还原成原始输入的维度,即[32, 511, 512],此时每个batch中每个token的维度是蕴含了不同专家贡献的特征的,可以理解为由不同专家参与了的token特征:
y = y.view(*orig_shape)
y.shape
输出:torch.Size([32, 511, 512])最后,如果定义了专家共享机制,那么我们就需要对专家参与计算的整体输出再进行共享计算。所谓共享专家,实际上为将y再经过一次前馈计算,使其再一次学习到稠密特征,并进行残差计算,即将学习到稠密特征的隐层向量加上未学习稠密特征前的隐层特征向量,旨在完善整个特征的语义,既包含学习到的稠密特征,又避免丢失原始特征。下方代码的 identity,是我们最初的hidden_states:
shared_experts = FeedForward()
y = y + shared_experts(identity)
y.shape
输出:torch.Size([32, 511, 512])至此,关于MoE的整体结构都介绍完了,包括门控网络和专家网络,上文主要介绍了MoE做训练时的过程,当专家网络做推理时,不同点在于,一是没有了辅助损失,二是最后选择专家的过程:先经过门控网络计算出专家得分矩阵和每个token对应的专家索引矩阵(如果是训练阶段,会用到aux_loss),根据专家索引得到每个专家所负责的token们,这样,我们就可以取到每个专家负责的token的向量了,接着对每个专家负责的token向量进行前馈网络计算(即专家网络计算,目的是让每个token获得所属专家给予的进一步专业知识赋能,让最后的预测更加准确),得到专家输出,最后,还需要对专家输出乘以对应的权重(每个 token 可能被多个专家处理,所以有各自的权重,权重来源于门控网络计算得到的权重矩阵),因为单个token可能被多个专家处理,因此权重需要累加,并返回所有 token 经过各自专家处理并加权后的结果作为最终预测前的输出。接下来介绍一下MoE推理过程。
三、 MoE的推理
MoE的推理发生在专家网络中,即前馈神经网络的推理。如上文介绍,在经过门控网络计算后,我们得到三个输出:topk_ids、topk_weight、aux_loss,其中aux_loss在推理阶段不用。
topk_idx, topk_weight, aux_loss = self.gate(x)假设我们本次推理输入的序列长度为7,那么我们对隐层向量和索引向量的维度做一个变换,便于后续的计算:
x = x.view(-1, x.shape[-1]) # x: [7, 512]
flat_topk_idx = topk_idx.view(-1) # flat_topk_idx: [14,]
flat_expert_weights = topk_weight.view(-1, 1)得到隐层向量x、专家索引矩阵flat_topk_idx加上专家得分矩阵flat_expert_weights,我们就可以进行推理了。
首先,创建一个与输入 x 形状相同的全零张量,用于保存最终每个 token 经过专家处理后的加权输出:
expert_cache = torch.zeros_like(x)
接下来我们要根据专家索引计算每个专家负责的token是哪些,因为我们这里topk为2,因此可以认为每个token由2名专家负责,换个角度,可以把每位token复制成一模一样的2个,然后每一个都对应一个专家,这就是flat_topk_idx,假设它长这样:
flat_topk_idx = tensor([2, 3, 3, 2, 3, 2, 3, 2, 0, 2, 0, 3, 2, 0], device='cuda:0')
该矩阵的含义为:第一个token由专家2和3负责;第二、三、四个token由专家3和2负责;第五个token由专家0和2负责;第六、第七个token分别由专家0和3以及专家2和0负责。
我们算一下每个专家负责token的数量:
第0个专家:3
第1个专家:0
第2个专家:6
第3个专家:5
于是我们可以得到专家使用频次矩阵:[3, 0, 6, 5],该矩阵有4列,表示4个专家的使用频次,同时也能得到每个专家能负责的子序列在整个序列中的位置,上述过程我们可以通过一下方法直接计算:
tokens_per_expert = flat_topk_idx.bincount().cpu().numpy().cumsum(0)
这样我们得到的 tokens_per_expert 是一个 [3, 3, 9, 14] 的矩阵,该矩阵表示:专家0负责的序列长度为3,则该序列的最后一个token(包括上述所说的同一个token的2份复制)索引位置应为3,而专家1由于使用频次为0,则它所表示的最后一个索引位置不变,仍然为3,到专家2时,由于它使用频次为6,且前面有3个token,因此它所表示的最后一个索引位置为9,同理专家3为14。
由于tokens_per_expert中的元素是按照从0到3这样的专家顺序来排列的,因此我们为了能和它保持一致,也需要对flat_topk_idx做一个排序,也按照专家编号的顺序排列:
idxs = flat_topk_idx.argsort()
上述操作返回的idxs的含义为:flat_topk_idx经过升序排序后,排序后的各个元素在原未排序的flat_topk_idx中的索引位置。
因为flat_topk_idx = [2, 3, 3, 2, 3, 2, 3, 2, 0, 2, 0, 3, 2, 0],排完序后为:[0, 0, 0, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3],则idx应为:[10, 8, 13, 7, 12, 5, 0, 9, 3, 2, 11, 1, 4, 6]。需要注意的是,原向量中存在重复元素,比如0,那么排序后,同样是0的位置应该在原向量怎么安排呢?我实验过,当你将张量放进CUDA中,排序为[10, 8, 13, 7, 12, 5, 0, 9, 3, 2, 11, 1, 4, 6],当放进CPU中,排序为[ 8, 10, 13, 0, 3, 5, 7, 9, 12, 1, 2, 4, 6, 11],也就是说,排序后元素在未排序张量中的索引选取,取决于系统底层的计算方式,因此这里不用纠结了,不管哪种方式,也不影响。
由于idxs是针对14个带复制token的情况来说的,而我们实际的token数也就是7个,因此归根结底我们还是需要将其原有的位置索引计算出来,因为我们topk取的是2,因此还原token的位置索引可以:
token_idxs = idxs // 2
这样一来,我们就能看到原来真实的token_idxs为:[5, 4, 6, 3, 6, 2, 0, 4, 1, 1, 5, 0, 2, 3],即原来所谓的专家0负责第10、8、13个token,实际上是负责的第5、4、6个token,以此类推。
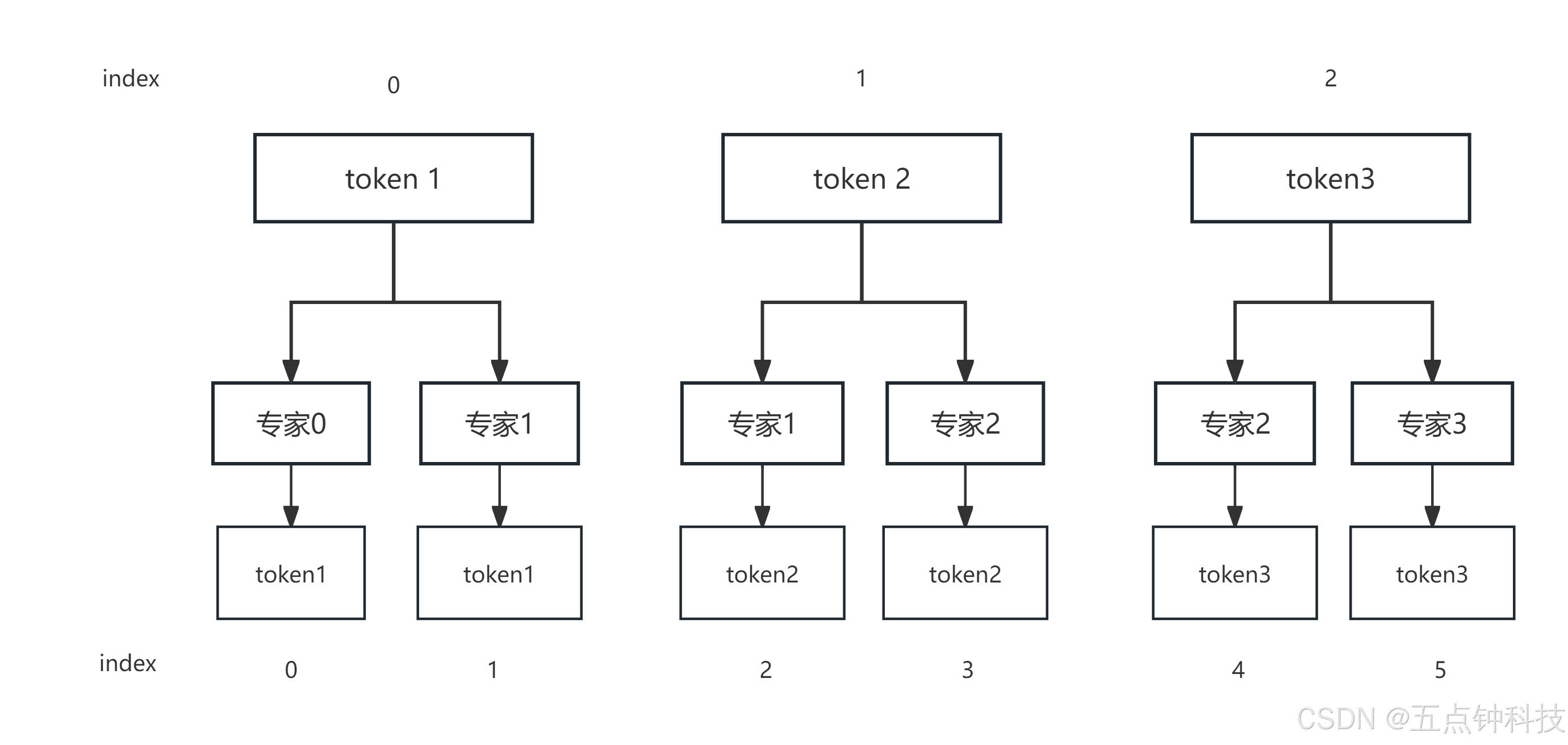
接下来,就可以遍历 tokens_per_expert([3, 3, 9, 14]) 了,第一个3,表示专家0所负责token子序列的终止索引,对应token_idxs的5、4、6,即token_idxs[0: 3];专家1不负责任何token,跳过;专家2对应的token_idxs为[3, 6, 2, 0, 4, 1],即token_idxs[3: 9];同理专家3负责的token的id为[1, 5, 0, 2, 3]。
现在我们得到了每个专家负责的token的索引集合,通过该集合,我们可以回到原序列中取到对应的token向量,对每个索引集合exp_token_idx:
expert_tokens = x[exp_token_idx]
根据每个索引集合对应的专家,进行专家网络计算:
expert_out = expert(expert_tokens)
假设此时遍历到专家2,则得到一个[6, 512]的矩阵向量,得到的专家输出需要乘以专家得分权重矩阵:
expert_out.mul_(flat_expert_weights[idxs[start_idx:end_idx]])
因为每个token可能由不止一个专家负责,因此最终的每个token的专家计算特征向量应该为累加的,并且,因为我们的token根据专家编号进行了重排,所以最终的输出应该将token顺序还原,因此,我们可以用 scatter_add_ 完成上述操作:
- 定义一个存储缓存向量,维度与x保持一致:
expert_cache = torch.zeros_like(x)
- 在 expert_cache 中,找到与 exp_token_idx 中所表示的索引对应的位置进行expert_out赋值:
expert_cache.scatter_add_(0, exp_token_idx.view(-1, 1).repeat(1, x.shape[-1]), expert_out)
比如此时exp_token_idx为专家2的[3, 6, 2, 0, 4, 1]token集合,它已经计算出来expert_out,那么就找到expert_cache对应索引位置为3, 6, 2, 0, 4, 1的位置,将expert_out赋值。当下一批token集合来了,如果存在重复的token索引,比如专家3也负责了第3个token,那么就把expert_cache中第3行的值进行累加。
以下是MoE推理方法的完整代码:
def moe_infer(self, x, flat_expert_indices, flat_expert_weights):
expert_cache = torch.zeros_like(x)
idxs = flat_expert_indices.argsort()
tokens_per_expert = flat_expert_indices.bincount().cpu().numpy().cumsum(0)
token_idxs = idxs // self.config.num_experts_per_tok
# 当tokens_per_expert = [6, 15, 20, 26],tokens_per_expert.shape[0]即为专家数量(此时为4)
# 且token_idxs = [3, 7, 19, 21, 24, 25, 4, 5, 6, 10, 11, 12...] 时
# 意味token_idxs[:6] -> [3, 7, 19, 21, 24, 25]这6个位置属于专家0处理的token(每个token有可能被多个专家处理,这取决于num_experts_per_tok)
# 接下来9个位置token_idxs[6:15] -> [4, 5, 6, 10, 11, 12...]属于专家1处理的token...依此类推
for i, end_idx in enumerate(tokens_per_expert):
start_idx = 0 if i == 0 else tokens_per_expert[i - 1]
if start_idx == end_idx:
continue
expert = self.experts[i]
exp_token_idx = token_idxs[start_idx:end_idx]
expert_tokens = x[exp_token_idx]
expert_out = expert(expert_tokens).to(expert_cache.dtype)
expert_out.mul_(flat_expert_weights[idxs[start_idx:end_idx]])
expert_cache.scatter_add_(0, exp_token_idx.view(-1, 1).repeat(1, x.shape[-1]), expert_out)
return expert_cache通过以上介绍,我们已经把MoE的推理过程搞清楚了,大概过程就是:找到每个专家负责的token们,取出这些token们的向量,进行专家网络计算,计算出的专家结果,乘上专家权重,得到最终的专家参与的token向量。最后一个问题,MoE的这一过程在整个大模型的训练和推理中体现在哪里?
我们看上一篇 博客 中的MiniMindBlock实现:
class MiniMindBlock(nn.Module):
def __init__(self, layer_id: int, config: LMConfig):
super().__init__()
self.n_heads = config.n_heads
self.dim = config.dim
self.head_dim = config.dim // config.n_heads
self.attention = Attention(config)
self.layer_id = layer_id
self.attention_norm = RMSNorm(config.dim, eps=config.norm_eps)
self.ffn_norm = RMSNorm(config.dim, eps=config.norm_eps)
self.feed_forward = FeedForward(config) if not config.use_moe else MOEFeedForward(config)
def forward(self, x, pos_cis, past_key_value=None, use_cache=False):
h_attn, past_kv = self.attention(
self.attention_norm(x),
pos_cis,
past_key_value=past_key_value,
use_cache=use_cache
)
h = x + h_attn
out = h + self.feed_forward(self.ffn_norm(h))
return out, past_kv从代码中可以看出,在每一层的最后一层前馈神经网络计算部分,我们使用了MoE,至此,我们开篇提出的所有问题都解答完毕。
四、总结
我们总结一下开篇的几个问题:
1. 什么是MoE?
MoE本质上其实还是前馈神经网络,只不过对传统的前馈神经网络多做了一些token级别的计算,增加了一个门控层,用于操作专家的选择问题。
2. 它的结构是啥样的(组成部分)?它是怎么实现的(原理)?
它由门控层和专家网络组成,门控层其实无非就是一些矩阵的计算,输出专家选择矩阵,其实就是专家的索引矩阵,还输出了专家得分矩阵,其实就是给不同专家赋予不同权重,让每个token都能更好的被负责的专家所表示。如果是训练阶段,还输出一个辅助损失,用来平衡专家的选择频率;专家网络是前馈神经网络,N个专家就有N个前馈神经网络。
3. 它是怎么用的?用在大模型的哪里?
当成前馈神经网络正常用,用在Transformer中最后一个前馈层。




























 1232
1232

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










