手写VIO第4章--基于滑动窗口算法的 VIO 系统：可观性和 一致性--笔记

0. 内容

由于我们是要做一个实时的定位系统，而不是SfM那种离线的三维重建的工作，所以需要在滑动窗口中不断地添加新数据以及删除旧数据，而前者可以把所有数据放在一个BA中求解。

1. 从高斯分布到信息矩阵

SLAM问题的建模，MAP->MLE->LSP，我们只关心最大后验分布的那个点


这个${\Sigma }^{-1}$表示的是每次观测所占的权重，可调，也有方法可以动态地估计出。${\Sigma }^{-1}$，可以看论文。
之前的正规矩阵中没有写${\Sigma }^{-1}$是因为当时设为单位阵，实际上中间是有个权重矩阵${\Sigma }^{-1}$的

如图中的绿框

协方差对角线元素为对应下标的元素的协方差，由于是零均值，所以$\mu =0$。
右边表示x和y之间的相关性情况，如果是严格线性的，那点的分布就是一条直线，但是明显不是严格线性的，即协方差矩阵非对角元素不为0。
计算方法参考下图：


所以零均值的分布，$Cov(x_i{x}_j)=E(x_i{x}_j)-E(x_i)E(x_j)=E(x_i{x}_j)$（下面式(11)用到）

本节课主题：如何往窗口中加新的变量以及把旧的变量删掉。

下面的例子有助于我们理解SLAM问题中的信息矩阵$H$的组成。

1.1 例子1

对于(11)，此处是写为了标量形式，回顾第3章3.3节的结论：

(11)的结果写成矩阵形式就是${\omega }_1{\sigma }_2^2{\omega }_1^T+{\sigma }_1^2$

求协方差矩阵的逆，可以直接对(13)求逆，但是麻烦，还可以通过计算联合高斯分布来得到协方差矩阵的逆：

有$条件=\frac{联合}{边缘}，上述有向无环图箭头的起点表示条件，终点表示结果。故$（14）由来：$$p(x_1,x_2,x_3)=p(x_1,x_3|x_2)\ast p(x_2)=p(x_1|x_2)\ast p(x_3|x_2)\ast p(x_2)$$
不清楚为什么(14)可以这样写，本来从协方差矩阵中可以看出$x_1,x_3$不是相互独立的，但是写出来的感觉好像是独立的。（这个问题在下面有解释）
然后就是通分，结合高斯分布的形式：

可以看出协方差矩阵的逆就是中间的那个矩阵。

回答上面的问题，从${\Sigma }^{-1}$可以看出，${\Sigma }_{13}={\Sigma }_{31}=0$，代表在变量$x_2$的条件下，$x_1,x_3$是相互独立的。即当房间2的温度($x_2$)确定时，房间1，3的温度($x_1,x_3)$互不影响，相互独立。所以其实上面推导(14)时已经是使用了“在$x_2$的条件下，$x_1,x_3$相互独立”这个结论。

协方差矩阵和信息矩阵的符号所代表的含义不同。

1.2 例子2

同样地，$联合=条件\ast 边缘$，$x_1,x_3$独立，(18)推导:
$$p(x_1,x_2,x_3)=p(x_2|x_1,x_3)\ast p(x_1,x_3)=p(x_2|x_1,x_3)\ast p(x_1)\ast p(x_3)$$

${\Sigma }_{13}=0$但是$({\Sigma }^{-1}{)}_{13}>0$，表示当$x_2$确定时，$x_1,x_3$呈负相关，对应实际问题就是：房间2中的温度一定时，房间1温度高点的话，房间3温度就要低一点才能保证房间2中温度一定。

上面的节点和边是一个有向无环图，是贝叶斯图论中的东西（之前有博士师姐研究这个的，每次听她汇报都一脸问号，压根听不懂）。

1.3 例子1的拓展

如果例子1中没有$x_3$，那么在$\Sigma ,{\Sigma }^{-1}$中直接把有关$x_3$的变量置为0即可：

但是实际中我们不知道$\Sigma ,{\Sigma }^{-1}$由哪几项构成，也就无法去掉为0的项，这时需要引入其他的方法来帮助我们找出这些项：marginalization(边缘化)和Schur’s complement(舒尔补)。

1.4协方差矩阵和信息矩阵小结

1. 协方差矩阵$\Sigma$非对角元素>0则代表对应元素正相关，信息矩阵${\Sigma }^{-1}$中非对角线元素<0代表两元素正相关，>0则是负相关(毕竟是求逆)。
2. 协方差矩阵表示两个变量之间的关系，而信息矩阵则表示两个变量在某种特定条件下的关系。

2. 舒尔补应用

将矩阵M变为上三角或者下三角矩阵，得到的$\Delta A$叫做舒尔补

舒尔消元便于求解方程$H\Delta x=b$，$H=J^{T}J$是稀疏的，把路标点信息边缘化到相机位姿中，求解出相机位姿后再求解位姿。

这部分内容可以复习14讲后端1中关于稀疏化和边缘化的部分，看完例子之后再来理解这里的内容会比较容易。
如果是VSlam，下面的$x$可以看做是由相机位姿(a，se(3))和路标点(b,$R^3$)组成，K就是$J^{T}J$（可能VIO会有些差别）

2.1 边缘概率P(a), 条件概率P(a|b)的协方差矩阵

(31)严格来说应该减去$[a,b{]}^T$的期望，但是这里不怎么关注期望

将式(29)带入得，可以整理为只与a,b有关的部分，就分解为边缘概率和条件概率：

(33)是全概公式

正规方程也可以写为以下形式(vins-mono里面有这个，因为ceres不接受传信息矩阵，所以构造残差时需要将信息矩阵考虑进去，所以对信息矩阵进行LLT分解，与现有residual构建新的residual，见博客开头的介绍)

但是实际上信息矩阵的左上角的块不一定好求，因为$A^{-1}$不一定好求，左上角的块不仅仅跟$A^{-1}$有关，见(36)

边缘概率实际中是相机位姿的概率，条件概率是在相机位姿的条件下看到的路标点的概率。

2.2 P(a), P(a|b)的信息矩阵

已知信息矩阵${\Sigma }^{-1}$，可以看出左上角矩阵块${\Lambda }_{aa}$(只是记法，不是$\mathbf{A}$的信息矩阵)不只是和$A^{-1}$有关，但是对边缘分布$P(a)$，$$\begin{gathered} \Sigma =cov(P(a))=\mathbf{A} \\ {\Sigma }^{-1}=info(P(a))={\mathbf{A}}^{-1} \end{gathered}$$ 的协方差就是$\mathbf{A}$，$P(a)$的信息矩阵就是${\mathbf{A}}^{-1}$，给了信息矩阵${\Sigma }^{-1}$，如何求出边缘分布的信息矩阵${\mathbf{A}}^{-1}$呢？

对(36)高斯消元可得${\mathbf{A}}^{-1}$

对应到1.3的例子，去掉$x_3$时，求$P(x_1,x_2)$的信息矩阵，即求边际概率的信息，直接套用(38)，如下式(39)，$K_2^{-1}$即为$P(x_1,x_2)$的

信息矩阵，此处marg掉$x_3$，要求$P(x_1,x_2)$的联合分布的信息矩阵，那就是只能把$(x_1,x_2)$的联合当做边界分

布，对应表中就是求边界分布的信息矩阵，套用相应的公式。

2.1 总结

表格说明：

1. 表格第一行对应(33)(34)，第二行对应(37)(38)，${\Lambda }_{bb},{\Lambda }_{ab}$等是矩阵块的记法，不是信息矩阵。

2. 表格这套公式假设$P(a)$是边际概率，$P(b|a)$是条件概率，实际操作时把被marg掉的变量移到${\Lambda }_{bb}$的位置，再求边际概率。

总结：
3. 在SLAM中，舒尔补主要是利用H矩阵的稀疏性来求解SLAM问题：
1. 用于求解SLAM问题，由于H矩阵是稀疏的，所以我们可以先用Shur消元，求出pose的$\Delta x$，然后再求出landmark的$\Delta x$；而Shur消元的方法就是Marginalization，将路标点landmark信息marg到pose中。
2. 用在滑动窗口算法中，将旧的信息丢掉，我们也是通过舒尔补的形式将一部分信息给marg掉，且通常是操作边缘概率的信息矩阵。
4. 上表。
5. 可从推导的角度来理解上述矩阵：
由联合协方差矩阵只能推出边际和条件分布的协方差矩阵，由信息矩阵只能推出信息矩阵。

3. 滑动窗口算法

3.1 算法介绍

把被marg的变量作为${\Lambda }_{bb}$，然后使用表格中的公式计算边际概率的信息矩阵。
这个去掉旧变量引起信息矩阵变化的过程叫做"fill-in"

如果直接丢弃，则${\xi }_1$的行和列都去掉，剩下的不变：

KF维护的是均值和协方差矩阵，这里marg维护的是信息矩阵（information filter），但是实际上KF和information filter是对偶的。

上面是实际的滑动窗口的marg的实例，当新的$x_{t+1}$进来之后，跟$x_t$产生关系，但是当$x_t$被marg掉之后，为了保证$x_t$的信息，剩下的信息矩阵会变得稠密，原来独立的变量可能会变得相关。
高翔补充：因为marg掉某个位姿可能会使信息矩阵变稠密，所以如果某个路标点仍然在最新的窗口中，可以尝试把要删掉的key frame中对该landmark的观测删除，假装该keyframe没有看到该landmark，避免information matrix变得过于稠密，影响求解速度，当然，也存在优化精度和速度的trade-off，因为该landmark可能是需要被优化的。

3.2 滑动窗口中的FEJ算法

marg之后，增加新变量${\xi }_7$，与${\xi }_2$有关，导致${\xi }_2$的information matrix由两部分构成，存在风险：由于线性化点可能不同，导致information matrix中多加了信息，改变了零空间。

marg之后，生成的${\Lambda }_p和b_p$是$x_r$的先验，实际上，我们marg时不是直接操作的information matrix，操作的是information matrix、Jacobian、residual的组合体，即构建LSP时定义的$J^T{\Sigma }^{-1}J$和$J^T{\Sigma }^{-1}r$，所以我们根据${\Lambda }_p和b_p$分别反解出residual和jocabian，但是由于此jocabian中有变量已经被marg掉，不存在了，所以这个jocabian也不变了，会导致对剩下的变量的雅可比有两部分组成：

• ${\Lambda }_p$中关于$x_r$的jocabian
• 更加新的线性化点处的$\Lambda$中关于$x_r$中部分变量的jocabian
  这样就可能导致零空间发生变化。

ceres一般都是定义残差，给Jocabian，而g2o可以传传inforamtion matrix。

新的LSP，新的b和$\Lambda$由两部分组成：先验 和 除了与被marg变量无关的量（不明白为什么是减号）。

零空间是7维：6自由度pose+1尺度scale

上图1代表全局的观测，那么最优解就是$xy=1$，但是当sliding windows时我们只能获取部分观测，图2一个，图3一个，且图2和图3的线性化点都不同，图3时，图2已经被marg掉了，他的jacobian不会再变化了，于是即出现了图4的情况，导致本来最优解是$xy=1$的，现在变成了确定的最优解了。

对于线性空间里面，简单理解就是单射，矩阵不满秩就会有零空间（即矩阵不满秩就会有无穷多解，矩阵满秩才会有唯一解）。非线性的时候，不能说是单射？（说的不是很清楚）SLAM中即状态量不同时cost不同。（为什么上图4中的变量变为是可观的？如y=1，x可以取很多不同的值?）
暂且简单理解为单射吧。只能一对一，不能多对一。

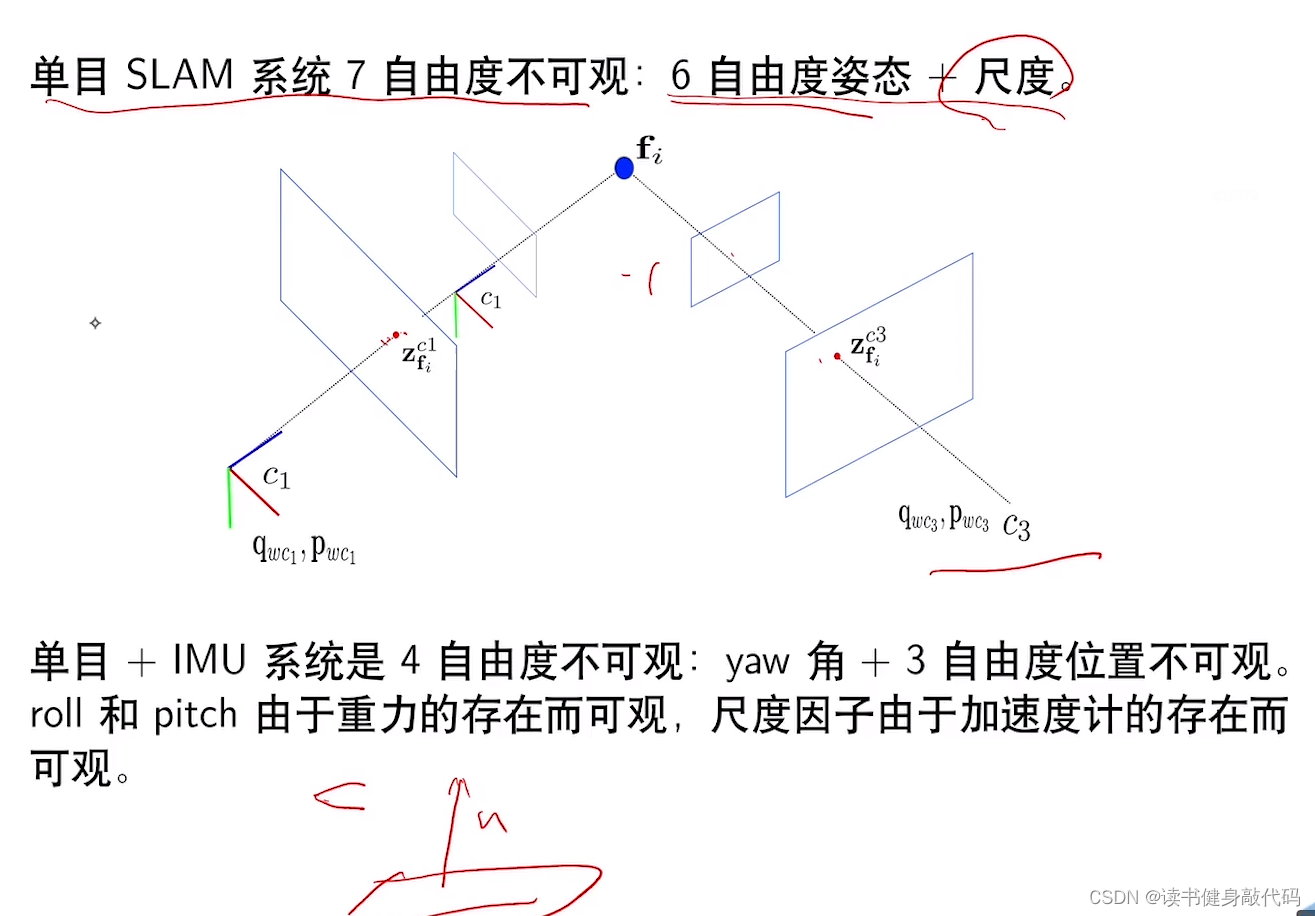
• 单目VSLAM系统，pose不可观，尺度也不可观（在广州和上海的万达拍同一个特征点不知道在哪，离远点和近点拍也分辨不出来），简单理解，哪个自由度不可观就是指多个该自由度的输入都能得到相同的输出。
• 单目+IMU：由于重力，roll，pitch可观，由于acc可提供实际的m制单位，所以scale可观。

零空间问题的解决方法：FEJ算法。

解决方法：在做marg时，相关的landmark在求jacobian时，线性化点必须相同。

3.3 sliding windows总结

1. sliding windows目的是为了控制优化问题的维度，在迭代过程中存在删除旧数据(marg)和加入新数据的操作，marg旧数据会把旧数据的信息通过information matrix传递给窗口中剩余的数据，可能使得原来不相关的数据之间出现了关系（出现了边），即在information matrix的非对角线出现了非零值；
2. 在marg的过程中，由于删掉了部分信息（如${\xi }_1$），剩余变量$x_r$，导致information matrix发生了变化（$x_r$中存在与${\xi }_1$相关的其他变量，后续在求这些变量的jacobian时，由于线性化点不一样，导致零空间发生了退化），零空间退化后，不可观的变量变成了可观的，为了解决此问题，使用了FEJ方法，求$x_r$中变量的Jacobian时，只使用marg时的线性化点的值来求，避免了零空间退化的问题。

4. 第5章相关内容

尝试了一下知乎的编辑器 https://zhuanlan.zhihu.com/p/659499854

5. 待看文献：

1&2.

3.

4.

5.

6.

7.

8.

OKVIS是什么论文

6. 作业

博客链接