
http://blog.three-eyed-games.com/2018/05/12/gpu-path-tracing-in-unity-part-2/
上一章我们使用的光线追踪方法是递归式光线追踪(Whitted-style Ray Tracing),我们假设每次光线都是表面法线进行的完美反射,所以他可以很好的展现光滑物体表面的反射效果。但是现实生活着并不是所有物体都是非常光滑的,这种方法无法展现物体之间相互作用的漫反射,还有物体的光泽。所以这一章我们把它改成蒙特卡洛路径追踪(Monte Carlo Path Tracing)。
相关概念看这篇文章。
路径追踪=光线追踪+蒙特卡洛方法
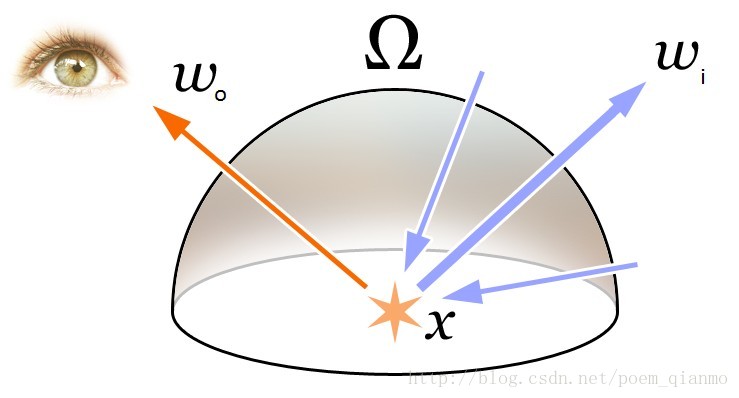
渲染方程
:碰撞点X在w方向的出射光
:出射光的自发光贡献
:Ω=法线方向的半球面,这个积分的意思就是综合这个半球面所有可能方向的入射光对这个指定的出射光线的贡献。
:双向反射分布函数BRDF
:入射光和表面法线的夹角cos值,夹角越大,值越低,出射光强度越弱,因为夹角越大大,一束光线越容易分散
:入射光,这个值就是前一个碰撞点用渲染方程得到的出射光,如此递归直到结束。
蒙特卡洛积分
我们无法明确的知道入射光来自哪些方向,所以我们使用蒙特卡洛方法在所有可能的方向中随机采样,我们采样的越多,越接近正确的结果。
:随机的一次采样的结果
:这种采样情况发生的可能性,不容易出现的采样情况会有更大的权重,以此来平衡每次采样对最终结果的贡献度,这样可以更快的趋向正确的结果。
这里我们先假设光线在半球面的各个方向的入射几率都是相同的,也就是说。(单位半球的表面积为2π)。
先前的渲染公式就可以修改成如下:
前一章为了抗锯齿,我们使用addshader对多次采样进行平均取值,正好完成了公式中的
这部分,但是因为OnRenderImage中的destination纹理精度为R8G8B8A8的类型,而我们希望的是RGBAfloat的精度,所以我们要再创建一个贴图用于来回倒,至于为什么要这样一个精度后面有提到。
又是上一条光线的递归结果(也就是代码中的energy),
所以我们修改的就是绿色的这个部分。
随机采样
随机值的获取:
float2 _Pixel;//像素位置 float _Seed;//随机种子 float rand() { float result = frac(sin(_Seed / 100.0f * dot(_Pixel, float2(12.9898f, 78.233f))) * 43758.5453f); _Seed += 1.0f; return result; }根据随机值在指定半球得到一条随机方向
球坐标系转直角坐标系:
x=rsinθcosφ.
y=rsinθsinφ.
z=rcosθ.
float3 SampleHemisphere(float3 normal) { // 每个方向被采样的几率都一样 float cosTheta = rand(); float sinTheta = sqrt(max(0.0f, 1.0f - cosTheta * cosTheta)); float phi = 2 * PI * rand(); float3 tangentSpaceDir = float3(cos(phi) * sinTheta, sin(phi) * sinTheta, cosTheta); // 传至世界空间 GetTangentSpace就是计算切线矩阵,右乘就是逆 return mul(tangentSpaceDir, GetTangentSpace(normal)); }
漫反射部分
Lambert BRDF:
所以渲染方程变为(忽略自发光):
// Diffuse shading
ray.origin = hit.position + hit.normal * 0.001f;
ray.direction = SampleHemisphere(hit.normal);
ray.energy *= 2 * hit.albedo * sdot(hit.normal, ray.direction);
return 0.0f;float sdot(float3 x, float3 y, float f = 1.0f)
{
return saturate(dot(x, y) * f);
}镜面反射部分
Phong BRDF:
修改渲染方程:
图为α=15,入射光为45度(左侧斜线)时的图像,红色是各个方向的出射光最终得到的值,可以看到出射光方向等于反射方向(右侧斜线)时值最大,约为,一旦偏离这个方向,值就会迅速降低。

采样优化
我们从金属物体的角度看一下:一般来讲非金属有albedo,金属有specular,所以albedo很高specular就很低,在原文的代码中,如果是金属,那么albedo直接定义为0.04,相当于没有,所以我们可以把渲染方程式中的漫射部分忽略,专注于高光部分,要记住,在我们随机采样的过程中,我们仍然是有可能得到距离完美反射方向偏差极大的一个采样方向,这明显是一个我们可能性很小的采样方向,所以这次采样带来的贡献度会非常低,这次采样相当于浪费了,而如果采样方向和匹配时,PhoneBRDF将会返回一个大于1的值,这样就可以补偿0值的采样。我们α=15是,值就是
了,下面是平滑度和α值之间的转换,可想而知高光滑度的物体,方向匹配时返回的BRDF会有多大了。还记得前面我们将贴图的格式设为RGBAfloat吗,这样我们就可以存储(相对于颜色)大于1的值了。
float SmoothnessToPhongAlpha(float s) { return pow(1000.0f, s * s); }这样就出现了一个问题,靠近反射方向会得到非常大的BRDF值,远离又会得到非常低的BRDF值,但我们又是完全平均的随机采样,这就会产生非常大的方差。我们可能会连续获得低贡献度的采样,需要更多的采样去补偿才能平衡最终的结果。
表现在画面上就是会出现很多的噪点。
要解决这一点,我们先要把漫反射和镜面反射分开。因为漫射本来就可能来自任意方向,所以原来的随机采样方向就合理,但是镜面反射的方向就更加集中在理想的反射方向,这里我们先假设就让他等于反射方向。
//计算反射和漫射的概率 energy=颜色三个分量的平均值 hit.albedo = min(1.0f - hit.specular, hit.albedo); float specChance = energy(hit.specular); float diffChance = energy(hit.albedo); float sum = specChance + diffChance; specChance /= sum; diffChance /= sum; //决定这次采样时反射还是漫射 float roulette = rand(); if (roulette < specChance) { // 反射 ray.origin = hit.position + hit.normal * 0.001f; //我们先假设都是完美的反射 ray.direction = reflect(ray.direction, hit.normal); ray.energy *= (1.0f / specChance) * hit.specular * sdot(hit.normal, ray.direction); } else { // 漫射 ray.origin = hit.position + hit.normal * 0.001f; ray.direction = SampleHemisphere(hit.normal); ray.energy *= (1.0f / diffChance) * 2 * hit.albedo * sdot(hit.normal, ray.direction); } return 0.0f;float energy(float3 color) { return dot(color, 1.0f / 3.0f); }
结果大概是这样,每个金属球都有着绝对光滑的反射面

重要性采样(Importance Sampling)
现实中不可能每个物体都是光滑的,会完美的反射光线,我们还是得允许我们的反射光线方向能在限定范围内随机获取。
先前的渲染公式我们让蒙特卡洛积分中的,让所有方向可能性都相同,所以我们更多的依赖BRDF值来作为权值的调整,补偿或调和平均的采样值,我们有可能经常计算到贡献率很低的方向采样。我们应该让贡献度高的采样结果出现的多一点,贡献度低的采样出现的几率第一点。也就是说我们把采样的权值转移到不同方向采样的频次上面,通过除以不同的可能性,让每次采样的贡献度趋于平等
比方说我们现在有两个采样方向分为两个区域,两个区域占最终的贡献分别为8和2 ,最终结果是10
如果我们平均随机采样 也就是每个方向都有0.5的几率
理想状态下10次采样:(16+16+16+16+16+4+4+4+4+4)/10=8+2
采样蓝色提供1.6的贡献,采样红色却只有0.4的贡献,也就是说你采样4次红色的价值才等于采样一次蓝色区域的方向。
如果我们知道了蓝方的贡献值更高,所以让选择方向时,按贡献的大小分配比例。也就是0.8和0.2
理想的10次采样:(10+10+10+10+10+10+10+10+10+10)/10=8+2
无论采样红色还是蓝色都是平均的1贡献,无论采样红色还是蓝色,价值都一样,
当然我们不可能让贡献度和采样可能性完全匹配,但是有个近似值也足够了,就比方说0.7和0.3
理想的10次采样:(11.4+11.4+11.4+11.4+11.4+11.4+11.4+6.66+6.66+6.66)/10=8+2
采样蓝色1.14 采样红色 0.66,会比完全随机采样要平均一点,2次红色相当于一次蓝色
写到这突然觉得我可能想复杂了,总而言之,高贡献度的区域值得拥有更多的采样来获得更准确的结果,低贡献度的区域采样的少一点,准确度低一点也不要紧,对画面的影响不大。
非统一分布采样
float3 SampleHemisphere(float3 normal, float alpha)
{
// alpha值越高,方向越集中分布在法线附近 0=平均分布 1往上就是phone的指数了
float cosTheta = pow(rand(), 1.0f / (alpha + 1.0f));
float sinTheta = sqrt(1.0f - cosTheta * cosTheta);
float phi = 2 * PI * rand();
float3 tangentSpaceDir = float3(cos(phi) * sinTheta, sin(phi) * sinTheta, cosTheta);
return mul(tangentSpaceDir, GetTangentSpace(normal));
}这样修改后每个方向被选到的几率为,将它带入
我们就可以得到新的渲染公式
Lambert BRDF
我们将漫射的α设为1,这样,渲染公式中的
可以刚好相互抵消
Phone BRDF

把
和
抵消掉了???
自发光
相当于新的光线并入这条光路,所以直接return自发光颜色
hit.albedo = min(1.0f - hit.specular, hit.albedo);
// 计算漫反射和镜面反射的几率 energ()=颜色三个分量的平均值
float specChance = energy(hit.specular);
float diffChance = energy(hit.albedo);
float sum = specChance + diffChance;
specChance /= sum;
diffChance /= sum;
// 确认这是光线追踪是漫反射还是镜面反射
float roulette = rand();
if (roulette < specChance)
{
// 镜面反射
float alpha = SmoothnessToPhongAlpha(hit.smoothness);
ray.origin = hit.position + hit.normal * 0.001f;
ray.direction = SampleHemisphere(reflect(ray.direction, hit.normal), alpha);
float f = (alpha + 2) / (alpha + 1);
ray.energy *= (1.0f / specChance) * hit.specular * sdot(hit.normal, ray.direction, f);
}
else
{
// 漫反射
ray.origin = hit.position + hit.normal * 0.001f;
ray.direction = SampleHemisphere(hit.normal,1.0f);
ray.energy *= (1.0f / diffChance) * hit.albedo;
}
return hit.emission;























 2万+
2万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








