刘二大人《PyTorch深度学习实践》笔记 + 作业

课程链接

1. Overview

人类智能（Human Intelligence）

推理 infer

预测（prediction）：实体——抽象概念

而 machine learning 就是把推理的大脑变成算法

How to develop learing system？

基于规则的算法（人工智能程序）：依赖于规则，需要非常专业的背景知识来制定规则，构建知识库。如果是很复杂的目标，是很难把规则做通的，肯定会漏一些，导致算法有缺陷。规则只会越来越多，越来越庞大，直到人类无法维护。注意，基于规则的并不是学习系统。最出名的可能是 SVM。

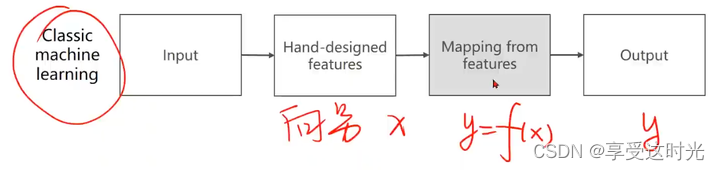
经典机器学习算法：人工设计提取特征，把输入（图片，语音，文字）变成一个向量，向量和输出之间要建立一个映射函数。 y=f(x)。

表征学习：希望 features 的提取方法，也能自己学习出来。
features提取 是一个单独的步骤，用一些特殊的算法，从一个很复杂的非结构输入数据里面提取出一个向量，让把向量输入到 mapping from features里面。
feature提取是无标签的，无监督学习方法。mapping from features 学习器是有标签的，所以要分开训练的。

为什么要特征提取呢？减少成本。

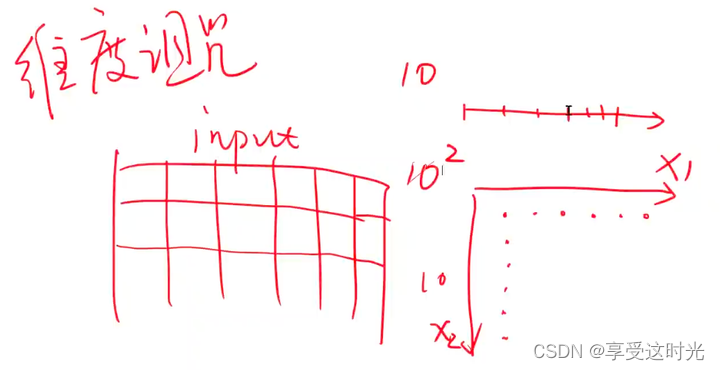
维度诅咒：如果输入的每一条数据样本的feature数量越多，对整个样本的数量需求就越多。

首先统计里面，大数定律：采样越多，那么和数据的真实分布就越贴近。

• 如果数据只有一个 feature，一维空间采样，10个样本，密度可能就够了。
• 如果数据有两个 feature，二维空间。采样的时候，行和列就都得达到10。也就是100个点，才能够满足大数定律，才能够表示原始数据的分布。
• 如果数据有三个 feature，三维空间，如果要保持密度，就需要 $10^3$。
• 如果数据有N个维度呢？就需要$10^N$。
• 所以维度越高，对数据的需求就越大。而收集数据本身工作量非常大，成本也非常大，数据集是很贵的。
  

所以我们希望能不能维度N较低小一点。还希望把高维空间（N维空间）压缩为低维空间（3维空间）。只需要找到 3xN的矩阵，要保证映射不同的点上，保持高维空间里面的度量信息。这个过程就是 present 过程，学习到高维空间降到低维空间的表示。

深度学习：原来要训练的专门的特征提取器，在深度学习直接用最简单的特征（例如：图片——像素值变成张量、语音——波形序列变成张量）。然后再设置额外的层，提取特征。整个过程是一起训练的 End2End。

基于规则和表征学习的区别

基于规则：人工设定，改进一些常见的算法。
表征学习：从数据进行训练得到算法的过程。

机器学习的算法选择流程图

机器学习的算法选择流程图，也被称作 scikit-learn 的算法作弊表（cheat sheet）。它为使用 scikit-learn 库的用户提供了一个决策树，帮助他们选择适合特定问题的机器学习算法。流程图按照不同的任务类型将算法分类为四个主要部分：

• 分类（Classification）: 用于预测离散的标签。
  • 流程开始于是否拥有超过50个样本，这是为了确认是否有足够的数据来训练模型。
  • 然后基于数据是文本型还是非文本型，是否有100k个样本等条件，指导选择合适的分类器，例如朴素贝叶斯（Naive Bayes）、支持向量机（SVM）、K近邻（KNeighbors）等。
• 回归（Regression）: 用于预测连续的值。
  • 同样首先判断样本数量。
  • 根据数据的特征数量和是否重要，选择适当的回归模型，如线性回归（LinearRegression）、岭回归（RidgeRegression）、随机梯度下降回归器（SGDRegressor）等。
• 聚类（Clustering）: 用于数据的群体划分，没有预先定义的标签。
  • 首先考虑样本的数量，以及是否知道要划分的类别数量。
  • 根据这些条件，建议使用不同的聚类算法，如 K-均值（KMeans）、谱聚类（SpectralClustering）、均值漂移（MeanShift）等。
• 降维（Dimensionality Reduction）: 当数据有很多特征时，用于降低特征的数量，同时尽可能保留原始数据的信息。
  • 根据样本数量和是否需要降低数据的结构复杂度，选择不同的降维技术，例如 PCA（主成分分析）、Isomap、LLE（局部线性嵌入）等。

流程图中每个算法旁边的注释提供了额外的选择信息，比如算法是否支持大规模数据集（noted by “scalable”）或者是否需要知道分类的数量（“number of categories known”）。这张流程图是新手和有经验的机器学习实践者快速参考的实用工具。

SVM的限制

视觉系统崛起

寒武纪，视觉系统，感知光的明暗，运动需求，趋光性，避光性，在物种进化保持优势**

人工神经网络：仿生学构建神经网络

让神经网络工作起来的算法：反向传播 Back Propagation

主要就是求导数。核心：计算图。

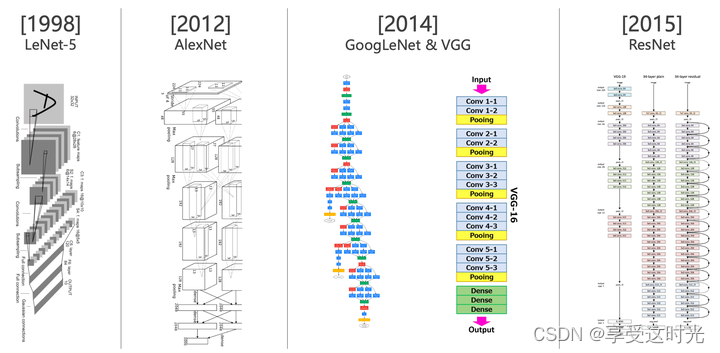
卷积神经网络历史

Machine Learning

2. 线性模型（Linear Model）

问题如下：

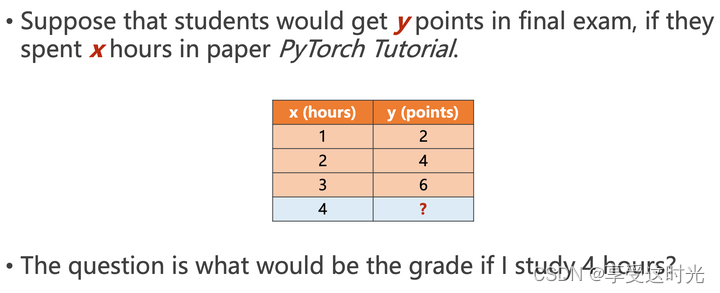
把已知数据作为训练集，要预测的数据集作为测试集。

但是这样会导致在训练集上过拟合，例如训练提供的是美颜后的猫，而测试集是一个一部分的猫头，可能就无法识别出来了。为了防止这种过拟合，必须把训练集划分一部分来做开发集（验证集）。

过拟合：

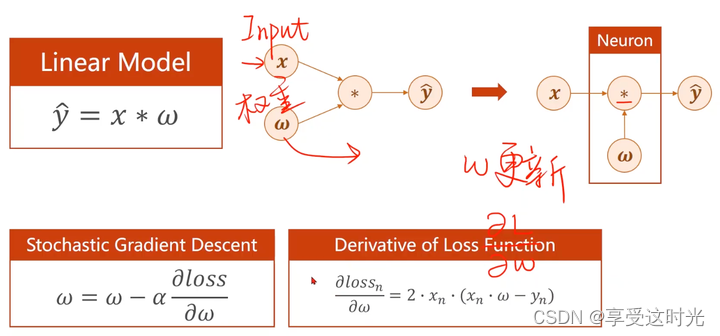
首先，这个问题，可以采用线性模型解决。设置模型为 y = x * w

随机选择 w，那怎么知道哪个 w 是正确的呢？或者最接近答案的呢？
采用 loss

w=0的损失如下

w=2的损失如下

loss

穷举法（计算量大）

搜索让loss最小的参数值

P1 作业代码

有w，b两个参数，穷举最小值：

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

x_data = [1.0, 2.0, 3.0]
y_data = [3.0, 4.0, 6.0]

def forward(x, w, b):
    return x * w + b

def loss(x, y, w, b):
    y_pred = forward(x, w, b)
    loss = (y_pred - y) ** 2
    return loss

w_list = np.arange(0.0, 4.1, 0.1)
b_list = np.arange(-2.0, 2.1, 0.1)

# mse_matrix用于存储不同 w,b 组合下的均方误差损失
mse_matrix = np.zeros((len(w_list), len(b_list)))

for i, w in enumerate(w_list):
    for j, b in enumerate(b_list):
        l_sum = 0
        for x_val, y_val in zip(x_data, y_data):
            l_sum += loss(x_val, y_val, w, b)
        mse_matrix[i, j]= l_sum/len(x_data)
W, B = np.meshgrid(w_list, b_list)
fig = plt.figure('Linear Model Cost Value')
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(W, B, mse_matrix.T, cmap='viridis')
ax.set_xlabel('w')
ax.set_ylabel('b')
ax.set_zlabel('loss')
plt.show()

但是，假设一个参数 w 就搜索了100个结果，搜索空间还可以，但是，如果是两个参数 w1，w2呢？就搜索空间就变成变成100的平方了。10个参数就 $100^{10}$。

因此穷举法，找到最优点，很不合理。

分治法（局部最优解）

分成4份，找16个点。然后最小值在绿色框里面，再在绿色框找4个点

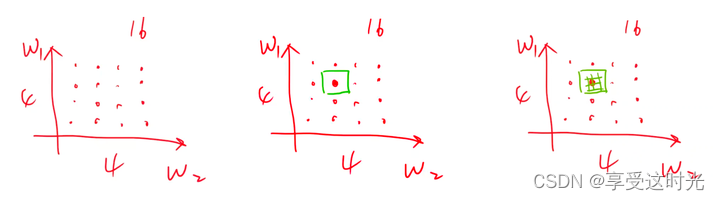
但是如果 cost function不是光滑的呢，不只有一个最小值呢？就会一直在一个地方搜索。不是最优值。

3. 梯度下降法（Gradient Descent）

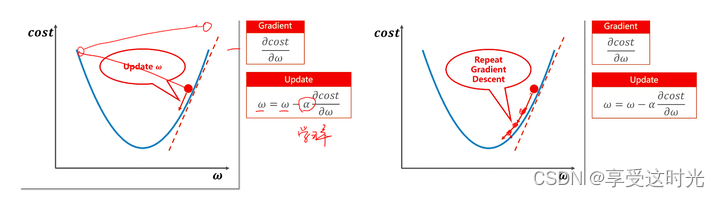
梯度下降法

为什么是梯度下降呢？

• 如果导数>0，相当于 x+Δx 后函数值变大了，即 f(x+Δx) - f(x) > 0（因为Δx>0，只有f(x+Δx) - f(x) > 0，导数才会大于0），说明是个增函数。说明往梯度的正方向就是向右，函数是在上升的。所以要往导数的负方向走，往左走。才能到最低点。
• 如果导数<0，说明随着 x 增加，函数值在减少，即 f(x+Δx) - f(x) < 0（因为Δx>0，只有f(x+Δx) - f(x) < 0，导数才会小于0），说明是个减函数。往回走函数是在上升的。

所以如果要下降，就得取导数的负方向。负的导数的方向就是最小值的方向。
梯度下降算法其实也算是贪心算法，因此找到的是局部最优点。那为什么深度学习还是普遍用梯度下降法呢？因为深度学习很少有局部最优点。

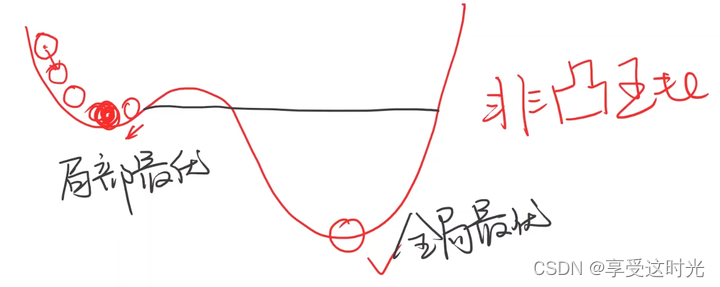
但是深度学习存在鞍点，梯度为0，使用梯度下降法可能无法走出鞍点。怎么解决在后续介绍

梯度下降法的具体计算

代码：梯度下降法

import numpy as np
import matplotlib.pyplot as plt

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

w = 1.0
learning_rate = 0.01

def forward(x, w):
    return x * w

def cost_fuction(xs, ys, w):
    cost = 0
    for x, y in zip(xs, ys):
        y_pred = forward(x, w)
        cost += (y_pred - y) ** 2
    return cost / len(xs)

def gradient(xs, ys, w):
    grad = 0
    for x, y in zip(xs, ys):
        grad += 2 * x * (x * w - y)
    return grad / len(xs)

print('predict (before training)', 4, forward(4, w))

epoch_list = []
cost_val_list = []

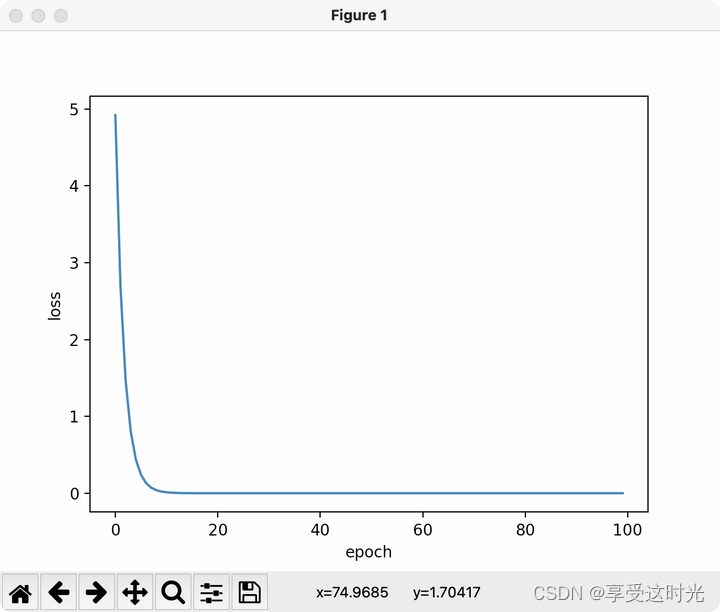
for epoch in range(100):
    cost_val = cost_fuction(x_data, y_data, w)
    grad_val = gradient(x_data, y_data, w)
    w -= learning_rate * grad_val
    print('Epoch: ', epoch, 'w=', w, 'loss=', cost_val)
    epoch_list.append(epoch)
    cost_val_list.append(cost_val)
print('predict (after training)', 4, forward(4, w))

plt.plot(epoch_list, cost_val_list)
plt.xlabel('epoch')
plt.ylabel('cost val')
plt.show()

有些时候下降不平滑，采样指数加权均值方法。使得 loss 更加的平滑

随机梯度下降（Stochastic Gradient Descent）

不拿整个cost function算，而是随机的一个loss。

因为遇到鞍点的时候，如果还是所有的cost来算，就出不来鞍点。而随机，就可能可以突破鞍点。相当于不走最优解的方向。

cost function 和 loss function算梯度的区别

（梯度下降和随机梯度下降）：
首先，如果是 全局梯度下降容易到鞍点出不来，所以需要采样随机梯度下降去突破。
但是随机的话，导致无法并行，时间复杂度太高，因为当前的 w 必须由上一个 w 来算。

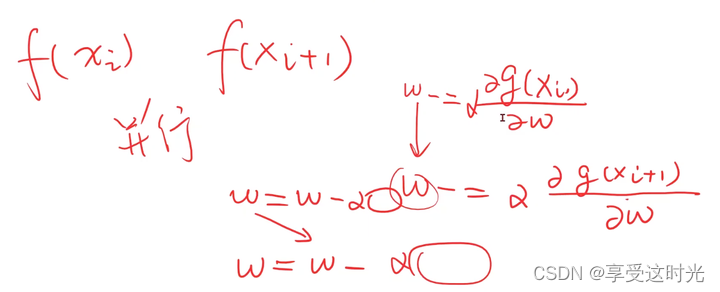
性能和时间对比

• 随机梯度下降可以找到最优点，不会在鞍点就停止。但是每个样本就会更新一次权重。时间复杂度太高了。
• 梯度下降使用整个数据集去，并行算法很快。虽然时间复杂度低，但是可能找到的不是最优点，是鞍点。
  全部仍在一起，性能不好，全部分开，时间复杂度不好，因此，折中，那就采用 mini-batch，批量的随机梯度下降。
  

代码：随机梯度下降

import matplotlib.pyplot as plt

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

w = 1.0
learning_rate = 0.01

def forward(x, w):
    return x * w

def loss(x, y, w):
    y_pred = forward(x, w)
    loss = (y - y_pred) ** 2
    return loss

def gradient(x, y, w):
    return 2 * x * (x * w - y)

print('predict (before training)', 4, forward(4, w))

epoch_list = []
loss_list = []

for epoch in range(100):
    for x, y in zip(x_data, y_data):
        # 拿到一个样本就更新了
        grad = gradient(x, y, w)
        w = w - learning_rate * grad
        print('\tgrad: ', x, y, grad)
        l = loss(x, y, w)
    print('process: ', epoch, "w=", w, 'loss=', l)
    epoch_list.append(epoch)
    loss_list.append(l)
print('predict (after training)', 4, forward(4, w))

plt.plot(epoch_list, loss_list)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()

4. 反向传播（Backward）

简单模型（loss的梯度容易算）

复杂模型（loss梯度怎么算）

层数多了，化简后还是线性函数

需要加入非线性函数使得它没办法化简

前向传播和反向传播

例子：
前馈：通向下一步运算的输出值 + 局部梯度

代码流程思路

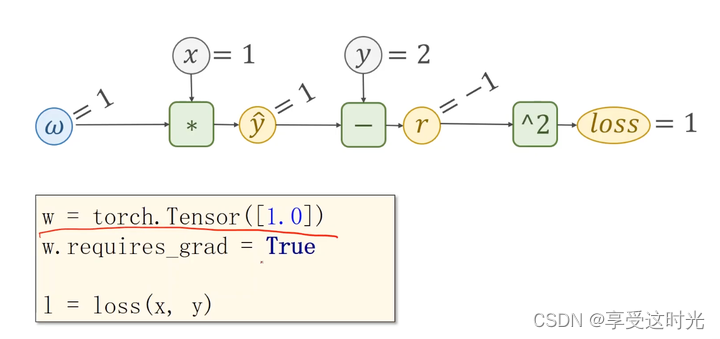
Tensor 保存 data和 grad

构建数据
注意要使用 Tensor，并且打开 requires_grad

创建模型
forward

loss：其实本质就是构建一个计算图
在写代码的时候要注意能够把这个图画出来

训练过程
前馈过程，只需要计算 loss 就好了。

反向传播

loss算出来是一个张量，调用它的成员函数 backward()，自动把这条计算链路上所有需要梯度的地方都给求出来。求出来后都存在变量里面。存完之后，计算图就释放了，就没有了。下一次再进行loss计算的时候，再创建一个新的计算图。

为什么要 w.grad.data ？ 因为 grad 也是一个 tensor，如果不取到 data，就会产生计算图，就会对w的权重又进行修改。我们并不希望我在修改数值的过程导致了权重的变化。而取到data到话，是不会建立计算图的。

注意：如果要算所有样本的平均 loss， sum += l，就完全了。一直在构建图，内存被吃光了。要用 sum += l.item()。

接下来，梯度清0

总结：整个过程

1. 数据，梯度更新，loss构建了计算图

2. 然后 l.backward()，自动算梯度

代码：反向传播

# 如果是复杂的网络，没办法都自己写gradient的计算。
import torch
import matplotlib.pyplot as plt

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

w = torch.Tensor([1.0])
w.requires_grad = True

def forward(x, w):
    return x * w

def loss(x, y, w):
    y_pred = forward(x, w)
    loss = (y - y_pred) ** 2
    return loss

print('predict (before training)', 4, forward(4, w.item()))

epoch_list = []
loss_list = []

for epoch in range(100):
    for x, y in zip(x_data, y_data):
        l = loss(x, y, w)
        l.backward()
        print('\tgrad:', x, y, w.grad.item())
        w.data = w.data - 0.01 * w.grad.data
        w.grad.data.zero_()
    print('process:', epoch, l.item())
    epoch_list.append(epoch)
    loss_list.append(l.item())

print('predict (after training)', 4, forward(4, w))

plt.plot(epoch_list, loss_list)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()

5. 用 Pytorch 实现线性回归

1. 准备数据：向量化

补充知识：pytorch的广播机制

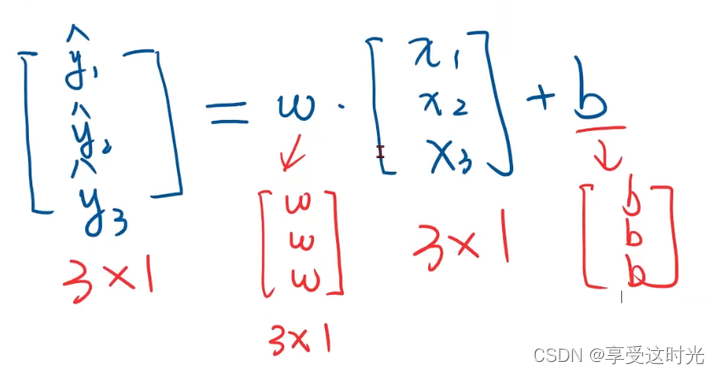
loss：最后是矩阵表示，一般最后会均值或者sum，变成标量。

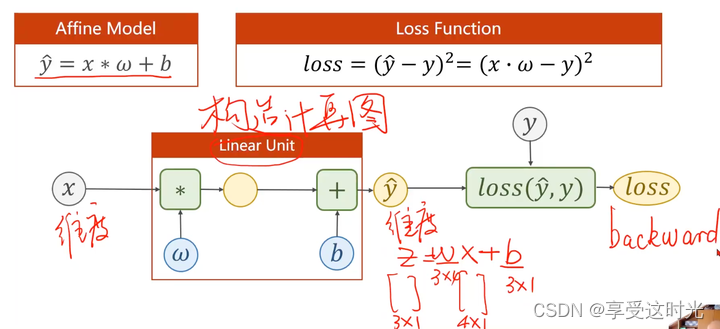
2. 设计模型（torch.nn.Module）

之前的做法：人工计算梯度，现在直接调用pytoch

在pytorch里面，我们不再考虑人工求导数了，重点目标：构造计算图。
要确定 w, b 的大小

模版：torch.nn.Module，深度学习后面的函数也都是这样定义的

注意：最少实现两个函数，init() 构造函数， forward()前馈。
torch.nn.Module 自动实现了 backward()函数了。

为什么可以直接 self.linear(x)？

• 因为函数实现了 def call(self, *args, **kwargs)函数
• pytorch 的 torch.nn.Module 里面的 call 函数里面，有一个关键的函数就是调用了 forward（self, ）函数，输入x，然后实现 wx+b的计算。
• 所以我们写的forward本质上是覆盖掉，也就是重写（overwrite）了torch.nn.Module 的forward函数，去实现我们自己的前馈。
• 执行model() 会自动调用 LinearModel 的__call__ 然后__call__又会调用 实现的forward()

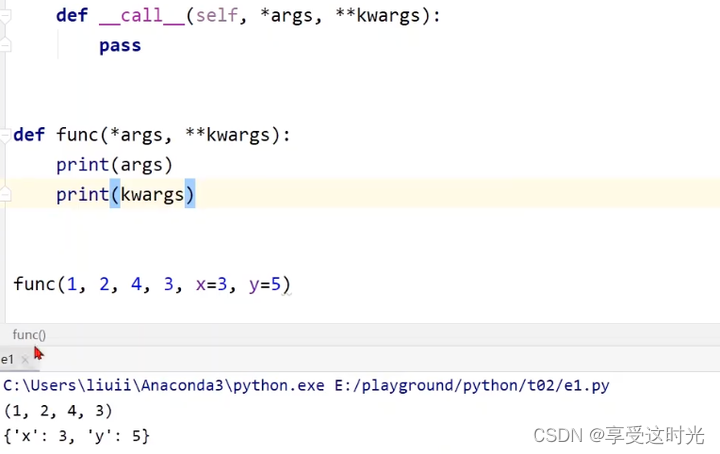
补充知识：*args 和 **kwargs分别是什么？

• *args：没有给名字的参数
• **kwargs：给名字的参数

将来要用模型就实例化模型就好了 model = LinearModel()

3. 构造 loss 和 optimizer

loss 计算过程，也要构建计算图，只要要构建计算图，就要继承 nn.Module

optimizer

model.parameters会检查所有成员，如果成员里面有权重，就都加到最后训练的参数集合上。

递归的方式，把全部的参数找出来。

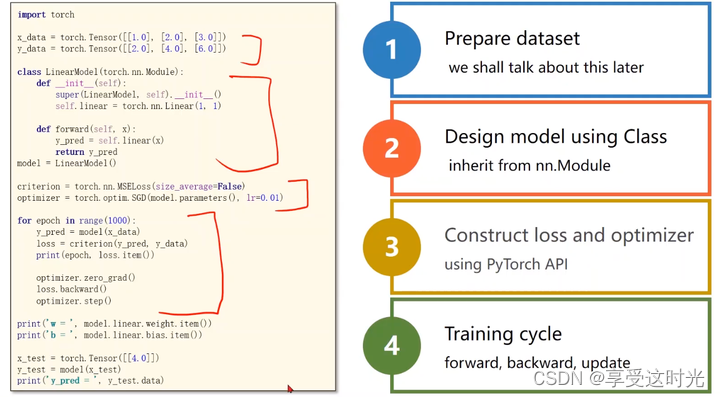
4. 训练过程（五步）

Forward：Predict	model(x_data)	y_hat
Forward：Loss	criterion(y_pred, y_data)	loss
set the grad to zero!!!	optimizer.zero_gard()	grad zero
Backward：Autograd	loss.backward()	backward
Update	optimizer.step()	update

为什么要item呢？因为weight的结果可能是矩阵[[]], item是把里面的值拿出来。而不是打印矩阵

P5 作业：使用不同的优化器

import torch
import matplotlib.pyplot as plt

# step 1: Prepare Dataset
x_data = torch.Tensor([[1.0], [2.0], [3.0]])
y_data = torch.Tensor([[2.0], [4.0], [6.0]])

# step 2: Design Model
class LinearModel(torch.nn.Module):
    def __init__(self):
        super(LinearModel, self).__init__()
        self.linear = torch.nn.Linear(1, 1, bias=True)
    def forward(self, x):
        y_pred = self.linear(x)
        return y_pred
models = {
    'SGD': LinearModel(),
    'Adam': LinearModel(),
    'Adagrad': LinearModel(),
    'Adamax': LinearModel(),
    'ASGD': LinearModel(),
    'RMSprop': LinearModel(),
    'Rprop': LinearModel(),
}

# step 3: Donstruct Loss and Optimizer
criterion = torch.nn.MSELoss(size_average=False)
optimizer = {
    'SGD': torch.optim.SGD(models['SGD'].parameters(), lr=0.01),
    'Adam': torch.optim.Adam(models['Adam'].parameters(), lr=0.01),
    'Adagrad': torch.optim.Adagrad(models['Adagrad'].parameters(), lr=0.01),
    'Adamax': torch.optim.Adamax(models['Adamax'].parameters(), lr=0.01),
    'ASGD': torch.optim.ASGD(models['ASGD'].parameters(), lr=0.01),
    'RMSprop': torch.optim.RMSprop(models['RMSprop'].parameters(), lr=0.01),
    'Rprop': torch.optim.Rprop(models['RMSprop'].parameters(), lr=0.01),
    }

loss_values = {k: [] for k in optimizer.keys()}

# step 4: Training Cycle
for opt_name, optimizer in optimizer.items():
    model = models[opt_name]
    for epoch in range(100):
        y_pred = model(x_data)              # forward predict
        loss = criterion(y_pred, y_data)    # forward loss
        optimizer.zero_grad()               # set the grad to zero
        loss.backward()                     # backward
        optimizer.step()                    # update

        loss_values[opt_name].append(loss.item())

plt.figure(figsize=(10, 5))
for opt_name, losses in loss_values.items():
    plt.plot(losses, label=opt_name)

plt.xlabel("Epoch")
plt.ylabel("Loss")
plt.legend()
plt.title("Loss by Optimization Algorithm")
plt.show()

6. logistics 回归（但是做的是分类任务）

线性回归：y是一个连续的值

分类问题的定义

但是如果用回归做分类问题，例如：

• 如果第0个类别，就让y输出为0，
• 如果是第一个类别，就让y输出为1。

这种思路是不好的，因为在构建类别编号的时候，0和1挨着，0和9差别就很大。

但是如下图，789。7和9输入特征空间里面近似，但是输出结果中间却隔了个8，这个输出说明7和8的输出值更接近。但是7和8在输入空间上差别的比较远。这是不对的，因为我们只是做类别的比较，而两种图片之间是否存在某种大小关系是没办法建立这样的一个直觉上的思维。

因此，我们去估算这个结果的时候，不再估算输出的值，而是根据输入x，输出为不同类别的概率为多少。概率值加起来应该等于1。

分类任务是离散的。类别之间没有数值大小的含义。

常见分类数据集

MNIST数据集

CIFAR-10

二分类问题

回归任务，表示将来能拿到的点数 ——> 变成能否通过考试，fail 和 pass，二分类

想要输出为概率，因此需要 logistic function，把实数的值映射到0-1。

注意：并不是 logistic 函数就能进行概率的转换，而是，我们想要计算概率，必须保证我们的输出在0～1之间。

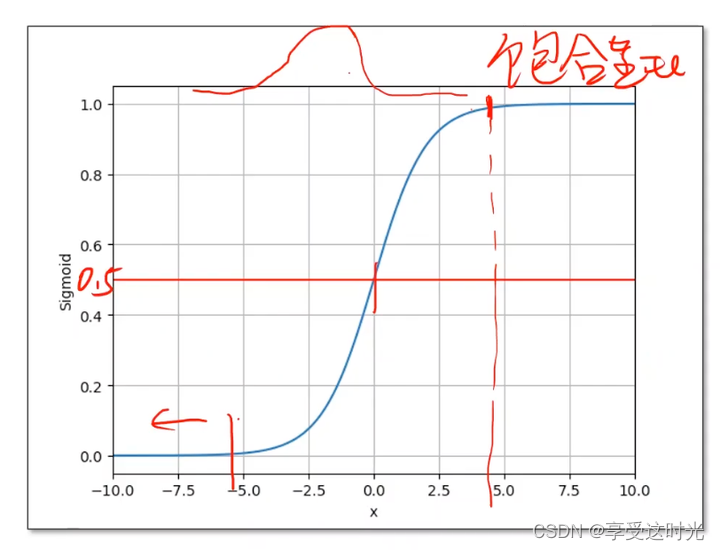
sigmoid functions

model 区别

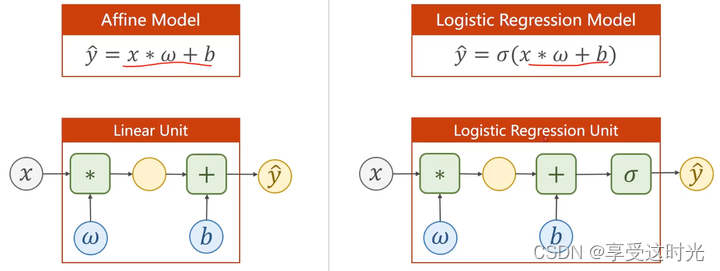
loss区别

loss变成分布，计算两个分布的相似度

计算相似度的方法：KL散度 和 cross-entropys

因此，二分类问题的loss选择的是二分类交叉熵

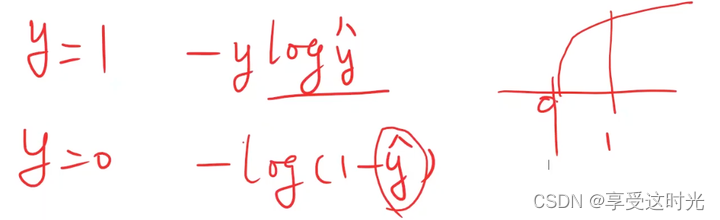
y=1, 观察loss函数，yhat越接近1，loss越小，并且离y值也越近。y=0的时候同理。

分类问题与回归问题代码区别

forward：加了个 sigmoid，把输出映射到0～1

均值可以求也可以不求，主要影响学习率的设置，导数会有 1/N。

P6 作业：使用不同的优化器

代码：Logistic回归

import torch
import torch.nn.functional as F
import matplotlib.pyplot as plt

x_data = torch.Tensor([[1.0], [2.0], [3.0]])
y_data = torch.Tensor([[0], [0], [1]])

class Logistic_Regression_Model(torch.nn.Module):
    def __init__(self):
        super(Logistic_Regression_Model, self).__init__()
        self.linear = torch.nn.Linear(1, 1, bias=True)

    def forward(self, x):
        y_pred = F.sigmoid(self.linear(x))
        return y_pred
    
models = {
    'SGD': Logistic_Regression_Model(),
    'Adam': Logistic_Regression_Model(),
    'Adagrad': Logistic_Regression_Model(),
    'Adamax': Logistic_Regression_Model(),
    'ASGD': Logistic_Regression_Model(),
    'RMSprop': Logistic_Regression_Model(),
    'Rprop': Logistic_Regression_Model(),
}

criterion = torch.nn.BCELoss(size_average=False)
optimizers = {
    'SGD': torch.optim.SGD(models['SGD'].parameters(), lr=0.01),
    'Adam': torch.optim.Adam(models['Adam'].parameters(), lr=0.01),
    'Adagrad': torch.optim.Adagrad(models['Adagrad'].parameters(), lr=0.01),
    'Adamax': torch.optim.Adamax(models['Adamax'].parameters(), lr=0.01),
    'ASGD': torch.optim.ASGD(models['ASGD'].parameters(), lr=0.01),
    'RMSprop': torch.optim.RMSprop(models['RMSprop'].parameters(), lr=0.01),
    'Rprop': torch.optim.Rprop(models['RMSprop'].parameters(), lr=0.01),
    }

loss_values = {k: [] for k in optimizers.keys()}

for opt_name, optimizer in optimizers.items():
    model = models[opt_name]
    for epoch in range(1000):
        y_pred = model(x_data)
        loss = criterion(y_pred, y_data)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

        loss_values[opt_name].append(loss.item())

plt.figure(figsize=(10, 5))

for opt_name, losses in loss_values.items():
    plt.plot(losses, label=opt_name)

plt.xlabel('Epoch')
plt.ylabel("Loss")
plt.legend()
plt.title("Loss by Optimization Algorithm")
plt.show()

7. 处理多维度特征

输入存在多个特征

一个特征，变成多个特征。一个特征对应一个 w 参数。

mini-batch情况

上标是样本数，下标是特征

为什么要转换成矩阵运算？可以利用并行计算的能力，提高整个运算的速度

矩阵降维

那如果输入是8维，输出是2维呢？但是我们要的是一维的输出呀？
没关系，再接一个 torch.nn.Linear(2,1)就好了呀。

补充：什么是矩阵？

矩阵是一个空间转换的函数。

但是一定要加 sigmoid（深度学习成为激活函数）。不然化简之后都是线性变换。

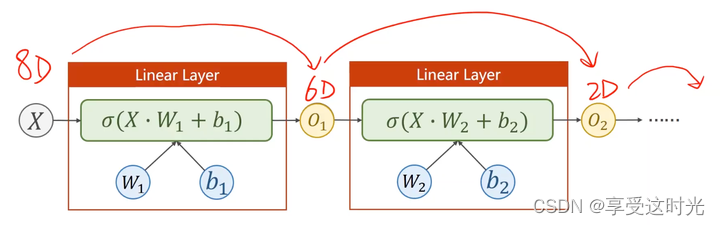
直接8维降1维中间的神经元少，学习效果可能不佳，所以要多几层，但是也不能太多，否则会造成过拟合。

P7 作业：使用不同的激活函数

import torch
import numpy as np
import matplotlib.pyplot as plt

# 读取压缩包 np.loadtxt， delimier：分隔符
xy = np.loadtxt('PyTorch深度学习实践/diabetes.csv.gz', delimiter=',', dtype=np.float32)
x_data = torch.from_numpy(xy[:, :-1])
y_data = torch.from_numpy(xy[:, [-1]])

class Model(torch.nn.Module):
    def __init__(self, activation_fn=torch.nn.Sigmoid()):
        super(Model, self).__init__()
        self.linear1 = torch.nn.Linear(8, 6)
        self.linear2 = torch.nn.Linear(6, 4)
        self.linear3 = torch.nn.Linear(4, 1)
        self.activation_fn = activation_fn
    def forward(self, x):
        x = self.activation_fn(self.linear1(x))
        x = self.activation_fn(self.linear2(x))
        x = torch.sigmoid(self.linear3(x))
        return x

activation_fns = {
    'Sigmoid': torch.nn.Sigmoid(),
    'ReLU': torch.nn.ReLU(),
    'Tanh': torch.nn.Tanh(),
    'Softplus': torch.nn.Softplus(),
}

criterion = torch.nn.BCELoss(reduction='mean')

loss_values = {k: [] for k in activation_fns.keys()}

for activation_name, activation_fn in activation_fns.items():
    model = Model(activation_fn=activation_fn)
    optimizer = torch.optim.SGD(model.parameters(), lr=0.1)

    for epoch in range(100):
        y_pred = model(x_data)
        loss = criterion(y_pred, y_data)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        
        loss_values[activation_name].append(loss.item())

plt.figure(figsize=(10, 5))

for activation_name, losses in loss_values.items():
    plt.plot(losses, label=activation_name)

plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.title('Loss by Sigmoid Algorithm')
plt.legend()
plt.show()

8. 加载数据集

• 随机梯度下降：如果只是用一个样本，将来会得到一个比较好的随机性，可以跨越在优化中遇到的鞍点，训练出来的模型性能会更好。但是优化时间过长，每次就一个样本没法利用 CPU 和 GPU 的并行能力进行加速。
• Batch：最大化的利用向量计算的优势，提升计算速度。但是性能不是最优的，可能陷入鞍点。

所以采用 Mini-Batch 来均衡时间和性能上平衡的需求。

Epoch，Batch-Size，Iterations 概念

• Epoch: One forward pass and one backward pass of all the training examples. （遍历完一整个数据集）
• Batch-Size: The number of training examples in one forward backward pass. （每次训练的时候所用的样本数量）
• Iterations：Number of passes, each pass using [batch size] number of examples.

假设有10000个样本，Batch-Size=1000，Iterations = 10000/1000=10

Dataset & Dataloader

Dataloader：能够划分batch_size，也要能够随机打乱。具体后面介绍参数。

注意：torch里面的Dataset 是一个抽象类，不能实例化

补充知识：魔法函数（getitem，len）

getitem：实例化类后，可以下标操作

len：返回数据数量

构造数据集的时候，init的两种选择

1. init：把所有数据，都在 init 加载进来，都在内存里面，然后每次使用 getitem的时候，把构造好的数据集的第 i 个样本传出来就好了。适合本身数据集容量不大的情况。
2. 如果读取的数据集是图像数据集，如果10几个g，全部加载肯定不太可能。所以init只是做一些初始化，或者定义一个读写文件，例如列表，用来放每个数据的文件名。然后getitem的时候读取列表的第 i 个元素的文件名，再去加载文件的内容。
   

Dataloader

• dataset：传递数据集对象
• batch_size：小批量的数量
• shuffle：是否打乱数据
• num_worker：读数据的时候，读取构成 mini_batch 的时候，是否要多线程，是否要并行，要几个并行进程读取数据。取决于 gpu 的核心。
  

代码实现关键

主要部分是 data 数据解耦 为 x 和 y

torchvision里面的数据集

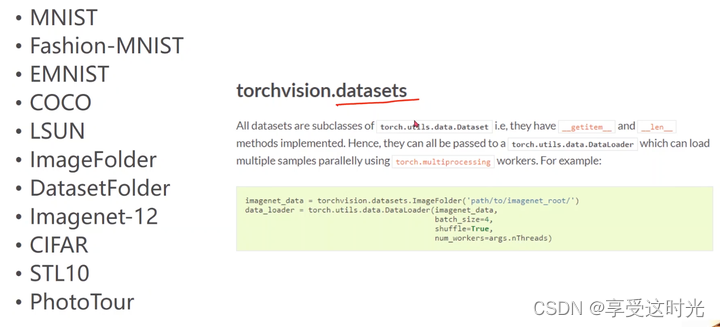
代码：Dataloader

import torch
import numpy as np
from torch.utils.data import Dataset
from torch.utils.data import DataLoader
from torch.utils.data import random_split
import matplotlib.pyplot as plt

class Diabetes_Dataset(Dataset):
    def __init__(self, filepath):
        super(Diabetes_Dataset, self).__init__()

        # 读取数据
        xy = np.loadtxt(filepath, delimiter=',', dtype=np.float32)
        self.len = xy.shape[0]
        self.x_data = torch.from_numpy(xy[:, :-1])
        self.y_data = torch.from_numpy(xy[:, [-1]])
    
    def __getitem__(self, index):
        return self.x_data[index], self.y_data[index]
    
    def __len__(self):
        return self.len
    
class Logistic_Model(torch.nn.Module):
    def __init__(self):
        super(Logistic_Model, self).__init__()
        self.linear1 = torch.nn.Linear(8, 6)
        self.linear2 = torch.nn.Linear(6, 4)
        self.linear3 = torch.nn.Linear(4, 1)
        self.activate = torch.nn.ReLU()
        
    def forward(self, x):
        x = self.activate(self.linear1(x))
        x = self.activate(self.linear2(x))
        x = torch.sigmoid(self.linear3(x))
        return x
    
# 加载数据集并划分为训练集和测试集
dataset = Diabetes_Dataset('PyTorch深度学习实践/diabetes.csv.gz')
train_size = int(len(dataset) * 0.8)
test_size = len(dataset) - train_size
train_dataset, test_dataset = random_split(dataset, [train_size, test_size])

train_loader = DataLoader(dataset=train_dataset, batch_size=32, shuffle=True, num_workers=2)
test_loader = DataLoader(dataset=test_dataset, batch_size=32, shuffle=False, num_workers=2)

# 初始化模型、损失函数和优化器
model = Logistic_Model()
criterion = torch.nn.BCELoss(reduction='mean')
optimizer = torch.optim.SGD(model.parameters(), momentum=0.1, weight_decay=0.9, lr=0.01)

# 训练模型
epoch_list = []
loss_list = []
for epoch in range(100):
    total_loss = 0.0
    for i, data in enumerate(train_loader):
        inputs, labels = data
        y_pred = model(inputs)
        loss = criterion(y_pred, labels)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        total_loss += loss.item()

    average_loss = total_loss / len(train_loader)
    epoch_list.append(epoch)
    loss_list.append(average_loss)
    print("Epoch:", epoch, "average loss:", average_loss)

# 可视化训练过程
plt.figure(figsize=(10, 5))
plt.plot(epoch_list, loss_list)
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.title('Dataset & Dataloader')
plt.show()

# 测试模型
model.eval()
correct = 0
total = 0

with torch.no_grad():
    for inputs, labels in test_loader:
        outputs = model(inputs)
        predicted = (outputs > 0.5).float()  # 将输出概率转换为0或1
        total += labels.size(0)
        correct += (predicted == labels).sum().item()

accuracy = 100 * correct / total
print(f'Accuracy: {accuracy:.2f}%')

P8 作业：Kaggle Titanic

数据下载地址：https://www.kaggle.com/c/titanic/data

当评估泰坦尼克号数据集中的特征与生还可能性的关联时，我们可以基于历史资料、统计学习和领域知识来进行一些推测：

1. Pclass（乘客等级）: 社会经济地位是一个重要因素，高等级乘客（如1等舱）可能有更高的生还几率。
2. Name（名字）: 虽然名字本身可能与生还率无关，但可以从名字中提取称谓（如 Mr., Mrs., Miss.），这可能反映了性别、婚姻状况和社会地位。
3. Sex（性别）: 历史记录显示，女性和儿童在灾难中的生还率更高，因为他们通常会被优先疏散。
4. Age（年龄）: 同样，儿童和年轻人可能有更高的生还几率。
5. SibSp（兄弟姐妹/配偶数量）和 Parch（父母/子女数量）: 这些特征反映了家庭结构，家庭成员可能会互相帮助，影响生还率。然而，太大的家庭可能在疏散时遇到困难。
6. Ticket（船票信息）: 船票信息可能隐含着有用的信息，比如团体旅行或位置信息，但这需要更深入的分析来决定其相关性。
7. Fare（票价）: 票价可能与 Pclass 相关，较高的票价可能意味着更高的社会经济地位和更高的生还几率。
8. Cabin（船舱号）: 船舱号可能与船上的位置有关，一些位置在船沉时可能更安全或者更容易疏散。
9. Embarked（登船口）: 登船口可能是一个次要因素，但如果某些登船口的乘客普遍属于特定的社会经济群体，这可能会间接影响生还率。

import pandas as pd
import torch
import torch.nn.functional as F
from torch.utils.data import Dataset, DataLoader
from sklearn.preprocessing import LabelEncoder, StandardScaler
import matplotlib.pyplot as plt

# 自定义 PyTorch 数据集类，用于加载和预处理 Titanic 数据集
# 数据下载地址：https://www.kaggle.com/c/titanic/data
class TitanicDataset(Dataset):
    def __init__(self, filepath, scaler=None, is_train=True):
        super(TitanicDataset, self).__init__()

        # 初始化函数，读取 CSV 文件
        self.dataframe = pd.read_csv(filepath)
        self.scaler = scaler
        # 调用预处理函数来处理 DataFrame
        self.preprocess(self.dataframe, is_train)

    def preprocess(self, df, is_train):
        # 移除不需要的类别
        df.drop(['PassengerId', 'Name', 'Ticket', 'Cabin'], axis=1, inplace=True)
        
        # 处理缺失值
        df['Age'].fillna(df['Age'].mean(), inplace=True)                # Age 缺失的值用平均值来填充
        df['Fare'].fillna(df['Fare'].mean(), inplace=True)              # Fare 缺失的值用平均值来填充
        df['Embarked'].fillna(df['Embarked'].mode()[0], inplace=True)   # Embarked 缺失的值用众值来填充

        # 使用 LabelEncoder 来转换性别和登船口为数值形式
        # LabelEncoder 适用于将文本标签转换为一个范围从 0 到 n_classes-1 的数值。这种方法适用于转换具有顺序性的分类特征。例如“低”，“中”，“高”。
        label_encoder = LabelEncoder()
        df['Sex'] = label_encoder.fit_transform(df['Sex'])
        df['Embarked'] = label_encoder.fit_transform(df['Embarked'])

        # 与 LabelEncoder 不同，One-Hot 编码 创建了一个二进制列来表示每个类别，没有数值的大小意义。当分类特征的不同类别之间没有顺序或等级的概念时，通常使用独热编码。
        # 注意：要使用 One-Hot的话，input_features=10
        # df = pd.get_dummies(df, columns=['Sex', 'Embarked'])

        if is_train:
            # 如果是训练集，创建新的 StandardScaler，并进行 fit_transform, 来标准化 'Age' 和 'Fare' 列的数值
            # 如果特征的数值范围差异很大，那么算法可能会因为较大范围的特征而受到偏向，导致模型性能不佳。
            self.scaler = StandardScaler()
            df[['Age', 'Fare']] = self.scaler.fit_transform(df[['Age', 'Fare']])

            # 如果是训练数据，将 'Survived' 列作为标签
            self.labels = df['Survived'].values
            self.features = df.drop('Survived', axis=1).values

        else:
            # 如果是测试集，使用传入的 scaler 进行 transform
            df[['Age', 'Fare']] = self.scaler.transform(df[['Age', 'Fare']])

            # 对于测试数据，可能没有 'Survived' 列，因此特征就是整个 DataFrame
            self.features = df.values
            self.labels = None      # 标签设置为 None


    def __len__(self):
        return len(self.dataframe)

    def __getitem__(self, index):
        # 获取单个样本，包括特征和标签（如果有的话）
        # 如果有标签，同时返回特征和标签
        if self.labels is not None:
            return torch.tensor(self.features[index], dtype=torch.float), torch.tensor(self.labels[index], dtype=torch.float)
        # 对于没有标签的测试数据，返回一个占位符张量，例如大小为 1 的零张量
        else:
            return torch.tensor(self.features[index], dtype=torch.float), torch.zeros(1, dtype=torch.float)


# 自定义 二分类模型
class BinaryClassificationModel(torch.nn.Module):
    def __init__(self, input_features):
        super(BinaryClassificationModel, self).__init__()
        self.linear1 = torch.nn.Linear(input_features, 64)
        self.linear2 = torch.nn.Linear(64, 64)
        self.linear3 = torch.nn.Linear(64, 1)       

        # 定义 dropout 层，可以减少过拟合
        self.dropout = torch.nn.Dropout(p=0.1)

        # 定义 batchnorm层，帮助稳定学习过程
        self.batchnorm1 = torch.nn.BatchNorm1d(64)
        self.batchnorm2 = torch.nn.BatchNorm1d(64)
        
    def forward(self, x):
        x = F.relu(self.linear1(x))     # 第一层激活函数为 ReLU
        x = self.batchnorm1(x)          # 应用 batch normalization
        x = self.dropout(x)             # 应用 dropout

        x = F.relu(self.linear2(x))     # 第二层激活函数为 ReLU
        x = self.batchnorm2(x)          # 应用 batch normalization
        x = self.dropout(x)             # 应用 dropout

        x = self.linear3(x)             # 输出层
        return torch.sigmoid(x)         # 应用 sigmoid 激活函数

# 训练过程
def train(models, train_loader, criterion, optimizers, num_epochs):
    epoch_losses = {k: [] for k in optimizers.keys()}

    print('start training')

    for optim_name, optimizer in optimizers.items():
        model = models[optim_name]
        for epoch in range(num_epochs):
            model.train()
            running_loss = 0.0
            for batch_idx, (inputs, labels) in enumerate(train_loader):
                optimizer.zero_grad()                       # 梯度清零
                outputs = model(inputs)                     # 前向传播
                loss = criterion(outputs.squeeze(), labels) # 使用 squeeze 调整输出形状
                loss.backward()                             # 反向传播
                optimizer.step()                            # 更新权重
                # 乘以 inputs.size(0) 的目的是为了累积整个批次的总损失，而不仅仅是单个数据点的平均损失。
                # 调用 loss = criterion(outputs, labels) 时，计算的是当前批次中所有样本的平均损失。
                # 为了得到整个训练集上的总损失，我们需要将每个批次的平均损失乘以该批次中的样本数（inputs.size(0)）。
                # 这样做可以确保每个样本，无论它们属于哪个批次，对总损失的贡献都是平等的。
                running_loss += loss.item() * inputs.size(0)
            epoch_loss = running_loss / len(train_loader.dataset)
            print(f'Epoch {epoch+1}/{num_epochs} Loss: {epoch_loss:.4f}')
            epoch_losses[optim_name].append(epoch_loss)
    return epoch_losses

# 测试
def test(model, test_loader, optimizers):
    results = {}
    for optim_name, _ in optimizers.items():
        model = models[optim_name]
        model.eval()
        
        predictions = []
        with torch.no_grad():   # 不计算梯度，减少计算和内存消耗
            for inputs, _ in test_loader:
                outputs = model(inputs)
                # test没有标签，只输出结果
                predicted = (outputs > 0.5).float().squeeze()
                predictions.extend(predicted.tolist())  # 使用 extend 和 tolist 将 predicted 中的每个元素添加到 predictions
        print("Predict result: ", predictions)
        results[optim_name] = predictions
    return  results

    #         # 如果是验证集，同时有标签，就可以算精度，但是我们的test没有标签
    #         # torch.max(outputs.data, 1): 这一行是在查找每个样本预测概率最高的类别。torch.max 返回两个结果：最大值和它们的索引。
    #         # 由于我们只关心最大概率的索引（即预测的类别），因此使用 _ 来忽略第一个返回值（最大概率值本身），而 predicted 保存了这些索引。
    #         # _, predicted = torch.max(output.data, 1)

    #         # 对于二分类问题，可以直接将 sigmoid 输出阈值化（例如，阈值 0.5）来获取预测标签。
    #         predicted = (outputs > 0.5).float().squeeze()
    #         total += labels.size(0)
    #         correct += (predicted == labels).sum().item()
    # accuracy = 100 * correct / total
    # print(f'Accuracy: {accuracy:.2f}%')


# 加载数据
# 训练数据集，没有传入 scaler，因此会创建一个新的
train_dataset = TitanicDataset('data/titanic/train.csv', scaler=None, is_train=True)
train_loader = DataLoader(dataset=train_dataset, batch_size=32, shuffle=True, num_workers=0)

# 测试数据集，传入从训练数据集得到的 scaler
test_dataset = TitanicDataset('data/titanic/test.csv', scaler=train_dataset.scaler, is_train=False)
test_loader = DataLoader(dataset=test_dataset, batch_size=32, shuffle=False, num_workers=0)

# 实例化模型，输入特征数量为10: Pclass Name Sex Age SibSp Parch Ticket Fare Cabin Embarked
# 但是注意，预处理之后，只采用了7个: Pclass Sex Age SibSp Parch Fare Embarked
models = {
    'Adam': BinaryClassificationModel(input_features=7),
    'SGD': BinaryClassificationModel(input_features=7),
    }

# 定义损失函数，优化器
criterion = torch.nn.BCELoss(reduction='mean')
optimizers = {
    'Adam': torch.optim.Adam(models['Adam'].parameters(), lr=0.001, betas=(0.9, 0.999), eps=1e-8, weight_decay=0.0001),
    'SGD': torch.optim.SGD(models['SGD'].parameters(), lr=0.01, weight_decay=0.001, momentum=0.9)
}


# 训练模型
num_epochs = 100
losses = train(models, train_loader, criterion, optimizers, num_epochs)

# 测试模型
# 已知test的结果保存在 gender_submission.csv 文件中，获取准确的 labels 和 predicted 结果算精度
labels_path = 'data/titanic/gender_submission.csv'
data_frame = pd.read_csv(labels_path)
data_frame.drop(['PassengerId'], axis=1, inplace=True)
labels = data_frame['Survived'].values
print('Test Dataset 正确结果: ', labels)

# 模型预测结果
results = test(models, test_loader, optimizers)
print('Test Dataset 预测结果: ', results)

# 精度计算
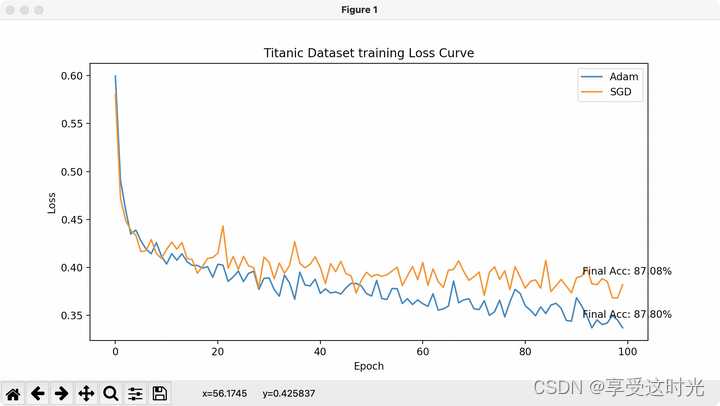
for optimizer_name, predicted in results.items():
    accuracy = 100 * (predicted == labels).sum() / len(predicted)
    print(f'Accuracy for {optimizer_name}: {accuracy:.2f}%')


plt.figure(figsize=(10, 5))
for optim_name, losses in losses.items():
    plt.plot(losses, label=optim_name)
    final_accuracy = 100 * (results[optim_name] == labels).sum() / len(results[optim_name])
    plt.annotate(f'Final Acc: {final_accuracy:.2f}%', xy=(num_epochs - 1, losses[-1]), xytext=(-40, 10), textcoords='offset points', fontsize=10)

plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.title('Titanic Dataset training Loss Curve')
plt.legend()
plt.show()

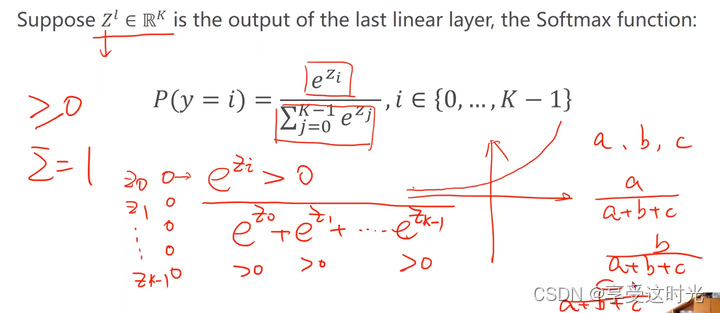
9. 多分类问题（Softmax Classifier）

二分类问题变成多分类

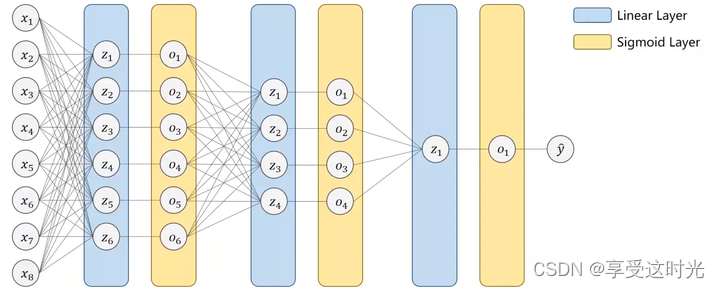
深度学习常见数据集，mnist，包含10个类别。那怎么运用 softmax把输出变成多分类任务呢？

怎么把二分类变成一个10分类？

二分类变成多分类的第一种方式

直接变成10个输出，输出每一个分类的概率，把每一个类别都看成一个二分类的问题。

但是这个输出结果是相互独立的。因为这个概率是针对某个类别做是否属于这类的二分类，没有考虑其他类别之间的依赖关系，所以概率看起来会有些怪。

而对于多分类任务来说，输出的结果之间应该是相互关联，相互抑制的。

• 它们的概率都要大于等于 0；
• 它们的和要等于1，满足离散分布的要求。

输出之间带有竞争性，如果 y=1的概率大， 其他的概率就得小。输出就是一个分布。

二分类变成多分类的第二种方式

增加一个softmax层

分子幂运算：保证所有输出结果 大于等于 0
分母求和：保证概率相加 = 1， $\frac{a}{a+b+c}+\frac{b}{a+b+c}+\frac{c}{a+b+c}=1$

补充知识：交叉熵

交叉熵损失（Cross-Entropy Loss）的计算公式是∑ylog(y_hat)，它用于衡量模型的预测值 y_hat 与真实目标值 y 之间的相似度。在分类任务的背景下，其中y 表示真实的类别标签，y_hat 表示模型预测的类别概率。

以下是关于交叉熵与相似度之间关系的解释，并提供一个例子：

• 较高的相似度： 如果模型的预测概率 y_hat 与真实的类别概率 y 非常相似，意味着模型对正确的类别有很高的置信度，那么交叉熵损失会较低。换句话说，较低的交叉熵表示模型性能较好，模型的预测结果与真实标签的相似度较高。
• 较低的相似度： 如果模型的预测概率 y_hat 与真实的类别概率 y 相差较大，意味着模型对正确的类别缺乏置信度，或者将较低的概率分配给正确的类别，那么交叉熵损失会较高。较高的交叉熵表示模型性能较差，模型的预测结果与真实标签的相似度较低。

二分类的 Loss

二分类只有一项是非0

二分类计算方式：y_hat是预测出来的值，y是实际结果。求 y 和 y_hat 的交叉熵获得相似度。如下表。

y_hat	y
log(y_hat)	1
log(1 - y_hat))	0

cross_entropy = 1 * log(y_hat) + 0 * log(1-y_hat))

交叉熵损失：cross_entropy loss = - cross_entropy = - (1 * log(y_hat) + 0 * log(1-y_hat)))

负号是因为输出求log的结果一定是负的（log(0.x)<0），加个负号把损失变为正值是为了更直观的理解，损失最小就是正值最小就行了。

主要这是为了将损失最小化，因为我们的目标是最大化正确类别的预测概率，而最小化错误类别的预测概率。

多分类的 Loss

y_hat是预测出来的值，y是实际结果。求 y 和 y_hat 的交叉熵获得相似度。

cross_entropy = ∑ylog(y_hat)

交叉熵损失：cross_entropy loss = - cross_entropy = - ∑ylog(y_hat)

负号是因为输出求log的结果一定是负的（log(0.x)<0），加个负号把损失变为正值是为了更直观的理解，损失最小就是正值最小就行了。

主要这是为了将损失最小化，因为我们的目标是最大化正确类别的预测概率，而最小化错误类别的预测概率。

计算过程

NLLLoss 和 Cross-Entropy 的区别

在 PyTorch 中，NLLLoss（Negative Log Likelihood Loss）和 CrossEntropyLoss 是两个常用的损失函数，它们在多分类问题中尤为重要。它们之间的主要区别在于它们处理输入数据的方式和它们的应用场景。

NLLLoss（负对数似然损失）:

• 这个损失函数通常用于多分类问题。
• 它期望输入是一个对数概率分布 —— 通常是一个经过 log_softmax 激活函数处理的神经网络输出。
• NLLLoss 并不包含计算概率分布的过程，它只是计算负对数似然。
  

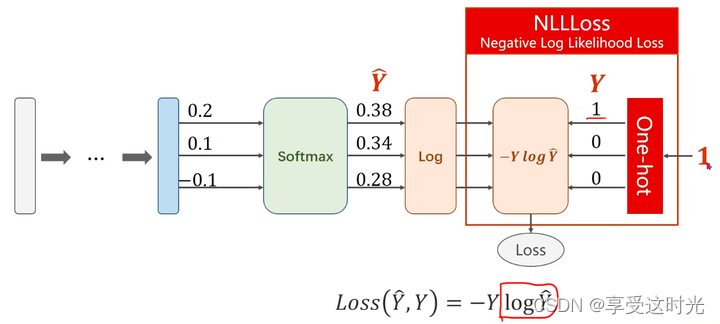
CrossEntropyLoss（交叉熵损失）:

• 这个损失函数同样用于多分类问题。
• 它是 log_softmax 和 NLLLoss 的组合。这意味着，与 NLLLoss 直接使用对数概率分布不同，CrossEntropyLoss 期望的是原始的、未经过任何激活函数处理的输出。
• 它首先内部应用 log_softmax 激活函数，然后应用 NLLLoss。

把 softmax 到输出算loss到整个过程合并起来就是torch.nn.CrossEntropyLoss()

总结一下，如果你的模型的输出是经过 softmax（或 log_softmax）处理的，你应该使用 NLLLoss。如果你的模型输出是原始分数（logits），你应该使用 CrossEntropyLoss，因为它内部会处理激活函数的应用。从实用的角度来看，CrossEntropyLoss 在多数情况下更方便，因为它自动处理了 softmax 激活函数的步骤。

MNIST多分类任务

第一部分 import package

transforms：主要是对图像进行处理
深度学习希望输入是0-1之间，然后是服从正态分布的，这个偏好有几个原因：

• 规范化数据范围
  • 当所有输入[[特征都被规范化到同一范围（如0到1）时，模型训练更加稳定和快速。不同的特征通常具有不同的尺度（例如，一个特征的范围是0到1000，另一个是0到1），这会导致训练过程中梯度下降的问题，因为某些权重的更新可能会比其他权重大得多。
• 避免饱和
  • 深度学习模型中常用的激活函数（如sigmoid和tanh）在输入值很大或很小的时候会饱和。这意味着对于非常大或非常小的输入值，这些函数的梯度几乎为零，这会在反向传播过程中导致梯度消失问题，从而阻碍学习过程。
• 正态分布的好处
  • 让输入数据服从正态分布（或接近正态分布）可以帮助模型更好地学习和理解数据。正态分布的数据具有良好的数学性质，如对称性和固定的均值和方差，这可以简化模型训练过程。
  • 许多优化算法，如梯度下降，假定数据是正态分布的，因此当数据近似于这种分布时，这些算法表现得更好。
• 消除偏差
  • 数据标准化（即将数据转换为均值为0，标准差为1的分布）有助于消除特征间的偏差。这意味着没有任何一个特征会由于它的数值范围大而在模型训练过程中占据主导地位。

其中：

transformer.ToTensor()：把图片 2828，pixel属于0到255。转换为一个张量 128*28，然后 pixel 属于0到1。

• 数据类型转换
  • 将输入数据（通常是 PIL 图像或 NumPy 数组）转换为 torch.FloatTensor。PyTorch 中的张量是深度学习模型的基本数据结构，类似于 NumPy 的数组，但它们可以在 GPU 上运行以加速计算。
• 缩放像素值
  • 自动将像素值从 [0, 255]（通常的图像像素值范围）缩放到 [0.0, 1.0]。这是通过将每个像素值除以 255 实现的。这一步是数据标准化的一部分，有助于模型训练过程的稳定性和效率。
• 调整维度顺序
  • 对于图像数据，PIL 图像和 NumPy 数组通常采用 (高度, 宽度, 颜色通道) 的维度顺序，而 PyTorch 的张量则采用 (颜色通道, 高度, 宽度) 的顺序。transforms.ToTensor() 会自动调整这些维度，以符合 PyTorch 的要求。
    

trasforms.Normalize((0.1307, ), (0.3081, ))：标准正态分布。数据标准化。

第二部分：模型

注意：最后一层不做激活，因为后面调用 torch.nn.CrossEntropyLoss

第三部分：Construct loss and optimizer

训练

测试
max_value, predicted = torch.max(outputs.data, dim=1)
torch.max：返回最大值和对应的下标
dim=1，说明是在行的维度。 0是列，1是行。

代码：MNIST多分类任务

import torch
from torchvision import datasets
from torchvision import transforms
from torch.utils.data import DataLoader
import torch.nn.functional as F
import torch.optim as optim

# prepare dataset
batch_size = 64

transform = transforms.Compose([
    transforms.ToTensor(),
    transforms.Normalize((0.1307, ), (0.3081, ))
])

train_dataset = datasets.MNIST('data/MNIST/', train=True, transform=transform, download=True)
train_loader = DataLoader(dataset=train_dataset, batch_size=batch_size, shuffle=True)

test_dataset = datasets.MNIST('data/MNIST/', train=False, transform=transform, download=True)
test_loader = DataLoader(dataset=test_dataset, batch_size=batch_size, shuffle=False)

# design model
class Net(torch.nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.linear1 = torch.nn.Linear(784, 512)
        self.linear2 = torch.nn.Linear(512, 256)
        self.linear3 = torch.nn.Linear(256, 128)
        self.linear4 = torch.nn.Linear(128, 64)
        self.linear5 = torch.nn.Linear(64, 10)

    def forward(self, x):
        x = x.view(-1, 784)
        x = F.relu(self.linear1(x))
        x = F.relu(self.linear2(x))
        x = F.relu(self.linear3(x))
        x = F.relu(self.linear4(x))
        x = self.linear5(x) # 不用激活函数，因为 torch.nn.CrossEntropyLoss = softmax + nllloss
        return x
    
model = Net()

# construct loss and optimizer
criterion = torch.nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)

# training
def train(epoch):
    running_loss = 0.0
    for batch_idx, data in enumerate(train_loader, 0):
        inputs, target = data
        optimizer.zero_grad()

        outputs = model(inputs)
        loss = criterion(outputs, target)
        loss.backward()
        optimizer.step()

        running_loss += loss.item()

        if batch_idx % 300 == 299:
            print('[%d, %5d] loss: %.3f' % (epoch+1, batch_idx+1, running_loss/300))
            running_loss = 0.0

# test
def test():
    correct = 0
    total = 0
    with torch.no_grad():
        for data in test_loader:
            inputs, labels = data
            outputs = model(inputs)
            _, predicted = torch.max(outputs.data, dim=1)
            total += labels.size(0)
            correct += (predicted == labels).sum().item()
        print('Accuracy on test set: %d %%' %(100*correct/total))


if __name__ == '__main__':
    for epoch in range(10):
        train(epoch)
        if epoch % 10 == 0:
            test()

P9 作业：Kaggle Otto Group Product Classification Challenge

数据下载地址：https://www.kaggle.com/c/otto-group-product-classification-challenge/data
百度网盘链接下载： https://pan.baidu.com/s/1g8rshQdwba7ctwLmzl69Qw?pwd=4nd4 提取码: 4nd4

import torch
import pandas as pd
from torch.utils.data import Dataset, DataLoader
from sklearn.preprocessing import StandardScaler        # pip install scikit-learn
import torch.nn.functional as F
import torch.optim as optim
import matplotlib.pyplot as plt

class OttoDataset(Dataset):
    def __init__(self, feature_filepath, label_filepath=None, mode='train', scaler=None):
        super(OttoDataset, self).__init__()

        # Load the dataset into a pandas dataframe.
        data = pd.read_csv(feature_filepath)

        if mode == 'train':
            # Extract the numeric part of the class labels, convert to integers, and shift to zero-based indexing.
            self.labels = torch.tensor(data.iloc[:, -1].apply(lambda x: int(x.split('_')[-1]) - 1).values, dtype=torch.long)
            
            # Initialize the StandardScaler.
            # StandardScaler will normalize the features (i.e., each column of the dataset)
            # by subtracting the mean and dividing by the standard deviation.
            # This centers the feature columns at mean 0 with standard deviation 1.
            self.scaler = StandardScaler()

            # Select all columns except 'id' and 'target' for features.
            # Then apply the scaler to standardize them.
            features = data.iloc[:, 1:-1].values
            self.features = torch.tensor(self.scaler.fit_transform(features), dtype=torch.float32)

        elif mode == 'test':
            features = data.iloc[:, 1:].values

            # Apply the same scaling as on the training set to the test set features. use self.scaler.transform
            self.scaler = scaler if scaler is not None else StandardScaler()
            self.features = torch.tensor(self.scaler.transform(features), dtype=torch.float32)
            
            if label_filepath is not None:
                label_data = pd.read_csv(label_filepath)
                # Assuming the first column after 'id' are one-hot encoded class labels,
                # find the index of the max value in each row which corresponds to the predicted class.
                self.labels = torch.tensor(label_data.iloc[:, 1:].values.argmax(axis=1), dtype=torch.long)

            else:
                self.labels = None

        # If neither 'train' nor 'test' mode is specified, raise an error.
        else:
            raise ValueError("Mode must be 'train' or 'test'")
        
        # Store the length of the dataset.
        self.len = len(self.features)

    def __len__(self):
        # When len(dataset) is called, return the length of the dataset.
        return self.len
    
    def __getitem__(self, index):
        # This method retrieves the features and label of a specified index.
        return self.features[index], self.labels[index] if self.labels is not None else -1
    

class FullyConnectedModel(torch.nn.Module):
    def __init__(self, input_features, output_classes):
        super(FullyConnectedModel, self).__init__()
        
        # 定义网络层
        self.fc1 = torch.nn.Linear(input_features, 128)
        self.fc2 = torch.nn.Linear(128, 64)
        self.fc3 = torch.nn.Linear(64, 32)
        self.fc4 = torch.nn.Linear(32, output_classes)

        # 可以选择增加更多的层

        # 定义 dropout 层，可以减少过拟合
        self.dropout = torch.nn.Dropout(p=0.3)

        # 定义 batchnorm 层，帮助稳定学习过程
        self.batchnorm1 = torch.nn.BatchNorm1d(128)
        self.batchnorm2 = torch.nn.BatchNorm1d(64)
        self.batchnorm3 = torch.nn.BatchNorm1d(32)

    def forward(self, x):
        x = F.relu(self.batchnorm1(self.fc1(x)))
        x = self.dropout(x)
        x = F.relu(self.batchnorm2(self.fc2(x)))
        x = self.dropout(x)
        x = F.relu(self.batchnorm3(self.fc3(x)))
        x = self.dropout(x)
        x = self.fc4(x)
        return x
    

def train(epoch, train_loader, model, criterion, optimizer):
    model.train()
    running_loss = 0.0
    for batch_idx, data in enumerate(train_loader, 0):
        inputs, targets = data

        inputs = inputs.to(device)
        targets = targets.to(device)

        optimizer.zero_grad()
        outputs = model(inputs)
        loss = criterion(outputs, targets)
        loss.backward()
        optimizer.step()

        running_loss += loss.item()

        if batch_idx % 300 == 0:
            print('Epoch:[{}/{}], Loss:{:.4f}'.format(epoch, batch_idx, running_loss/300))

    # 计算平均损失
    average_loss = running_loss / len(train_loader)
    return average_loss


def test(test_loader, model):
    model.eval()
    correct = 0.0
    total = 0
    with torch.no_grad():
        for inputs, targets in test_loader:
            outputs = model(inputs)
            inputs = inputs.to(device)
            targets = targets.to(device)
            _, predicted = torch.max(outputs.data, dim=1)
            total += targets.size(0)
            correct += (predicted == targets).sum().item()
    accuracy = 100 * (correct / total)
    print("Accuracy on test data is {:.2f}".format(accuracy))
    return accuracy



if __name__ == '__main__':
    device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')

    # Prepare dataset
    train_dataset = OttoDataset(feature_filepath='data/Otto/train.csv', mode='train')
    scaler = train_dataset.scaler
    test_dataset = OttoDataset(feature_filepath='data/Otto/test.csv', label_filepath='data/Otto/otto_correct_submission.csv', mode='test', scaler=scaler)

    train_loader = DataLoader(dataset=train_dataset, batch_size=64, shuffle=True, num_workers=0)
    test_loader = DataLoader(dataset=test_dataset, batch_size=64, shuffle=False, num_workers=0)
    
    # Design model
    model = FullyConnectedModel(input_features=93, output_classes=9).to(device)

    # Construct loss and optimizer
    criterion = torch.nn.CrossEntropyLoss().to(device)
    optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
    scheduler = torch.optim.lr_scheduler.StepLR(optimizer, step_size=25, gamma=0.1)

    
    # Train and Test
    train_losses = []
    test_accuracies = []

    num_epochs = 100
    for epoch in range(num_epochs):
        train_loss = train(epoch, train_loader, model, criterion, optimizer)
        train_losses.append(train_loss)
        
        if epoch % 2 == 0 or epoch == num_epochs-1:
            test_accuracy = test(test_loader, model)
            test_accuracies.append(test_accuracy)


        # Update the learning rate
        scheduler.step()
        
    # Save model parameters for future use
    torch.save(model.state_dict(), 'model/09_kaggle_OttoDataset_model.pth')

    # Visualize
    plt.figure(figsize=(12, 5))

    # Loss Curve
    plt.subplot(1, 2, 1)
    plt.plot(train_losses, label='Train Loss')
    plt.title('Training Loss')
    plt.xlabel('Epoch')
    plt.ylabel('Loss')
    plt.legend()

    # Accuracy Curve
    plt.subplot(1, 2, 2)
    plt.plot(range(0, 101, 2), test_accuracies, label='Test Accuracy')  # Adjust x-axis for test accuracy
    plt.title('Testing Accuracy')
    plt.xlabel('Epoch')
    plt.ylabel('Accuracy (%)')
    plt.legend()

    plt.show()