机器学习笔记 soft-DTW（论文笔记 A differentiable loss function for time-series）

UQI-LIUWJ

已于 2022-01-23 14:11:21 修改

阅读量7.2k

点赞数 15

分类专栏：论文笔记机器学习文章标签：机器学习算法人工智能

于 2022-01-22 20:57:50 首次发布

本文链接：https://blog.csdn.net/qq_40206371/article/details/122568648

版权

论文笔记同时被 2 个专栏收录

362 篇文章

订阅专栏

机器学习

157 篇文章

订阅专栏

本文介绍了soft-DTW算法，它是DTW算法的一种可微版本，适用于神经网络中的时间序列对比。文章详细解释了soft-DTW的基本原理，包括其如何通过使用soft-min函数替代传统的min函数来实现可微性，并给出了前向传播和反向传播的具体公式。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1 soft-DTW来由

DTW 算法通过动态规划求解了两个序列的相似度。这个过程1是离散的，不可微的。如果要将其应用作为神经网络的损失函数，这是不行的。因为神经网络通过对损失函数结果进行梯度下降的方法，更新参数，要求损失函数可微。

2 符号说明

论文“A differentiable loss function for time-series”（2017 ICML）中使用了 Soft minimum 来代替 DTW minimum

对于两个序列和，我们定义代价矩阵，其中δ是可微代价函数（某一时刻x上的p维信息+某一时刻y上的p维信息——>一个实数值）【通常δ(·,·)可以用欧几里得距离】

3 soft-DTW原理

定义集合，为路径上的代价和 $r_{i,j}$ 组成的集合（从(0,0)到(i,j)的最小开销路径的cost）

如果是DTW，那么它的动态规划式子为

如1所说，由于min是一个离散的过程，不可微，所以这导致了DTW的离散。

于是Soft-DTW使用了连续的soft-min

当γ=0的时候，就是DTW，否则他就是一个可微的式子

（在max函数的平滑（log-sum-exp trick）_UQI-LIUWJ的博客-CSDN博客中，我们知道

$log(\sum_{i \in [1,n]}e^{x_i})=log(\sum_{i \in [1,n],i \ne j}e^{x_i}+e^{x_j}) \approx log(e^{x_j})=x_j=max \{x_1,\dots,x_n \}$

那么这里也是类似的

$min(a_1,a_2,\dots,a_n)=-max(-a_1,-a_2,\dots,-a_n)$

$=-log (\sum_{i \in [1,n]} e^{-a_i})$

$=-log [\sum_{i \in [1,n]} (e^\frac{{-a_i}}{\gamma})^\gamma]$

这里这篇论文做了一个近似

$\approx -log [\sum_{i \in [1,n]} (e^\frac{{-a_i}}{\gamma})]^\gamma$

也就等于了

3.1 前向传播

定义，这是一个集合，其中的每一个元素A是一个矩阵，该矩阵表示两个时间序列x和y之间的对齐矩阵（alignment matrix）

对于一个特定的对齐矩阵，A中只有在(1,1)到(n,m)路径上的点(i,j)，其 $a_{i,j}$ =1，其他点的 $a_{i,j}$ 都是0。

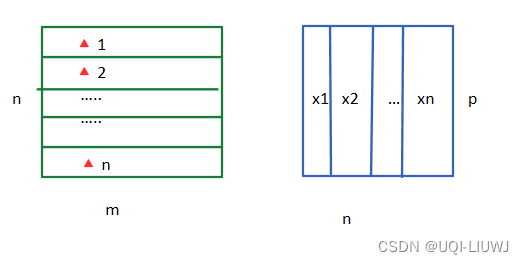
以DTW中出现过的图为例，那种情况下的A矩阵，在红色箭头上的(i,j)，其 $a_{i,j}$ =1，其余点的 $a_{i,j}$ 均为0DTW 笔记： Dynamic Time Warping 动态时间规整（&DTW的python实现）_UQI-LIUWJ的博客-CSDN博客

换句话说， $A_{n,m}$ 中包含了所有(1,1)到(n,m)的路径（每个路径是一个矩阵，每个矩阵只有路径上的元素为1）

于是矩阵内积<A，Δ(x,y)>表示这条路径下的代价和（非这条路径上的点乘0，这条路径上的点乘1，再求和）

于是，soft-dtw的目标函数为

3.1.1 算法伪代码

如果γ=0的时候，也就退化为了DTW，这里不同的是，我们需要关注γ＞0的情况

3.2 反向传播

soft-DTW的目的是为了计算时间序列x和时间序列y之间的动态扭曲距离，y是目标序列的话，我们反向传播计算的是对时间序列x的梯度，也即

通过链式法则，我们有

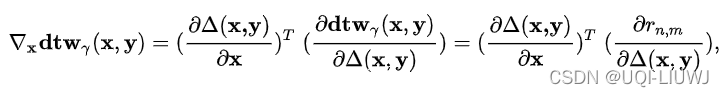
这里的分子和分母都是矩阵，所以线性代数笔记：标量、向量、矩阵求导_UQI-LIUWJ的博客-CSDN博客

也就是在我们的问题中， $\frac{\partial \Lambda_i}{\partial x_j}$ 都是一个p×m维矩阵，那么整体上是一个np×nm的矩阵（记🔺相对于x的雅可比矩阵）

对于第二项

由于

同样地根据链式法则有：

定义元素

我们令

所以有：

当 $\Delta$ 为欧几里得距离的时候，对于任意n×m维度的矩阵，有：

3.2.1 反向传播的优化

对于这个式子，我们进行反向传播的时候，如果使用自动求导机制，那每一个 $e_{i,j}$ 的计算，都需要重新从 $e_{1,1}$ 开始计算，计算到 $e_{i,j}$ 为止，所以每一个 $e_{i,j}$ 都需要 $O(mn)$ 的时间复杂度，而每次反向传播都需要计算一次E矩阵，所以每次反向传播计算E就需要 $O(m^2n^2)$ 的时间复杂度