1 降维
1.1 高维数据
我们会经常看到很多高维数据,但是这些高维数据并不一定需要这么多维度来表示。
比如左图这样的图像并不一定要用三维向量表示,对其稍加修改,便可以用右图的二维向量表示了
再举一个例子,我们知道MNIST数据集是28*28维的向量组成的,但实际上我们并不一定要用这么高维的向量来表示MNIST
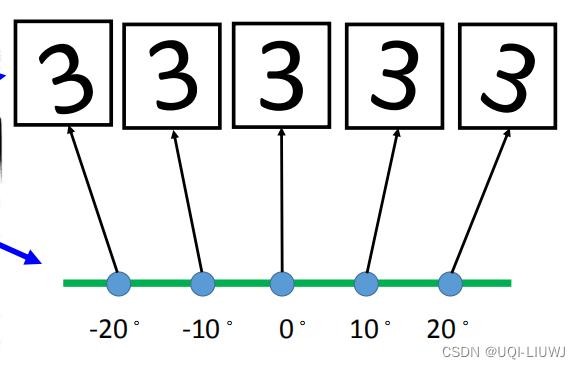
举一个最极端的例子
如果一个数据集里面只有3,但是是不同方向的3,那么其实用一个维度表示就ok了:3的朝向
1.2 降维
降维的核心思想就是,输入原始数据X之后,通过降维的函数,得到数据Z。数据Z的维度比X小很多。且数据Z尽可能地保持原来X的信息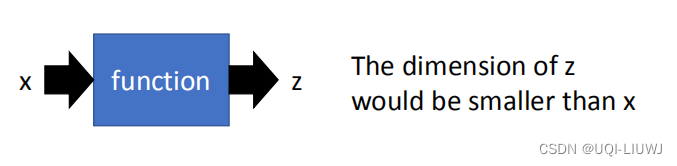
2 主成分分析PCA
2.1 先考虑一维的情况
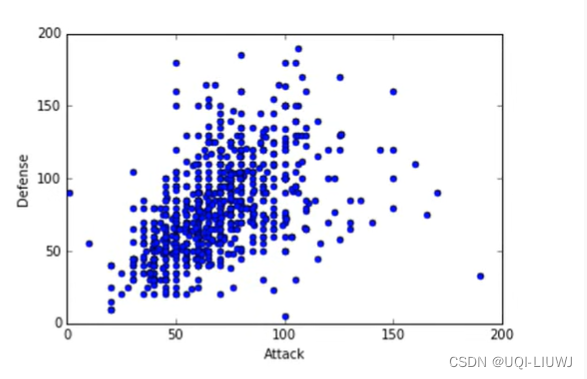
我们有一堆向量X,我们希望用一维表示这些X,那么这一维的坐标轴怎么找呢?
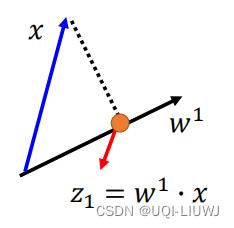
回顾一个线性代数的知识:假设我们找到了坐标轴向量w(w是单位向量),向量x在w上的投影 就是x和w的内积
那么在这里,我们不希望降维之后的点靠得太近,希望他们尽量互相原理一些。
用数学的方式表达,就是希望方差
越大越好
2.2 延伸到多维
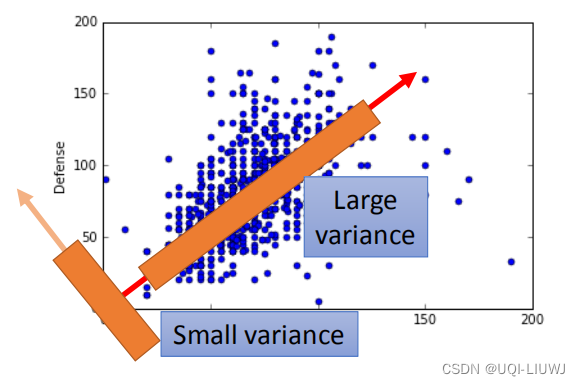
当然,现实生活中的数据可能维度更高,降至一维是不现实的。此时我们可能就需要多个单位向量
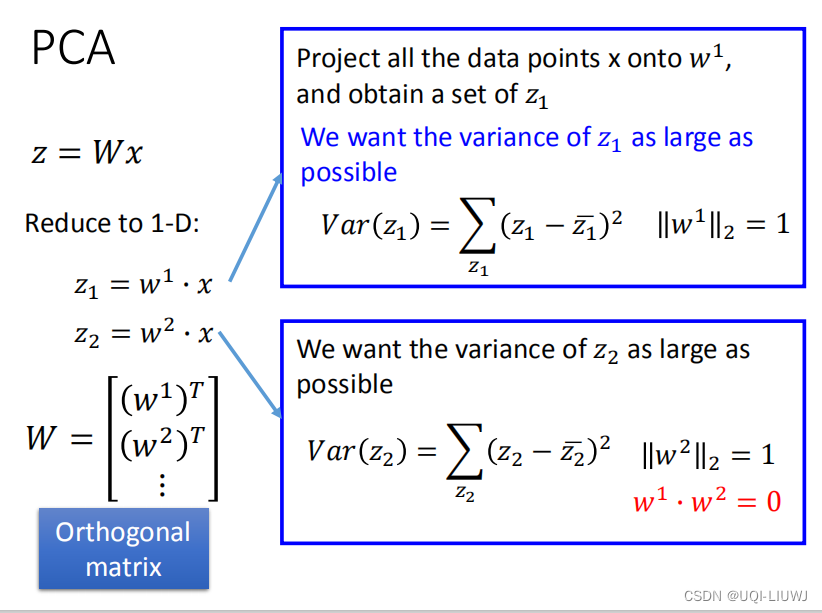
我们要求x在各个 上的投影,方差都要越大越好。
当然,如果只要求方差越大越好是不行的,因为这样的话会导致,于是我们希望不同的
之间两两正交。
——>主成分的标准
- 互不相关
- 方差尽可能地大
2.3 数学推导PCA
2.3.1 第一个w
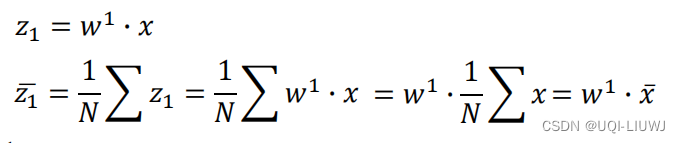
然后我们看Var(z1),我们希望他越大越好
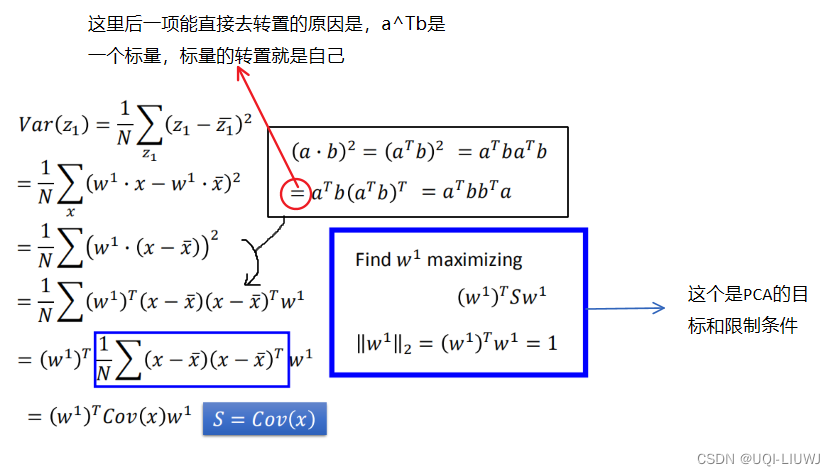
再回顾一个线性代数的知识 :
- 协方差矩阵 S=Cov(x)是一个对称+半正定的矩阵。
- 对称+半正定的矩阵有非零特征值
——> 协方差矩阵有非零特征值
我们的目标就是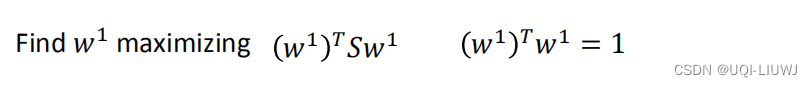
使用拉格朗日乘子:
求关于的偏导:
——> ——>α是矩阵S的一个特征值
将上式带回到我们希望最大化的式子里,有:
【后两项的乘积为1】
所以最大化 也就是最大化α,即找到S最大的特征值
所以是协方差矩阵S最大的特征值λ1对应的特征向量
2.3.2 第二个w
和第一个w的约束方程类似,知识多了一个约束条件,就是正交
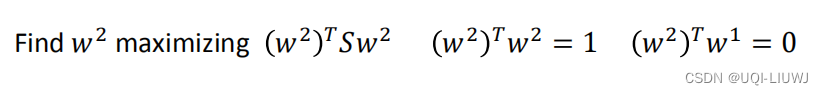
同样用拉格朗日算子,有:
对求偏导,有
上式同时左乘一个,有:
其中
所以
由于是标量,所以
S是对称矩阵,所以
所以β=0
也就是说
为了让越大越好,所以w2对应的alpha是第二大的特征值(因为第一大的w1已经用掉了)
所以是协方差矩阵S第二大的特征值λ2对应的特征向量
2.4 PCA:去关联性
通过PCA之后,z的协方差矩阵是一个对角阵。

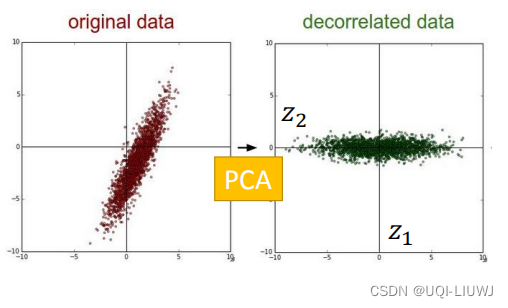
2.4.1 去关联性推导
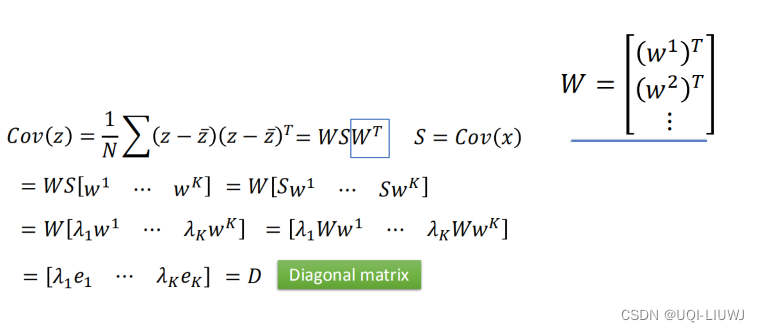
2.5 从矩阵层面看PCA
假设我们一个向量x可以写成如下形式
那么我们可以用
来表示向量x
转换一下,我们希望:
也即: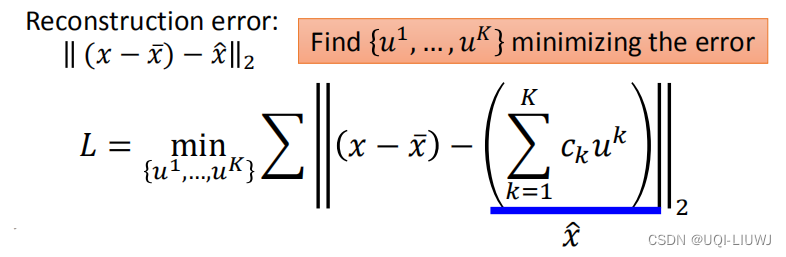
每一个都是一列,所以我们可以转化成矩阵形式:

用SVD求解U和C矩阵:(Σ矩阵放在那边都可以)
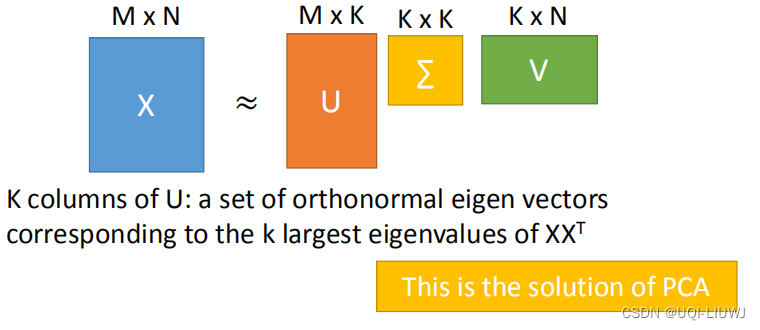
效果和数学推导的PCA是一样的
2.6 从autoencoder层面看PCA
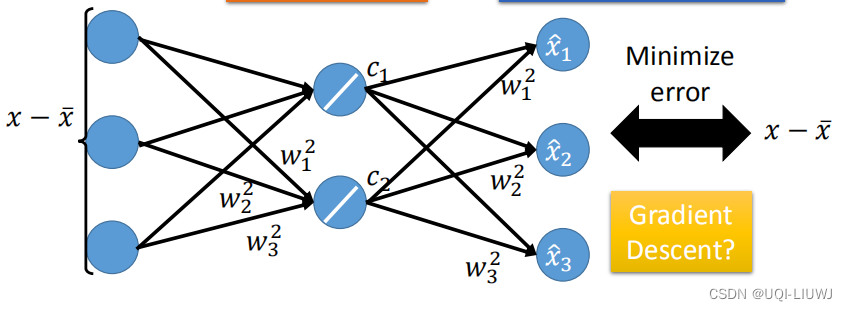
PCA可以看成是一个有一层隐藏层的神经网络(激活函数是线性的)
如果我们降维后的K个基为
,那么我们希望 <->两边的内容相逼近
又这K个基两两正交,所以我们可以用如下方式求每个Ck

- 把
的每一维看成是一个神经元,那么
就是权重,我们便得到了输入层——>隐藏层的部分
- 又有
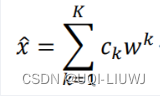 ,所以我们得到了隐藏层——>输出层 。所以在一定程度上可以看成autoencoder (只不过PCA对应的autoencoder需要
,所以我们得到了隐藏层——>输出层 。所以在一定程度上可以看成autoencoder (只不过PCA对应的autoencoder需要两两正交)
3 一些应用
3.1 PCA+MNIST
MNIST 每一张图是一个28*28=784维的向量,我们用PCA,选择前30大特征值对应的特征向量,作为主成分,其可视化结果如下:

3.2 PCA+FACE
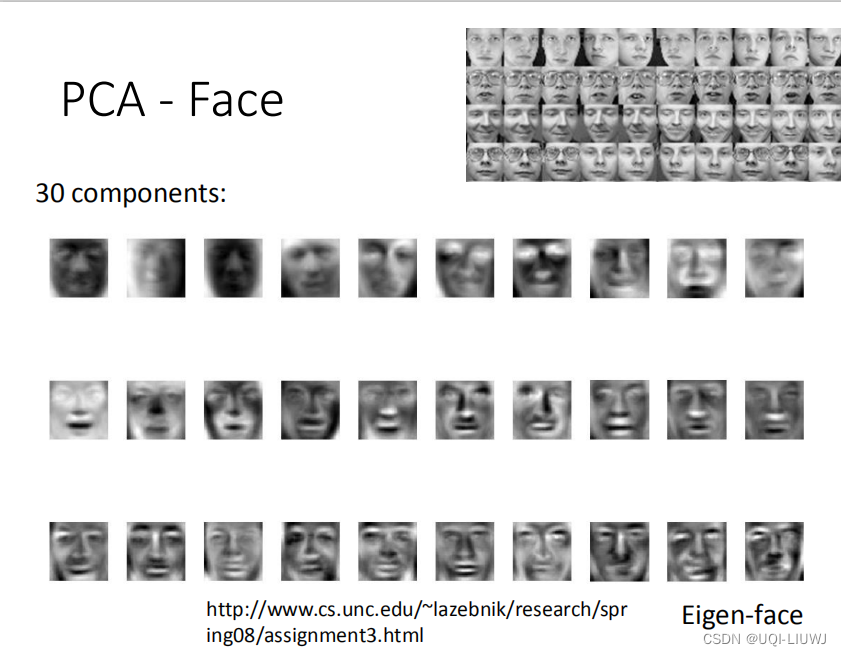
3.3 为什么3.2和3.1的主成分都不是某一个部分,而也是类数字/类人脸呢?
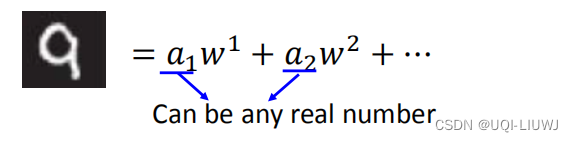
因为这边的的元素没有限制,可正可负,所以可能出现“两个主成分都是人脸,然后正好相减抵消”的情况。
3.3.1 一种解决方法 非负矩阵分解
一种解决方法是非负矩阵分解,加上约束条件:元素均非负
可以看到使用了NMF非负矩阵分解之后,主成分就是一个一个小组件了,而不是类数字/类人脸的东西


参考内容ML Lecture 13: Unsupervised Learning - Linear Methods - YouTube









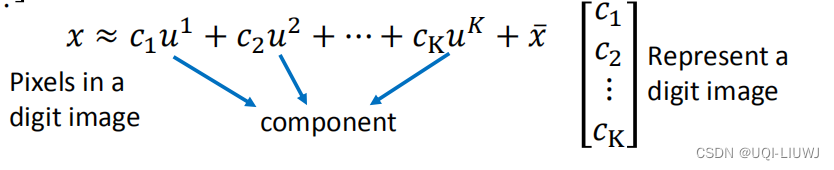
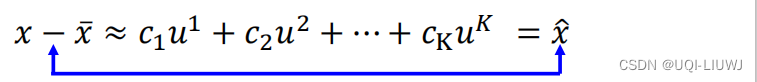
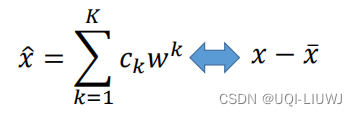















 2万+
2万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










