永磁同步电机控制系统——模型预测控制（MPC）

1 MPC原理

模型预测控制（Model Predictive Control, MPC）是近年来被广泛讨论的反馈控制策略。模型预测控制的机理可描述为：在每一采样时刻，根据获得的当前测量信息，在线求解一个有限时域开环优化问题，并将得到的控制序列的第一个元素作用于被控对象。在下一个采样时刻，重复上述过程，用新的测量值刷新优化问题并重新求解¹。

MPC与传统控制方法相比的几大优势

1. MPC在线求解开环优化问题，获得最优控制律。而传统控制方法通常离线求解一个反馈控制律，并将其一直作用于系统。
2. MPC在处理非线性、等式约束和不等式约束问题上具有较大优势。

2 MPC求解无约束问题步骤

为引入积分以减小或者消除静态误差，使用增量式状态空间模型：
$$\Delta x(k+1)=A\Delta x(k)+B_u\Delta u(k)+B_d\Delta d(k)\text{\hspace{1em}(1)}$$

$$y_c(k)=C_c\Delta x(k)+y_c(k-1)\text{\hspace{1em}(2)}$$

在当前时刻$k$，测量值为$x(k)$，计算$\Delta x(k)=x(k)-x(k-1)$，将其作为预测系统未来动态的起点，预测未来$p$步的状态增量。
$$\begin{array}{rl}\Delta x(k+1|k)=& A\Delta x(k)+B_u\Delta u(k)+B_d\Delta d(k)\\ \Delta x(k+2|k)=& A\Delta x(k+1|k)+B_u\Delta u(k+1)+B_d\Delta d(k+1)\\ =& A^2\Delta x(k)+A{B}_u\Delta u(k)+B_u\Delta u(k+1)+A{B}_d\Delta d(k)\\ & ⋮\\ \Delta x(k+p|k)=& A\Delta x(k+p-1|k)+B_u\Delta u(k+p-1)+B_d\Delta d(k+p-1)\\ =& A^p\Delta x(k)+A^{p-1}{B}_u\Delta u(k)+A^{p-2}{B}_u\Delta u(k+1)\\ & +...+A^{p-m}{B}_u\Delta u(k+m-1)+A^{p-1}{B}_d\Delta d(k)\end{array}\text{\hspace{1em}(3)}$$
进一步，由输出方程可以预测未来$p$步被控输出
$$\begin{array}{rl}{y}_c(k+1|k)=& C_c\Delta x(k+1|k)+y_c(k)\\ =& C_{c}A\Delta x(k)+C_c{B}_u\Delta u(k)+C_c{B}_d\Delta d(k)+y_c(k)\\ & ⋮\\ y_c(k+p|k)=& C_c\Delta x(k+p|k)+y_c(k+p-1|k)\\ =& \sum _{i=1}^p{C}_c{A}^i\Delta x(k)+\sum _{i=1}^p{C}_c{A}^{i-1}{B}_u\Delta u(k)\\ & +\sum _{i=1}^{p-1}{C}_c{A}^{i-1}{B}_u\Delta u(k+1)+...\\ & +\sum _{i=1}^{p-m+1}{C}_c{A}^{i-1}{B}_u\Delta u(k+m-1)\\ & +\sum _{i=1}^p{C}_c{A}^{i-1}{B}_d\Delta d(k)+y_c(k)\end{array}\text{\hspace{1em}(4)}$$
定义$p$步预测输出向量和$m$步预测输入向量为：

$$Y_p(k+1|k)={\left[\begin{array}{c}{y}_c(k+1|k)\\ y_c(k+2|k)\\ ⋮\\ y_c(k+p|k)\end{array}\right]}_{p\times 1},\Delta U(k)={\left[\begin{array}{c}\Delta u(k)\\ \Delta u(k+1)\\ ⋮\\ \Delta u(k+m-1)\end{array}\right]}_{m\times 1}\text{\hspace{1em}(5)}$$
注：矩阵的下标表示矩阵中向量或标量的个数。例如，上式中，$p\times 1$仅表示$Y_c(k+1|k)$矩阵中$y_c$的个数。

系统未来$p$步预测输出为：

$$Y_p(k+1|k)=S_x\Delta x(k)+\mathrm{I}{y}_c(k)+S_d\Delta d(k)+S_u\Delta U(k)\text{\hspace{1em}(6)}$$
其中，

$$\begin{gathered} S_x={\left[\begin{array}{c}{C}_{c}A\\ {\sum }_{i=1}^2{C}_c{A}^i\\ ⋮\\ {\sum }_{i=1}^p{C}_c{A}^i\end{array}\right]}_{p\times 1},\mathrm{I}={\left[\begin{array}{c}{I}_{n_c\times n_c}\\ I_{n_c\times n_c}\\ ⋮\\ I_{n_c\times n_c}\end{array}\right]}_{p\times 1},S_d={\left[\begin{array}{c}{C}_c{B}_d\\ {\sum }_{i=1}^2{C}_c{A}^{i-1}{B}_d\\ ⋮\\ {\sum }_{i=1}^p{C}_c{A}^{i-1}{B}_d\end{array}\right]}_{p\times 1}, \\ {S}_u={\left[\begin{array}{ccccc}{C}_c{B}_u& 0& 0& \cdots & 0\\ {\sum }_{i=1}^2{C}_c{A}^{i-1}{B}_u& C_c{B}_u& 0& \cdots & 0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ {\sum }_{i=1}^m{C}_c{A}^{i-1}{B}_u& {\sum }_{i=1}^{m-1}{C}_c{A}^{i-1}{B}_u& \cdots & \cdots & C_c{B}_u\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ {\sum }_{i=1}^p{C}_c{A}^{i-1}{B}_u& {\sum }_{i=1}^{p-1}{C}_c{A}^{i-1}{B}_u& \cdots & \cdots & {\sum }_{i=1}^{p-m+1}{C}_c{A}^{i-1}{B}_u\end{array}\right]}_{p\times m}\text{\hspace{1em}(7)} \end{gathered}$$
接下来，要明确优化问题的数学描述。我们希望被控输出接近参考输入，同时希望控制变化不要太大，建立如下目标函数：
$$J=\sum _{i=1}^p{\Vert \begin{array}{c}{\Gamma }_{y,i}{y}_c(k+i|k)-r(k+1)\end{array}\Vert }^2+\sum _{i=1}^m{\Vert \begin{array}{c}{\Gamma }_{u,i}\Delta u(k+i-1)\end{array}\Vert }^2\text{\hspace{1em}(8)}$$
其中，${\Gamma }_{y,i}=diag({\Gamma }_{y_1,i},{\Gamma }_{y_2,i},\cdots ,{\Gamma }_{y_{nc},i}),{\Gamma }_{u,i}=diag({\Gamma }_{u_1,i},{\Gamma }_{u_2,i},\cdots ,{\Gamma }_{u_{nu},i})$。${\Gamma }_{y_j,i}$是在预测时刻$i$对预测控制输出第$j$个分量误差的加权因子，加权因子越大，表明期望控制输出越接近给定的参考输入；${\Gamma }_{u_j,i}$是在预测时刻$i$对控制增量第$j$个分量的加权因子，控制加权因子越大，表明期望的控制动作变化越小。

优化问题1：
$$\underset{\Delta U(k)}{\min }J(x(k),\Delta U(k),m,p)\text{\hspace{1em}(9)}$$
满足动力学方程$(i=0,1,\cdots ,p)$：
$$\begin{array}{rl}\Delta x(k+i+1|k)& =A\Delta x(k+i|k)+B_u\Delta u(k+i)+B_d\Delta d(k+i),\\ \Delta x(k|k)& =\Delta x(k),\\ y_c(k+i|k)& =C_c\Delta x(k+i|k)+y_c(k+i-1|k)\end{array}\text{\hspace{1em}(10)}$$
其中，

$$\begin{array}{rl}J(x(k),\Delta U(k),m,p)=& {\Vert \begin{array}{c}{\Gamma }_y{Y}_p(k+1|k)-R(k+1)\end{array}\Vert }^2+{\Vert \begin{array}{c}{\Gamma }_u\Delta U(k)\end{array}\Vert }^2\end{array}\text{\hspace{1em}(11)}$$
其中，$Y_p(k+1|k)$由式$(5)$给出，加权矩阵为：
$$\begin{gathered} {\Gamma }_y=diag({\Gamma }_{y,1},{\Gamma }_{y,2},\cdots ,{\Gamma }_{y,p}), \\ {\Gamma }_u=diag({\Gamma }_{u,1},{\Gamma }_{u,2},\cdots ,{\Gamma }_{u,m})\text{\hspace{1em}(12)} \end{gathered}$$
参考输入序列为：
$$R(k+1)=\left[\begin{array}{c}r(k+1)\\ r(k+2)\\ ⋮\\ r(k+p)\end{array}\right]\text{\hspace{1em}(13)}$$
求解1：

为方便求解，定义辅助变量：

$$\rho =\left[\begin{array}{c}{\Gamma }_y{Y}_p(k+1|k)-R(k+1)\\ {\Gamma }_u\Delta U(k)\end{array}\right]\text{\hspace{1em}(14)}$$
则目标函数$(11)$改写为：
$$J(x(k),\Delta U(k),m,p)={\rho }^T\rho \text{\hspace{1em}(15)}$$
将预测方程$(6)$代入$(14)$：
$$\begin{array}{rl}\rho =& \left[\begin{array}{c}{\Gamma }_y(S_x\Delta x(k)+\mathrm{I}{y}_c(k)+S_d\Delta d(k)+S_u\Delta U(k))-R(k+1)\\ {\Gamma }_u\Delta U(k)\end{array}\right]\\ =& \left[\begin{array}{c}{\Gamma }_y{S}_u\\ {\Gamma }_u\end{array}\right]\Delta U(k)-\left[\begin{array}{c}{\Gamma }_y(\stackrel{E_p(k+1|k)}{\overbrace{R(k+1)-S_x\Delta x(k)-\mathrm{I}{y}_c(k)-S_d\Delta d(k)}})\\ 0\end{array}\right]\\ =& \underset{Az}{\underbrace{\left[\begin{array}{c}{\Gamma }_y{S}_u\\ {\Gamma }_u\end{array}\right]\Delta U(k)}}-\underset{b}{\underbrace{\left[\begin{array}{c}{E}_p(k+1|k)\\ 0\end{array}\right]}}\\ =& Az-b\end{array}\text{\hspace{1em}(16)}$$

其中，

$$z=\Delta U(k)，A=\left[\begin{array}{c}{\Gamma }_y{S}_u\\ {\Gamma }_u\end{array}\right],b=\left[\begin{array}{c}{E}_p(k+1|k)\\ 0\end{array}\right]\text{\hspace{1em}(17)}$$

$$E_p(k+1|k)=R(k+1)-S_x\Delta x(k)-\mathrm{I}{y}_c(k)-S_d\Delta d(k)\text{\hspace{1em}(18)}$$

因此优化问题1变为：
$$\underset{z}{\min }{\rho }^T\rho ,其中\rho =Az-b\text{\hspace{1em}(19)}$$
极值条件为：
$$\frac{\mathrm{d}{\rho }^T\rho }{\mathrm{d}z}=2(\frac{\mathrm{d}\rho }{\mathrm{d}z}{)}^T,\rho =2A^T(Az-b)=0\text{\hspace{1em}(20)}$$
得极值解为

$$z^{\ast }=(A^{T}A{)}^{-1}{A}^{T}b\text{\hspace{1em}(21)}$$
又由于
$$\frac{{\mathrm{d}}^2({\rho }^T\rho )}{\mathrm{d}{z}^2}=2A^{T}A>0\text{\hspace{1em}(22)}$$
则式$(21)$是取得最小值的解。将式$(17)$代入式$(21)$，得到优化问题1的最优解，即$k$时刻的最优控制序列为
$$\Delta U^{\ast }(k)=(S_u^T{\Gamma }_y^T{\Gamma }_y{S}_u+{\Gamma }_u^T{\Gamma }_u{)}^{-1}{S}_u^T{\Gamma }_y^T{\Gamma }_y{E}_p(k+1|k)\text{\hspace{1em}(23)}$$
其中$E_p(k+1|k)$由式$(18)$计算。

将最优控制序列的第一个元素将作用于系统，即
$$\begin{array}{rl}\Delta u(k)=& {\left[\begin{array}{cccc}{I}_{n_c\times n_c}& 0& \cdots & 0\end{array}\right]}_{1\times m}\Delta U\ast (k)\\ =& {\left[\begin{array}{cccc}{I}_{n_c\times n_c}& 0& \cdots & 0\end{array}\right]}_{1\times m}(S_u^T{\Gamma }_y^T{\Gamma }_y{S}_u+{\Gamma }_u^T{\Gamma }_u{)}^{-1}{S}_u^T{\Gamma }_y^T{\Gamma }_y{E}_p(k+1|k)\end{array}\text{\hspace{1em}(24)}$$
定义预测控制增益

$$K_{mpc}={\left[\begin{array}{cccc}{I}_{n_c\times n_c}& 0& \cdots & 0\end{array}\right]}_{1\times m}(S_u^T{\Gamma }_y^T{\Gamma }_y{S}_u+{\Gamma }_u^T{\Gamma }_u{)}^{-1}{S}_u^T{\Gamma }_y^T{\Gamma }_y\text{\hspace{1em}(25)}$$
那么控制增量可由下式计算

$$\Delta u(k)=K_{mpc}{E}_p(k+1|k)\text{\hspace{1em}(26)}$$
算法总结：

1. 初始化：设定预测时域p和控制时域m，初始值$u(-1)=0$，$x(-1)=0$，由式$(7)$计算$S_x$，$I$，$S_d$和$S_u$，由式$(25)$计算$K_{mpc}$。
2. $k\ge 0$时刻，得到测量值$x(k)$和$d(k)$。由式$(2)$计算$y_c(k)$，计算$\Delta x(k)=x(k)-x(k-1)$。
3. 由式$(18)$计算误差 $E_p(k+1|k)$。
4. 由式$(26)$计算控制变量增量 $\Delta u(k)$。
5. 将$u(k)=u(k-1)+\Delta u(k)$作用于系统。
6. 在$k+1$时刻，测量$x(k+1)$和$d(k+1)$的值，并且令$k=k+1$，返回第2步。

• 注：如果采用时不变加权因子，则$K_{mpc}$可离线计算，否则$K_{mpc}$需在循环内进行，即在线计算

3 基于MPC的电流环设计

永磁同步电机电压方程如下：
$$\begin{array}{rl}\frac{\mathrm{d}{i}_d}{\mathrm{d}t}=& -\frac{R_s}{L_d}{i}_d+\frac{{\omega }_e{L}_q}{L_d}{i}_q+\frac{u_d}{L_d}\\ \frac{\mathrm{d}{i}_q}{\mathrm{d}t}=& -\frac{{\omega }_e{L}_d}{L_q}{i}_d-\frac{R_s}{L_q}{i}_q+\frac{u_q}{L_q}-\frac{{\omega }_e{\psi }_m}{L_q}\end{array}\text{\hspace{1em}(27)}$$

离散化并改写成增量式
$$\Delta x(k+1)=A\Delta x(k)+B_u\Delta u(k)\text{\hspace{1em}(28)}$$
其中，
$$\begin{gathered} x=\left[\begin{array}{cc}{i}_d& i_q\end{array}\right],u=\left[\begin{array}{cc}{u}_d& u_q\end{array}\right] \\ A=\left[\begin{array}{cc}1-\frac{R_s{T}_s}{L_d}& \frac{{\omega }_e{L}_q{T}_s}{L_d}\\ -\frac{{\omega }_e{L}_d{T}_s}{L_q}& 1-\frac{R_s{T}_s}{L_q}\end{array}\right],B_u=\left[\begin{array}{cc}\frac{T_s}{L_d}& \frac{T_s}{L_q}\end{array}\right]\text{\hspace{1em}(29)} \end{gathered}$$
控制输出
$$y_c(k)=C\Delta x(k)+y_c(k-1),C=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]\text{\hspace{1em}(30)}$$
d轴电流给定为0，给定参考速度为100rad/s，负载转矩0.25Nm，matlab仿真结果如下。稳定时，d轴电流为0，q轴电流为7.3369A，机械角速度为100rad/s。

4 基于MPC的电流环和速度环设计

结合永磁同步电机电气方程和机械方程：
$$\begin{array}{rl}\frac{\mathrm{d}{i}_d}{\mathrm{d}t}=& -\frac{R_s}{L_d}{i}_d+\frac{p_n{\omega }_m{L}_q}{L_d}{i}_q+\frac{u_d}{L_d}\\ \frac{\mathrm{d}{i}_q}{\mathrm{d}t}=& -\frac{p_n{\omega }_m{L}_d}{L_q}{i}_d-\frac{R_s}{L_q}{i}_q+\frac{u_q}{L_q}-\frac{p_n{\omega }_m{\psi }_m}{L_q}\\ \frac{\mathrm{d}{\omega }_m}{\mathrm{d}t}=& \frac{3p_n{\psi }_m}{2J}{i}_q+\frac{3p_n}{2J}(L_d-L_q)i_d{i}_q-\frac{B}{J}{\omega }_m-\frac{T_l}{J}\end{array}\text{\hspace{1em}(31)}$$
这里讨论表贴式永磁同步电机，即$L_d=L_q=L_s$。
$$\begin{array}{rl}\frac{\mathrm{d}{i}_d}{\mathrm{d}t}=& -\frac{R_s}{L_s}{i}_d+p_n{\omega }_m{i}_q+\frac{u_d}{L_s}\\ \frac{\mathrm{d}{i}_q}{\mathrm{d}t}=& -p_n{\omega }_m{i}_d-\frac{R_s}{L_s}{i}_q+\frac{u_q}{L_s}-\frac{p_n{\omega }_m{\psi }_m}{L_s}\\ \frac{\mathrm{d}{\omega }_m}{\mathrm{d}t}=& \frac{3p_n{\psi }_m}{2J}{i}_q-\frac{B}{J}{\omega }_m-\frac{T_l}{J}\end{array}\text{\hspace{1em}(32)}$$
令$x=\left[\begin{array}{ccc}{i}_d& i_q& {\omega }_m\end{array}\right],u=\left[\begin{array}{cc}{u}_d& u_q\end{array}\right]$，则
$$\dot{x}=\left[\begin{array}{ccc}-\frac{R_s}{L_s}& 0& 0\\ 0& -\frac{R_s}{L_s}& -\frac{p_n{\psi }_m}{L_s}\\ 0& \frac{3p_n{\psi }_m}{2J}& -\frac{B}{J}\end{array}\right]x+\left[\begin{array}{cc}-\frac{1}{L_s}& 0\\ 0& -\frac{1}{L_s}\\ 0& 0\end{array}\right]u+\underset{非线性项}{\underbrace{\left[\begin{array}{c}{p}_n{\omega }_m{i}_q\\ -p_n{\omega }_m{i}_d\\ 0\end{array}\right]}}+\left[\begin{array}{c}0\\ 0\\ -\frac{T_l}{J}\end{array}\right]\text{\hspace{1em}(33)}$$
假设$\dot{x}=f(x,u)$，根据全微分方程$\Delta \dot{x}=\frac{\partial f}{\partial x}\Delta x+\frac{\partial f}{\partial u}\Delta u$，将上式线性化：

$$\Delta \dot{x}=\left[\begin{array}{ccc}-\frac{R_s}{L_s}& p_n{\omega }_{m,t}& p_n{i}_{q,t}\\ -p_n{\omega }_{m,t}& -\frac{R_s}{L_s}& -\frac{p_n{\psi }_m}{L_s}-p_n{i}_{d,t}\\ 0& \frac{3p_n{\psi }_m}{2J}& -\frac{B}{J}\end{array}\right]\Delta x+\left[\begin{array}{cc}-\frac{1}{L_s}& 0\\ 0& -\frac{1}{L_s}\\ 0& 0\end{array}\right]\Delta u\text{\hspace{1em}(34)}$$
对式$(34)$离散化得到：
$$\Delta x(k+1)=A\Delta x(k)+B_u\Delta u(k)\text{\hspace{1em}(35)}$$
其中
$$A=\left[\begin{array}{ccc}1-\frac{R_s}{L_s}{T}_s& p_n{\omega }_{m,t}{T}_s& p_n{i}_{q,t}{T}_s\\ -p_n{\omega }_{m,t}{T}_s& 1-\frac{R_s}{L_s}{T}_s& -\frac{p_n{\psi }_m}{L_s}{T}_s-p_n{i}_{d,t}{T}_s\\ 0& \frac{3p_n{\psi }_m}{2J}{T}_s& 1-\frac{B}{J}{T}_s\end{array}\right],B_u=\left[\begin{array}{cc}-\frac{T_s}{L_s}& 0\\ 0& -\frac{T_s}{L_s}\\ 0& 0\end{array}\right]\text{\hspace{1em}(36)}$$
控制输出
$$y_c(k)=C\Delta x(k)+y_c(k-1),C=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]\text{\hspace{1em}(37)}$$
根据第2节中的算法步骤求解，得到控制变量
$$u(k)=\Delta u(k)+u(k-1)\text{\hspace{1em}(38)}$$
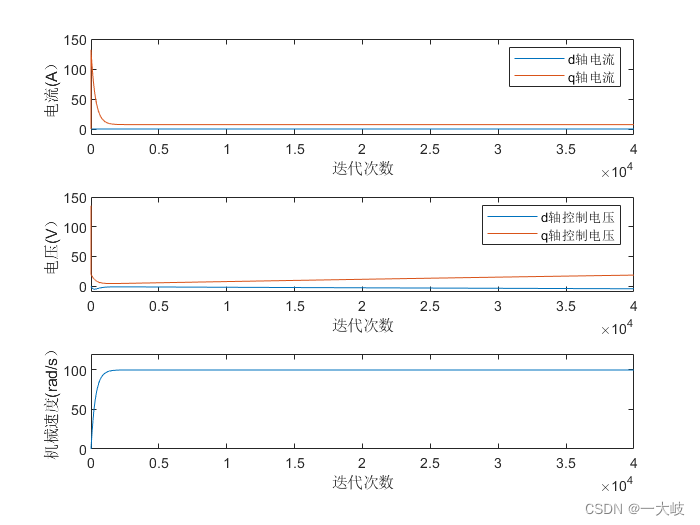
d轴电流给定为0，给定参考速度为100rad/s，负载转矩0.25Nm，matlab仿真结果如下。稳定时，d轴电流为0，q轴电流为7.3366A，机械角速度为99.8453rad/s。

matlab仿真参考代码。

5 参考文献

---

1. 陈虹. 模型预测控制[M]. 北京:科学出版社, 2013. ↩︎