基于蒙特卡洛树搜索的智能驾驶行为规划

最新推荐文章于 2025-03-13 10:18:08 发布

智驾人在路上

最新推荐文章于 2025-03-13 10:18:08 发布

阅读量1.3k

点赞数 34

分类专栏： EPSILON时空联合学习文章标签：自动驾驶动态规划机器学习

本文链接：https://blog.csdn.net/qq_40875526/article/details/142440121

版权

1.蒙特卡洛树搜索的原理

蒙特卡洛树搜索主要分以下四个步骤：选举（selection），扩展（expansion）,模拟（simulation），反向传播（BackPropagation），具体原理见上篇文章蒙特卡洛树搜索算法-CSDN博客

2. 蒙特卡洛树搜索的优势

相比于传统的搜索算法，蒙特卡洛树搜索具有以下优势：

无需事先计算完整的游戏树，避免了组合爆炸的问题
自适应的集中计算资源在有前景的部分游戏树上
通过随机模拟评估每个状态的潜在价值
适用于信息不完全，高维度和大规模的决策问题

3.蒙特卡洛树在智能驾驶中的应用

本文介绍了一种利用基于蒙特卡洛树搜索（MCTS）的算法进行自动驾驶行为规划。该方法的核心目标为利用蒙特卡洛树搜索固有的探索（exploration）和利用（exploitation）之间的平衡来推进复杂场景下的智能决策。

本文引入一种基于MCTS的算法，其适合于自动驾驶的特定需求。这涉及于将精心设计的代价函数（包括安全性，舒适性和可通行性指标）集成到MCTS框架中。该代价函数充当了MCTS算法的引导指南，确保了所生成的决策不仅高效，还与人类驾驶规范相一致。

下图展示了复杂场景中的自动驾驶：无保护左转（图a）和离开高速公路（图b）。在这种具有挑战性的场景下导航需要快速且提前进行决策，以确保安全和舒适的驾驶体验。

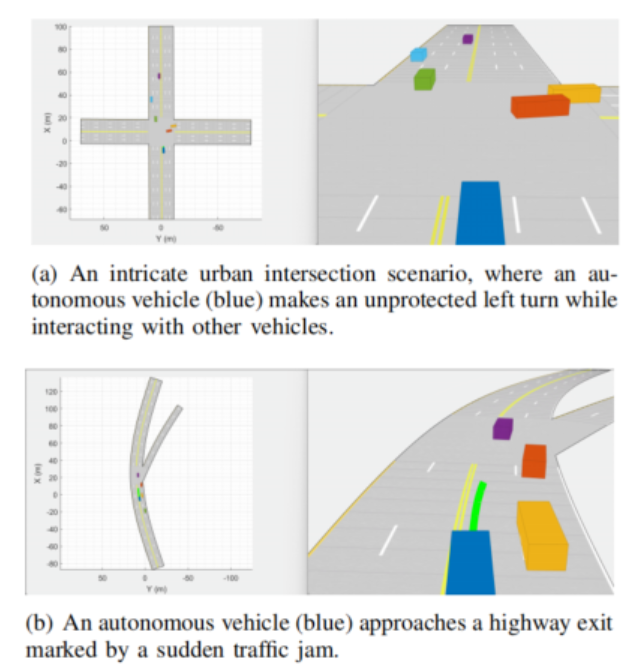
自动驾驶的行为规划问题也可表述为一个优化问题，其优化目标为最小化车辆在给定时间范围内的总体代价。该总体代价由不同的单个代价组成，这些单个代价表征着驾驶的不同方面，对自动驾驶汽车的成功导航至关重要。详细来说，总体代价包括安全性代价、舒适性代价、可通行性代价以及其它可能影响自动驾驶车辆决策过程的因素。

优化问题的目标函数表示为：

J是需要最小化的总体代价， $C_{s}(t)$ 、 $C_{c}(t)$ 、 $C_{p}(t)$ 和 $C_{o}(t)$ 分别指代时刻t的安全性，舒适性，可通行性和其他因素。 $w_{s}$ 、 $w_{c}$ 、 $w_{p}$ 和 $w_{o}$ 分别指代与安全性、舒适性、可通行性和其他因素相关的权重。这些权重决定了目标函数中每一个分量的相对重要性。T为总体时间范围。

行为规划器的目标是确定行为序列，使得目标函数最小化，同时满足所有车辆和环境约束。决策过程必须要遵循若干约束条件，以确保车辆行驶的可行性和安全性。这些约束可分为两大类：

1）车辆运动学约束：这些约束与车辆的物理限制相关，例如最大速度和最小速度、加速度、减速度以及最大偏向角；

2）环境约束：这些约束与车辆和环境的交互相关，例如与其它车辆保持安全距离、维持在车道边界内并且遵守交通规则和信号。

4.蒙特卡洛树搜索伪代码框架

1）首先创建根节点，当根节点的迭代次数与迭代时间没有超过最大的迭代次数或最大的迭代时间时，该算法将会反复迭代，直到达到最终条件。

2）从根节点开始进行行为树的选举，选出UCB值最大的叶节点，如果该叶节点的访问次数为0，则对该节点进行扩展。如果该叶节点的访问次数不为0，则对该节点进行模拟，在模拟过程中，自车的行为是根据给定的运动概率随机生成的，直到达到最终状态。目前，在模拟过程中仅考虑自车的纵向行为（无法变道）。

3）在终止状态下，与自车采取的行为序列相关的总代价是根据上式代价函数来计算获得的。

4）在前向传播达到终止状态且计算完代价后，通过搜索树反向传播该代价。从叶节点开始反向查询到根节点，并且更新前向传播期间遇到的每个节点的累积代价和访问次数。

5.蒙特卡洛树搜索代码解读

（1）首先可根据前向仿真算法预测一段时间内自车与周围车辆的行驶轨迹

（2）树结构的构建与参数的配置

树结构由节点和边组成，其中每个节点表示环境的一个特定状态，每条边表示自车采取的行为。

根节点：根节点表示环境的当前状态，包括局部路线（参考线），自车的状态以及附近其他车辆的状态，代码如下：

TIME = 0;
max_iter = 50; %最大的迭代次数
accMax = 5;  %自车允许的最大加速度
limitJerk = 15; %自车允许的最大加速度的变化率
speedlimit = 20; %自车允许的最大速度
MaxTimeHorizon = 2.0;  %最大的迭代时间
MaxRolloutHorizon = 2.0;  %最大的模拟时间
TimeResolution = 1.0;  %仿真步长
root.visits = 1;  %根节点的访问次数
root.time = TIME; %根节点的访问时间
root.state = startEgoState; % [x y theta kappa speed acc] 自车状态
root.children = 0; %当前子节点的个数
root.index = 1; %节点序号
root.score = 0; %根节点的得分
root.parent = 0; %当前节点的父节点
root.UCB = inf;  %根节点的UCB值
root.egoFrenetState = egoFrenetState;% [s ds dss l dl dll] %自车在Frenet坐标系下的状态
root.laneChangingProperties = struct('LeftChange', 0, 'RightChange', 0, 'Change', false); %换道状态

子节点：子节点通过考虑自车当前状态下可能进行的纵向和横向运动来生成。代码中的子节点主要考虑如下几种：

1）假设自车在做一个突然的减速，给定一个最大为-8的减速度

2）假设自车在匀速运动

3）根据当前自车与参考线的横向偏差，假设自车在匀速向左或向右换道

4）假设自车分别在以-1m/s^2，-2m/s^2，-3m/s^2，-4m/s^2，

-5m/s^2的减速度减速

5）假设自车分别在以1m/s^2，2m/s^2，3m/s^2，4m/s^2，

5m/s^2的加速度加速

（3）树遍历

代码如下：

while (Tree{1}.visits < max_iter) %当根节点的迭代次数小于最大的迭代次数时，反复遍历
        curr_node = selection(Tree{1}, Tree); %选择UCB值最大的节点


        if curr_node.time < MaxTimeHorizon %2
            if numel(curr_node.children) == 1 %当前节点没有子节点
                if curr_node.visits == 0 %当前节点首次被访问
                    % rollout 模拟
                    cost = roll_out(curr_node, MaxRolloutHorizon, TimeResolution, predictedActPositions, accMax, speedlimit, egorefPath, DestinationS, egoVehicle, profiles, scenario);
                    % back propagate 反向传播
                    Tree = back_propagation(curr_node, cost, Tree);
                    Tree = updateUCB(Tree{1}, Tree);
                else
                    % expand 扩展节点
                    Tree = expand(Tree, curr_node, TimeResolution, accMax, speedlimit, egorefPath, predictedActPositions, egoVehicle, profiles, lbdry, roadWidth, scenario);
                    if numel(Tree) == 1
                        Tree{1}.visits = max_iter;
                    end
                end
                curr_node = Tree{1};
            end
        else
            % extra rollout for Maxtimehorizon
            cost = roll_out(curr_node, MaxRolloutHorizon, TimeResolution, predictedActPositions, accMax, speedlimit, egorefPath, DestinationS, egoVehicle, profiles, scenario);
            Tree = back_propagation(curr_node, cost, Tree);
            Tree = updateUCB(Tree{1}, Tree);
            curr_node = Tree{1};
        end
    end

1) 树的选举（selection）

function newNode = selection(node, Tree)
% choose the best node with the biggest UCB score
newNode = Tree{node.index}; %首先让根节点作为新的节点
while numel(newNode.children) ~= 1 %如果当前节点的子节点个数不为1，则开始遍历

    bestChild = Tree{newNode.children(2)};%将第一个子节点作为最优子节点
    for i=2:length(newNode.children) %遍历每一个子节点，选出UCB值最大的子节点
        if Tree{newNode.children(i)}.UCB >= bestChild.UCB
            bestChild = Tree{newNode.children(i)};
        end
    end
    newNode = bestChild;
end
end

2）节点的扩展(expand)

function Tree_ = expand(Tree, node, TimeResolution, accMax, speedlimit, refPath, predicted

最低0.47元/天解锁文章