第二章公式总结
第二章 电磁场的基本规律
电荷守恒定律
电磁场物理模型中的基本物理量可分为源量和场量两大类。
源量为电荷
q
(
r
′
,
t
)
q(r\prime,t)
q(r′,t)和电流
I
(
r
′
,
t
)
I(r\prime,t)
I(r′,t),分别用来描述产生电磁效应的两类场源。电荷是产生电场的源,电流是产生磁场的源。
1.电荷与电荷密度
- 电荷是物质基本属性之一。
- 1897年英国科学家汤姆逊(J.J.Thomson)在实验中发现了电子。
- 1907-1913年间,美国科学家密立根(R.A.Miliken)通过油滴实验,精确测定电子电荷的量值为 e = 1.60217733 × 1 0 − 19 e =1.602 177 33×10^-19 e=1.60217733×10−19(单位:C),确认了电荷量的量子化概念。换句话说,e 是最小的电荷量,而任何带电粒子所带电荷都是e 的整数倍。
- 宏观分析时,电荷常是数以亿计的电子电荷e的组合,故可不考虑其量子化的事实,而认为电荷量q可任意连续取值。
理想化实际带电系统的电荷分布形态分为四种形式:
点电荷、体分布电荷、面分布电荷、线分布电荷
1.电荷体密度

电荷连续分布于体积V内,用电荷体密度来描述其分布
ρ
(
r
⃗
)
=
lim
Δ
V
→
0
Δ
q
(
r
⃗
)
Δ
V
=
d
q
(
r
⃗
)
d
V
\rho(\vec{r})=\lim\limits_{\Delta V\rightarrow 0}\frac{\Delta q(\vec{r})}{\Delta V}=\frac{dq(\vec{r})}{dV}
ρ(r)=ΔV→0limΔVΔq(r)=dVdq(r)单位:C/m3 (库仑/米3 )
根据电荷密度的定义,如果已知某空间区域V中的电荷体密度,则区域V中的总电量q为
q
=
∫
V
ρ
(
r
⃗
)
d
V
q=\int_{V}\rho(\vec{r})dV
q=∫Vρ(r)dV
2.电荷面密度

若电荷分布在薄层上的情况,当仅考虑薄层外,距薄层的距离要比薄层的厚度大得多处的电场,而不分析和计算该薄层内的电场时,可将该薄层的厚度忽略,认为电荷是面分布。面分布的电荷可用电荷面密度表示。
ρ
S
(
r
⃗
)
=
lim
Δ
S
→
0
Δ
q
(
r
⃗
)
Δ
S
=
d
q
(
r
⃗
)
d
S
\rho_S(\vec{r})=\lim\limits_{\Delta S\rightarrow 0}\frac{\Delta q(\vec{r})}{\Delta S}=\frac{dq(\vec{r})}{dS}
ρS(r)=ΔS→0limΔSΔq(r)=dSdq(r)单位: C/m2 (库仑/米2)
如果已知某空间曲面S上的电荷面密度,则该曲面上的总电量q 为
q
=
∫
S
ρ
S
(
r
⃗
)
d
S
q=\int_{S}\rho_S(\vec{r})dS
q=∫SρS(r)dS
3. 电荷线密度

在电荷分布在细线上的情况,当仅考虑细线外,距细线的距离要比细线的直径大得多处的电场,而不分析和计算线内的电场时,可将线的直径忽略,认为电荷是线分布。
ρ
l
(
r
⃗
)
=
lim
Δ
l
→
0
Δ
q
(
r
⃗
)
Δ
l
=
d
q
(
r
⃗
)
d
l
\rho_l(\vec{r})=\lim\limits_{\Delta l\rightarrow 0}\frac{\Delta q(\vec{r})}{\Delta l}=\frac{dq(\vec{r})}{dl}
ρl(r)=Δl→0limΔlΔq(r)=dldq(r)单位: C/m (库仑/米)
如果已知某空间曲线上的电荷线密度,则该曲线上的总电量q 为
q
=
∫
C
ρ
l
(
r
⃗
)
d
l
q=\int_{C}\rho_l(\vec{r})dl
q=∫Cρl(r)dl
4.点电荷

对于总电量为 q 的电荷集中在很小区域 V 的情况,当不分析和计算该电荷所在的小区域中的电场,而仅需要分析和计算电场的区域又距离电荷区很远,即场点距源点的距离远大于电荷所在的源区的线度时,小体积 V 中的电荷可看作位于该区域中心、电量为 q 的点电荷。
点电荷的电荷密度表示
ρ
(
r
⃗
)
=
q
δ
(
r
⃗
−
r
⃗
′
)
\rho(\vec{r})=q\delta(\vec{r}-\vec{r}\prime)
ρ(r)=qδ(r−r′)
位于
r
=
r
′
r=r\prime
r=r′处的点电荷q 的体密度为
q
δ
(
r
⃗
−
r
⃗
′
)
q\delta(\vec{r}-\vec{r}\prime)
qδ(r−r′)
2.电流与电流密度
电流—电荷的定向运动而形成,用i 表示,其大小定义为:单位时间内通过某一横截面S的电荷量,即
i
=
lim
Δ
t
→
0
Δ
q
Δ
t
=
d
q
d
t
i=\lim\limits_{\Delta t\rightarrow 0}\frac{\Delta q}{\Delta t}=\frac{dq}{dt}
i=Δt→0limΔtΔq=dtdq
单位: A (安培)
电流方向: 正电荷的流动方向
形成电流的条件:
- 存在可以自由移动的电荷
- 存在电场
说明:电流通常时时间的函数,不随时间变化的电流称为恒定电流,用
I
I
I表示。
一般情况下,在空间不同的点,电流的大小和方向往往是不同的。在电磁理论中,常用体电流、面电流和线电流来描述电流的分别状态。
1.体电流

电荷在某一体积内定向运动所形成的电流称为体电流,用电流密度矢量
J
⃗
\vec{J}
J来描述。
J
⃗
=
e
⃗
n
lim
Δ
S
→
0
Δ
i
Δ
S
=
e
⃗
n
d
i
d
S
\vec{J}=\vec{e}_n\lim\limits_{\Delta S\rightarrow 0}\frac{\Delta i}{\Delta S}=\vec{e}_n\frac{di}{dS}
J=enΔS→0limΔSΔi=endSdi单位:A/m2 ,
e
⃗
n
\vec{e}_n
en为正电荷运动的方向
流过任意曲面S 的电流为
i
=
∫
S
J
⃗
⋅
d
S
⃗
i=\int_S \vec{J}\cdot d\vec{S}
i=∫SJ⋅dS
2.面电流

电荷在一个厚度可以忽略的薄层内定向运动所形成的电流称为面电流,用面电流密度矢量
J
⃗
S
\vec{J}_S
JS 来描述其分布
J
⃗
S
=
e
⃗
t
lim
Δ
l
→
0
Δ
i
Δ
l
=
e
⃗
t
d
i
d
l
\vec{J}_S=\vec{e}_t\lim\limits_{\Delta l\rightarrow 0}\frac{\Delta i}{\Delta l}=\vec{e}_t\frac{di}{dl}
JS=etΔl→0limΔlΔi=etdldi单位:A/m ,
e
⃗
t
\vec{e}_t
et为正电荷运动的方向
通过薄导体层上任意有向曲线
l
⃗
\vec{l}
l的电流为
i
=
∫
l
J
⃗
S
⋅
(
e
⃗
n
×
d
l
⃗
)
i=\int_l \vec{J}_S\cdot (\vec{e}_n\times d\vec{l})
i=∫lJS⋅(en×dl)
3.电荷守恒定律(电流连续性方程)
- 电荷守恒定律:电荷既不能被创造,也不能被消灭,只能从物体的一部分转移到另一部分,或者从一个物体转移到另一个物体。
- 电荷守恒定律是电磁现象中的基本定律之一。
电流连续性方程
积分形式:
∮
S
J
⃗
⋅
d
S
=
−
d
q
d
t
=
−
d
d
t
∫
V
ρ
d
V
\oint_S \vec{J}\cdot dS=-\frac{dq}{dt}=-\frac{d}{dt}\int_V\rho dV
∮SJ⋅dS=−dtdq=−dtd∫VρdV
(流出闭合面S的电流等于体积V内单位时间所减少的电荷量)
微分形式:
∇
⋅
J
⃗
=
−
∂
ρ
∂
t
\nabla\cdot\vec{J}=-\frac{\partial \rho}{\partial t}
∇⋅J=−∂t∂ρ
恒定电流的连续性方程
∂
ρ
∂
t
=
0
\frac{\partial \rho}{\partial t}=0
∂t∂ρ=0—>
∇
⋅
J
⃗
=
0
,
∮
S
J
⃗
⋅
d
S
=
0
\nabla\cdot\vec{J}=0,\oint_S \vec{J}\cdot dS=0
∇⋅J=0,∮SJ⋅dS=0
恒定电流是无源场,电流是连续的闭合曲面,既起点也无终点。
恒定电流场是一个无散度的场
真空中静电场的基本规律
静电场:由静止电荷产生的电场
重要特征:对位于电场中的电荷有电场力作用
1.库仑定律 电场强度
库仑(Coulomb)定律(1785年)
真空中静止点电荷 q1 对 q2 的作用力:
F
⃗
12
=
e
⃗
R
q
1
q
2
4
π
ε
0
R
12
2
=
q
1
q
2
R
⃗
12
4
π
ε
0
R
12
3
\vec{F}_{12}=\vec{e}_R\frac{q_1q_2}{4\pi\varepsilon_0R^2_{12}}=\frac{q_1q_2\vec{R}_{12}}{4\pi\varepsilon_0R^3_{12}}
F12=eR4πε0R122q1q2=4πε0R123q1q2R12
- 大小与两电荷的电荷量成正比,与两电荷距离的平方成反比;
- 方向沿q1 和q2 连线方向,同性电荷相排斥,异性电荷相吸引;
- F ⃗ 12 = F ⃗ 21 \vec{F}_{12}=\vec{F}_{21} F12=F21 满足牛顿第三定律。
- 电场力服从叠加原理
真空中的N个点电荷 q 1 , q 2 , q 3 . . . q N q_1,q_2,q_3...q_N q1,q2,q3...qN(分别位于 r ⃗ 1 , r ⃗ 2 , r ⃗ 3 . . . r ⃗ N \vec{r}_1,\vec{r}_2,\vec{r}_3...\vec{r}_N r1,r2,r3...rN)对点电荷q(位于 r ⃗ \vec{r} r)的作用力为
F ⃗ q = ∑ i = 1 N F ⃗ q i q = ∑ i = 1 N q q i 4 π ε 0 R I 3 R ⃗ i ( R ⃗ i = r ⃗ − r ⃗ i ) \vec{F}_q=\sum_{i=1}^{N}\vec{F}_{q_iq}=\sum_{i=1}{N}\frac{qq_i}{4\pi\varepsilon_0R^3_I}\vec{R}_i(\vec{R}_i=\vec{r}-\vec{r}_i) Fq=i=1∑NFqiq=i=1∑N4πε0RI3qqiRi(Ri=r−ri)

1.电场强度
电场强度矢量
E
⃗
\vec{E}
E—描述电场分布的基本物理量
空间某点的电场强度定义为置于该点的单位点电荷(又称试验电荷)受到的作用力,即
E
⃗
(
r
⃗
)
=
lim
q
0
→
0
F
⃗
(
r
⃗
)
q
0
\vec{E}(\vec{r})=\lim\limits_{q_0\rightarrow 0}\frac{\vec{F}(\vec{r})}{q_0}
E(r)=q0→0limq0F(r)
q
0
{q_0}
q0—试验正电荷
根据上述定义,真空中静止点电荷q 激发的电场为:
E
⃗
(
r
⃗
)
=
q
R
⃗
4
π
ε
0
R
3
(
R
⃗
=
r
⃗
−
r
⃗
′
)
\vec{E}(\vec{r})=\frac{q\vec{R}}{4\pi\varepsilon_0R^3}(\vec{R}=\vec{r}-\vec{r}\prime)
E(r)=4πε0R3qR(R=r−r′)
体密度为
ρ
(
r
⃗
)
\rho(\vec{r})
ρ(r) 的体分布电荷产生的电场强度,将体电荷公式代入
E
⃗
(
r
⃗
)
=
∑
i
=
1
ρ
(
r
⃗
i
′
)
Δ
V
i
′
R
⃗
i
4
π
ε
0
R
i
3
=
1
4
π
ε
0
∫
V
ρ
(
r
′
⃗
)
R
⃗
R
3
d
V
′
\vec{E}(\vec{r})=\sum_{i=1}\frac{\rho(\vec{r}_i\prime)\Delta V_i\prime \vec{R}_i}{4\pi\varepsilon_0R^3_i}=\frac{1}{4\pi\varepsilon_0}\int_{V}\frac{\rho(\vec{r\prime})\vec{R}}{R^3}dV\prime
E(r)=i=1∑4πε0Ri3ρ(ri′)ΔVi′Ri=4πε01∫VR3ρ(r′)RdV′
面密度为
ρ
S
(
r
⃗
)
\rho_S(\vec{r})
ρS(r)的面分布电荷的电场强度
E
⃗
(
r
⃗
)
=
1
4
π
ε
0
∫
S
ρ
S
(
r
′
⃗
)
R
⃗
R
3
d
S
′
\vec{E}(\vec{r})=\frac{1}{4\pi\varepsilon_0}\int_{S}\frac{\rho_S(\vec{r\prime})\vec{R}}{R^3}dS\prime
E(r)=4πε01∫SR3ρS(r′)RdS′
线密度为
ρ
l
(
r
⃗
)
\rho_l(\vec{r})
ρl(r)的线分布电荷的电场强度
E
⃗
(
r
⃗
)
=
1
4
π
ε
0
∫
C
ρ
l
(
r
′
⃗
)
R
⃗
R
3
d
l
′
\vec{E}(\vec{r})=\frac{1}{4\pi\varepsilon_0}\int_{C}\frac{\rho_l(\vec{r\prime})\vec{R}}{R^3}dl\prime
E(r)=4πε01∫CR3ρl(r′)Rdl′
2. 几种典型电荷分布的电场强度
-
均匀带电直线段的电场强度:

有限长:
E r = ρ l 4 π ε 0 r ( c o s θ 1 − c o s θ 2 ) E_r=\frac{\rho_l}{4\pi\varepsilon_0 r}(cos\theta_1-cos\theta_2) Er=4πε0rρl(cosθ1−cosθ2)
E z = ρ l 4 π ε 0 r ( s i n θ 2 − s i n θ 1 ) E_z=\frac{\rho_l}{4\pi\varepsilon_0 r}(sin\theta_2-sin\theta_1) Ez=4πε0rρl(sinθ2−sinθ1)
无限长:
E ρ = ρ l 2 π ε 0 ρ E_\rho=\frac{\rho_l}{2\pi\varepsilon_0 \rho} Eρ=2πε0ρρl -
均匀带电圆环轴线上的电场强度:
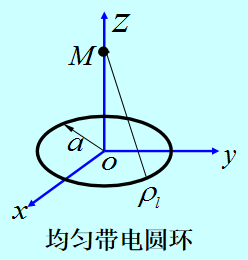
E z ( 0 , 0 , z ) = a ρ l z 2 ε 0 ( a 2 + z 2 ) 3 2 E_z(0,0,z)=\frac{a\rho_lz}{2\varepsilon_0(a^2+z^2)^{\frac{3}{2}}} Ez(0,0,z)=2ε0(a2+z2)23aρlz -
电偶极子的电场强度:

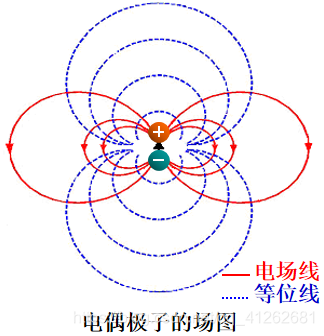
电偶极子是由相距很近、带等值异号的两个点电荷组成的电荷系统,其远区电场强度为
E ⃗ ( r ⃗ ) = 1 4 π ε 0 [ 3 ( p ⃗ ⋅ r ⃗ ) r ⃗ r 5 − p ⃗ r 3 ] = P 4 π ε 0 r 3 ( e ⃗ r 2 c o s θ + e ⃗ θ s i n θ ) \vec{E}(\vec{r})=\frac{1}{4\pi\varepsilon_0}[\frac{3({\vec{p}\cdot\vec{r}})\vec{r}}{r^5}-\frac{\vec{p}}{r^3}]=\frac{P}{4\pi\varepsilon_0r^3}(\vec{e}_r2cos\theta+\vec{e}_\theta sin\theta) E(r)=4πε01[r53(p⋅r)r−r3p]=4πε0r3P(er2cosθ+eθsinθ)
2.静电场的散度与旋度
1.静电场的散度和高斯形式
静电场的散度(微分形式):
∇
⋅
E
⃗
(
r
⃗
)
=
ρ
(
r
⃗
)
ε
0
\nabla\cdot \vec{E}(\vec{r})=\frac{\rho(\vec{r})}{\varepsilon_0}
∇⋅E(r)=ε0ρ(r)(推导见书P43)
静电场的高斯定理(积分形式):
∮
S
E
⃗
(
r
⃗
)
⋅
d
S
⃗
=
1
ε
0
∫
V
ρ
(
r
⃗
)
d
V
\oint_S \vec{E}(\vec{r})\cdot d\vec{S}=\frac{1}{\varepsilon_0}\int_V\rho(\vec{r})dV
∮SE(r)⋅dS=ε01∫Vρ(r)dV
高斯定理表明:静电场是有源场,电场线起始于正电荷,终止于负电荷。
2. 静电场旋度与环路定理
静电场的旋度(微分形式):
∇
×
E
⃗
(
r
⃗
)
=
0
\nabla\times \vec{E}(\vec{r})=0
∇×E(r)=0
静电场的环路定理(积分形式):
∫
c
E
⃗
(
r
⃗
)
⋅
d
l
⃗
=
0
\int_{c}\vec{E}(\vec{r})\cdot d\vec{l}=0
∫cE(r)⋅dl=0
环路定理表明:静电场是无旋场,是保守场,电场力做功和路径无关
3. 利用高斯定理计算电场强度
当电场分布具有一定对称性的情况下,可以利用高斯定理计算电场强度。
具有以下几种对称性的场可用高斯定理求解:
- 球对称分布:包括均匀带电的球面,球体和多层同心球壳等。
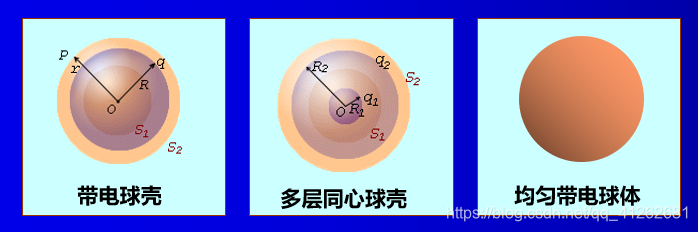
- 轴对称分布:如无限长均匀带电的直线,圆柱面,圆柱壳等。

- 无限大平面电荷:如无限大的均匀带电平面、平板等。

真空中恒定磁场的基本规律
安培力定律 磁感应强度
1. 安培力定律
安培对电流的磁效应进行了大量的实验研究,在 1821~1825年之间,设计并完成了电流相互作用的精巧实验,得到了电流相互作用力公式,称为安培力定律。
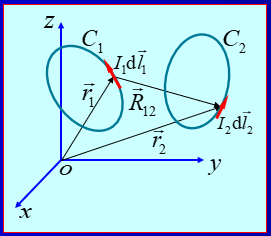
实验表明,真空中的载流回路C1对 载流回路C2的作用力
F
⃗
12
=
μ
0
4
π
∫
C
2
∫
C
1
I
2
d
l
⃗
2
×
(
I
1
d
l
⃗
1
×
R
⃗
12
)
R
12
3
\vec{F}_{12}=\frac{\mu_0}{4\pi}\int_{C_2}\int_{C_1}\frac{I_2d\vec{l}_2\times(I_1d\vec{l}_1\times\vec{R}_{12})}{{R}_{12}^3}
F12=4πμ0∫C2∫C1R123I2dl2×(I1dl1×R12)
载流回路C2对载流回路C1的作用力
F
⃗
21
=
−
F
⃗
12
\vec{F}_{21}=-\vec{F}_{12}
F21=−F12
满足牛顿第三定律
2、磁感应强度 B ⃗ \vec{B} B
电流在其周围空间中产生磁场,描述磁场分布的基本物理量是磁感应强度
B
⃗
\vec{B}
B,单位为T(特斯拉)。
磁场的重要特征是对场中的电流磁场力作
用,载流回路C1对载流回路 C2 的作用力是回路 C1中的电流 I1 产生的磁场对回路 C2中的电流 I2 的作用力。
根据安培力定律,有
F
⃗
12
=
∫
C
2
I
2
d
l
⃗
2
×
μ
0
4
π
∫
C
1
(
I
1
d
l
⃗
1
×
R
⃗
12
)
R
12
3
=
∫
C
2
I
2
d
l
⃗
2
×
B
⃗
1
(
r
⃗
2
)
\vec{F}_{12}=\int_{C_2}I_2d\vec{l}_2\times\frac{\mu_0}{4\pi}\int_{C_1}\frac{(I_1d\vec{l}_1\times\vec{R}_{12})}{{R}_{12}^3}=\int_{C_2}I_2d\vec{l}_2\times\vec{B}_1(\vec{r}_2)
F12=∫C2I2dl2×4πμ0∫C1R123(I1dl1×R12)=∫C2I2dl2×B1(r2)
其中
B
⃗
1
(
r
⃗
2
)
=
μ
0
4
π
∫
C
1
(
I
1
d
l
⃗
1
×
R
⃗
12
)
R
12
3
\vec{B}_1(\vec{r}_2)=\frac{\mu_0}{4\pi}\int_{C_1}\frac{(I_1d\vec{l}_1\times\vec{R}_{12})}{{R}_{12}^3}
B1(r2)=4πμ0∫C1R123(I1dl1×R12)
电流
I
1
I_1
I1在电流元
I
2
d
l
⃗
2
I_2d\vec{l}_2
I2dl2处产生的磁感应强度
任意电流回路C产生的磁场感应强度
B
⃗
(
r
⃗
)
=
μ
0
4
π
∫
C
i
d
l
⃗
′
×
(
r
⃗
−
r
⃗
′
)
∣
r
⃗
−
r
⃗
′
∣
3
=
μ
0
4
π
∫
C
i
d
l
⃗
×
R
⃗
R
3
\vec{B}(\vec{r})=\frac{\mu_0}{4\pi}\int_{C}\frac{id\vec{l}\prime\times(\vec{r}-\vec{r}\prime)}{|\vec{r}-\vec{r}\prime|^3}=\frac{\mu_0}{4\pi}\int_{C}\frac{id\vec{l}\times\vec{R}}{R^3}
B(r)=4πμ0∫C∣r−r′∣3idl′×(r−r′)=4πμ0∫CR3idl×R
电流元
i
d
l
⃗
′
id\vec{l}\prime
idl′产生的磁场感应强度
d
B
⃗
(
r
⃗
)
=
μ
0
4
π
i
d
l
⃗
′
×
(
r
⃗
−
r
⃗
′
)
∣
r
⃗
−
r
⃗
′
∣
3
d\vec{B}(\vec{r})=\frac{\mu_0}{4\pi}\frac{id\vec{l}\prime\times(\vec{r}-\vec{r}\prime)}{|\vec{r}-\vec{r}\prime|^3}
dB(r)=4πμ0∣r−r′∣3idl′×(r−r′)
体电流产生的磁场感应强度
B
⃗
(
r
⃗
)
=
μ
0
4
π
∫
V
J
⃗
(
r
⃗
′
)
×
R
⃗
R
3
d
V
′
\vec{B}(\vec{r})=\frac{\mu_0}{4\pi}\int_{V}\frac{\vec{J}(\vec{r}\prime)\times\vec{R}}{R^3}dV\prime
B(r)=4πμ0∫VR3J(r′)×RdV′
面电流产生的磁感应强度
B
⃗
(
r
⃗
)
=
μ
0
4
π
∫
S
J
⃗
S
(
r
⃗
′
)
×
R
⃗
R
3
d
S
′
\vec{B}(\vec{r})=\frac{\mu_0}{4\pi}\int_{S}\frac{\vec{J}_{S}(\vec{r}\prime)\times\vec{R}}{R^3}dS\prime
B(r)=4πμ0∫SR3JS(r′)×RdS′
3. 几种典型电流分布的磁感应强度
- 载流直线段的磁感应强度:

B ⃗ = e ⃗ ϕ μ 0 I 4 π ρ ( c o s θ 1 − c o s θ 2 ) ( 有 限 长 ) \vec{B}=\vec{e}_\phi\frac{\mu_0 I}{4\pi\rho}(cos\theta_1-cos\theta_2)(有限长) B=eϕ4πρμ0I(cosθ1−cosθ2)(有限长)
B ⃗ = e ⃗ ϕ μ 0 I 2 π ρ ( 无 限 长 ) \vec{B}=\vec{e}_\phi\frac{\mu_0I}{2\pi\rho}(无限长) B=eϕ2πρμ0I(无限长) - 载流圆环轴线上的磁感应强度

B ⃗ ( 0 , 0 , z ) = e ⃗ z μ 0 I a 2 2 ( a 2 + z 2 ) 3 / 2 \vec{B}(0,0,z)=\vec{e}_z\frac{\mu_0I a^2}{2(a^2+z^2)^{3/2}} B(0,0,z)=ez2(a2+z2)3/2μ0Ia2
恒定磁场的散度和旋度
1.恒定磁场的散度和磁通连续性原理
恒定场的散度(微分形式):
∇
⋅
B
⃗
(
r
⃗
)
=
0
\nabla\cdot\vec{B}(\vec{r})=0
∇⋅B(r)=0
磁通连续性原理(积分形式):
∫
S
B
⃗
(
r
⃗
)
⋅
d
S
⃗
=
0
\int_S\vec{B}(\vec{r})\cdot d\vec{S}=0
∫SB(r)⋅dS=0
磁通连续性原理表明:恒定磁场是无源场,磁场线是无起点和终点的闭合曲线
2.恒定磁场的旋度和安培环路定理
恒定磁场的旋度(微分形式):
∇
×
B
⃗
(
r
⃗
)
=
μ
0
J
⃗
(
r
⃗
)
\nabla\times\vec{B}(\vec{r})=\mu_0\vec{J}(\vec{r})
∇×B(r)=μ0J(r)
安培环路定理(积分形式):
∮
C
B
⃗
(
r
⃗
)
⋅
d
l
⃗
=
μ
0
∫
S
J
⃗
(
r
⃗
)
⋅
d
S
⃗
=
μ
0
I
\oint_{C}\vec{B}(\vec{r})\cdot d\vec{l}=\mu_0\int_{S}\vec{J}(\vec{r})\cdot d\vec{S}=\mu_0I
∮CB(r)⋅dl=μ0∫SJ(r)⋅dS=μ0I
安培环路定理表明:恒定磁场是有旋场,是非保守场,电流是磁场的漩涡源
3.利用安培环路定理计算磁感应强度
当磁场分布具有一定对称性的情况下,可以利用安培环路定理计算磁感应强度。
媒质的电磁特性
- 媒质对电磁场的响应可分为三种情况:极化、磁化和传导。
- 描述媒质电磁特性的参数为:介电常数、磁导率和电导率。
电介质的极化 电位移矢量
1.电介质的极化现象

电介质的分子分为无极分子和有极分子。在电场作用下,介质中无极分子的束缚电荷发生位移,有极分子的固有电偶极矩的取向趋于电场方向,这种现象称为电介质的极化。通常,无极分子的极化称为位移极化,有极分子的极化称为取向极化。
2.极化强度矢量 P ⃗ ( C / m 2 ) \vec{P}(C/m^2) P(C/m2)
- 极化强度矢量 是描述介质极化程 度的物理量,定义为
P ⃗ = lim Δ V → 0 ∑ P ⃗ i Δ V = n p ⃗ \vec{P}=\lim\limits_{\Delta V\rightarrow 0}\frac{\sum \vec{P}_i}{\Delta V}=n\vec{p} P=ΔV→0limΔV∑Pi=np
p ⃗ = q l ⃗ − 分 子 的 平 均 电 偶 极 矩 \vec{p}=q\vec{l}-分子的平均电偶极矩 p=ql−分子的平均电偶极矩
- p ⃗ \vec{p} p的物理意义:单位体积内分子电偶极矩的矢量和。
- 极化强度与电场强度有关,其关系一般比较复杂。在线性、 各向同性的电介质中, 与电场强度成正比,即
P ⃗ = x e ε 0 E ⃗ \vec{P}=x_e\varepsilon_0\vec{E} P=xeε0E
x e ( > 0 ) − 电 介 质 的 电 极 化 率 x_e(>0)-电介质的电极化率 xe(>0)−电介质的电极化率
3.极化电荷
由于极化,正负电荷发生位移,在电介质内部可能出现净余的极化电荷分布,同时在电介质的表面上有面分布的极化电荷。
(1)极化电荷体密度

在电介质内任意作一闭合面S,只有电偶极矩穿过S的分子对S内的极化电荷有贡献。由于负电荷位于斜柱体内的电偶极矩才穿过小面元dS,因此dS对极化电荷的贡献为
d
q
p
=
−
q
n
d
d
S
c
o
s
θ
=
−
P
d
S
c
o
s
θ
=
−
P
⃗
⋅
d
S
⃗
dq_p=-qnd dS cos\theta=-PdScos\theta=-\vec{P}\cdot d\vec{S}
dqp=−qnddScosθ=−PdScosθ=−P⋅dS
S所围的体积内的极化电荷
q
p
q_p
qp为
q
p
=
−
∮
S
P
⃗
⋅
d
S
⃗
=
−
∫
V
∇
⋅
P
⃗
d
V
q_p=-\oint_S \vec{P}\cdot d\vec{S}=-\int_V \nabla\cdot \vec{P}dV
qp=−∮SP⋅dS=−∫V∇⋅PdV
ρ
p
=
−
∇
⋅
P
⃗
\rho_p=-\nabla\cdot \vec{P}
ρp=−∇⋅P
(2)极化电荷面密度
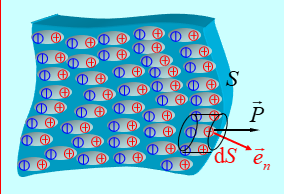
紧贴电介质表面取如图所示的闭曲面,则穿过面积元的极化电荷为
d
q
p
=
q
n
d
d
S
c
o
s
θ
=
P
d
S
c
o
s
θ
=
P
⃗
⋅
d
S
⃗
dq_p=qnd dS cos\theta=PdScos\theta=\vec{P}\cdot d\vec{S}
dqp=qnddScosθ=PdScosθ=P⋅dS
故得到电介质表面的极化电荷面密度为
ρ
S
P
=
P
⃗
e
⃗
n
\rho_{SP}=\vec{P}\vec{e}_n
ρSP=Pen
4. 电位移矢量 介质中的高斯定理
介质的极化过程包括两个方面:
- 外加电场的作用使介质极化,产生极化电荷;
- 极化电荷反过来激发电场,两者相互制约,并达到平衡状 态。无论是自由电荷,还是极化电荷,它们都激发电场,服从同样的库仑定律和高斯定理。
介质中的电场应该是外加电场和极化电荷产生的电场的叠加,应用高斯定理得到:
∮
S
E
⃗
⋅
d
S
⃗
=
1
ε
0
∫
V
(
ρ
+
ρ
0
)
d
V
\oint_S\vec{E}\cdot d\vec{S}=\frac{1}{\varepsilon_0}\int_V(\rho+\rho_0)dV
∮SE⋅dS=ε01∫V(ρ+ρ0)dV
ε
0
∇
⋅
E
⃗
=
ρ
+
ρ
p
\varepsilon_0\nabla\cdot \vec{E}=\rho+\rho_p
ε0∇⋅E=ρ+ρp
将极化电荷体密度表达式
ρ
p
=
−
∇
⋅
P
⃗
\rho_p=-\nabla\cdot \vec{P}
ρp=−∇⋅P
代入
ε
0
∇
⋅
E
⃗
=
ρ
+
ρ
p
\varepsilon_0\nabla\cdot \vec{E}=\rho+\rho_p
ε0∇⋅E=ρ+ρp,有
ε
0
∇
⋅
E
⃗
=
ρ
−
∇
⋅
P
⃗
\varepsilon_0\nabla\cdot \vec{E}=\rho-\nabla\cdot \vec{P}
ε0∇⋅E=ρ−∇⋅P
引入电位移矢量(单位为
C
/
m
2
C/m^2
C/m2)
D
⃗
=
ε
0
E
⃗
+
P
⃗
\vec{D}=\varepsilon_0\vec{E}+\vec{P}
D=ε0E+P
则有
∇
⋅
D
⃗
=
ρ
\nabla \cdot \vec{D}=\rho
∇⋅D=ρ
其积分形式为
∮
S
D
⃗
⋅
d
S
⃗
=
∫
V
ρ
d
V
\oint_S\vec{D}\cdot d\vec{S}=\int_V\rho dV
∮SD⋅dS=∫VρdV(任意闭合曲面电位移矢量 D 的通量等于该曲面包含自由电荷的代数和 )
小结:静电场是有源无旋场,电介质中的基本方程为
{
∇
⋅
D
⃗
=
ρ
∇
×
E
⃗
=
0
(
微
分
形
式
)
\begin{cases} {\nabla\cdot \vec{D}=\rho}\\ {\nabla\times\vec{E}=0} \end{cases}(微分形式)
{∇⋅D=ρ∇×E=0(微分形式)
{ ∫ S D ⃗ ⋅ d S ⃗ = ∫ V ρ d V ∫ C E ⃗ ( r ⃗ ) ⋅ d l ⃗ = 0 ( 积 分 形 式 ) \begin{cases} {\int_S\vec{D}\cdot d\vec{S}=\int_V\rho dV}\\ {\int_C \vec{E}(\vec{r})\cdot d\vec{l}=0} \end{cases}(积分形式) {∫SD⋅dS=∫VρdV∫CE(r)⋅dl=0(积分形式)
5.电介质的本构关系
极化强度
P
⃗
\vec{P}
P和电场强度
E
⃗
\vec{E}
E的之间的关系由介质的性质决定。对于线性各向同性介质,
P
⃗
\vec{P}
P和
E
⃗
\vec{E}
E有简单的线性关系
P
⃗
=
ε
0
x
e
E
⃗
\vec{P}=\varepsilon_0x_e\vec{E}
P=ε0xeE
在这种情况下由
D
⃗
=
ε
0
(
1
+
x
e
)
E
⃗
=
ε
E
⃗
=
ε
r
ε
0
E
⃗
\vec{D}=\varepsilon_0(1+x_e)\vec{E}=\varepsilon\vec{E}=\varepsilon_r\varepsilon_0\vec{E}
D=ε0(1+xe)E=εE=εrε0E
其中
ε
=
ε
0
(
1
+
x
e
)
=
ε
r
ε
0
\varepsilon=\varepsilon_0(1+x_e)=\varepsilon_r\varepsilon_0
ε=ε0(1+xe)=εrε0称为介质的介电常数,
ε
r
=
1
+
x
e
\varepsilon_r=1+x_e
εr=1+xe称为介质的相对介电常数(无量纲)。
磁介质的磁化 磁场强度
1.磁介质的磁化
介质中的分子或原子内的电子运动形成分子电流,形成分子磁矩

P
⃗
m
=
i
Δ
S
⃗
\vec{P}_m=i\Delta\vec{S}
Pm=iΔS
无外磁场作用时,分子磁矩不规则排列,宏观上不显磁性。

在外磁场作用下,分子磁矩定向排列,宏观上显示出磁性,这种现象称为磁介质的磁化。
2. 磁化强度矢量 M ⃗ \vec{M} M
磁化强度
M
⃗
\vec{M}
M是描述磁介质磁化程度的物理量,定义为单位体积中的分子磁矩的矢量和,即
M
⃗
=
lim
Δ
V
→
0
∑
P
⃗
m
Δ
V
=
n
p
⃗
m
\vec{M}=\lim\limits_{\Delta V\rightarrow 0}\frac{\sum \vec{P}_m}{\Delta V}=n\vec{p}_m
M=ΔV→0limΔV∑Pm=npm
单位为A/m
3. 磁化电流

磁介质被磁化后,在其内部与表面上可能出现宏观的电流分布,称为磁化电流。
(1)磁化电流体密度
J
⃗
M
\vec{J}_M
JM
考察穿过任意围线C所围曲面S的电流。只有分子电流与围线相交链的分子才对电流有贡献。与线元dl相交链的分子,中心位于如图所示的斜圆柱内,所交链的电流
d
I
M
=
n
i
Δ
S
⃗
⋅
d
l
⃗
=
n
p
⃗
m
⋅
d
l
⃗
=
M
⃗
⋅
d
l
⃗
dI_M=ni\Delta\vec{S}\cdot d\vec{l}=n\vec{p}_m\cdot d\vec{l}=\vec{M}\cdot d\vec{l}
dIM=niΔS⋅dl=npm⋅dl=M⋅dl
穿过曲面S的磁化电流为
I
M
=
∫
C
d
I
M
=
∫
C
M
⃗
⋅
d
l
⃗
=
∫
S
∇
×
M
⃗
⋅
d
S
⃗
I_M=\int_CdI_M=\int_C\vec{M}\cdot d\vec{l}=\int_S \nabla\times\vec{M}\cdot d\vec{S}
IM=∫CdIM=∫CM⋅dl=∫S∇×M⋅dS
由
I
M
=
∫
S
J
⃗
M
I_M=\int_S{\vec{J}_M}
IM=∫SJM即得到磁化电流体密度
J
⃗
M
=
∇
×
M
⃗
\vec{J}_M=\nabla\times\vec{M}
JM=∇×M
(2)磁化电流面密度
J
⃗
S
M
\vec{J}_{SM}
JSM
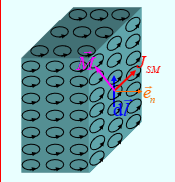
在紧贴磁介质表面取一长度源dl,在此交链的磁化电流为
d
I
M
=
M
⃗
⋅
l
⃗
=
M
⃗
⋅
e
⃗
t
d
l
=
M
t
d
l
dI_M=\vec{M}\cdot\vec{l}=\vec{M}\cdot\vec{e}_tdl=M_tdl
dIM=M⋅l=M⋅etdl=Mtdl
则
J
⃗
S
M
=
M
t
\vec{J}_{SM}=M_t
JSM=Mt
即
J
⃗
S
M
=
M
⃗
×
e
⃗
n
\vec{J}_{SM}=\vec{M}\times\vec{e}_n
JSM=M×en
4. 磁场强度 介质中安培环路定理
外加磁场使得介质发生磁化,磁化导致磁化电流。磁化电流同样也激发磁感应强度,两种相互作用达到平衡介质中的磁感应强度B 应是所有电流源激励的结果:
∇
×
B
⃗
=
μ
0
(
J
⃗
+
J
⃗
M
)
\nabla \times \vec{B}=\mu_0(\vec{J}+\vec{J}_M)
∇×B=μ0(J+JM)
∮
C
B
⃗
⋅
d
l
⃗
=
μ
0
∫
S
(
J
⃗
+
J
⃗
M
)
⋅
d
S
⃗
\oint_C \vec{B}\cdot d\vec{l}=\mu_0\int_S(\vec{J}+\vec{J}_M)\cdot d\vec{S}
∮CB⋅dl=μ0∫S(J+JM)⋅dS
J
⃗
和
J
⃗
M
\vec{J}和\vec{J}_M
J和JM分别是传导电流密度和磁化电流密度
将极化电荷体密度表达式
J
⃗
M
=
∇
×
M
⃗
\vec{J}_M=\nabla\times \vec{M}
JM=∇×M代入
∇
×
B
⃗
=
μ
0
(
J
⃗
+
J
⃗
M
)
\nabla \times \vec{B}=\mu_0(\vec{J}+\vec{J}_M)
∇×B=μ0(J+JM)
有
∇
×
(
B
⃗
μ
0
−
M
⃗
)
=
J
⃗
\nabla \times (\frac{\vec{B}}{\mu_0}-\vec{M})=\vec{J}
∇×(μ0B−M)=J
定义磁场强度
H
⃗
\vec{H}
H为:
H
⃗
=
B
⃗
μ
0
−
M
⃗
\vec{H}=\frac{\vec{B}}{\mu_0}-\vec{M}
H=μ0B−M,即
B
⃗
=
μ
0
(
H
⃗
+
M
⃗
)
\vec{B}=\mu_0(\vec{H}+\vec{M})
B=μ0(H+M)
则得到介质中的安培环路定理为:
∮
C
H
⃗
(
r
⃗
)
⋅
d
l
⃗
=
∫
S
J
⃗
(
r
⃗
)
⋅
d
S
⃗
\oint_C\vec{H}(\vec{r})\cdot d\vec{l}=\int_S \vec{J}(\vec{r})\cdot d\vec{S}
∮CH(r)⋅dl=∫SJ(r)⋅dS
∇
×
H
⃗
(
r
⃗
)
=
J
⃗
(
r
⃗
)
\nabla\times\vec{H}(\vec{r})=\vec{J}(\vec{r})
∇×H(r)=J(r)
磁通连续性定理为
∮
S
B
⃗
(
r
⃗
)
⋅
d
S
⃗
=
0
\oint_S\vec{B}(\vec{r})\cdot d\vec{S}=0
∮SB(r)⋅dS=0
∇
⋅
B
⃗
(
r
⃗
)
=
0
\nabla\cdot \vec{B}(\vec{r})=0
∇⋅B(r)=0
小结:恒定磁场是有源无旋场,磁介质中的基本方程为
{
∇
×
H
⃗
(
r
⃗
)
=
J
⃗
(
r
⃗
)
∇
⋅
B
⃗
(
r
⃗
)
=
0
(
微
分
形
式
)
\begin{cases} {\nabla\times\vec{H}(\vec{r})=\vec{J}(\vec{r})}\\{\nabla\cdot \vec{B}(\vec{r})=0} \end{cases}(微分形式)
{∇×H(r)=J(r)∇⋅B(r)=0(微分形式)
{
∮
C
H
⃗
(
r
⃗
)
⋅
d
l
⃗
=
∫
S
J
⃗
(
r
⃗
)
⋅
d
S
⃗
∮
S
B
(
r
⃗
)
⋅
d
S
⃗
=
0
⃗
(
积
分
形
式
)
\begin{cases} {\oint_C\vec{H}(\vec{r})\cdot d\vec{l}=\int_S\vec{J}(\vec{r})\cdot d\vec{S}}\\{\oint_S\vec{B(\vec{r})\cdot d\vec{S}=0}} \end{cases}(积分形式)
{∮CH(r)⋅dl=∫SJ(r)⋅dS∮SB(r)⋅dS=0(积分形式)
5. 磁介质的本构关系
磁化强度
M
⃗
\vec{M}
M与磁场强度
H
⃗
\vec{H}
H之间的关系由介质的性质决定。对于线性各向同性介质,
M
⃗
\vec{M}
M 和
H
⃗
\vec{H}
H有简单的线性关系
M
⃗
=
x
m
H
⃗
\vec{M}=x_m\vec{H}
M=xmH
其中,
x
m
x_m
xm称为介质的磁化率(也成为磁化系数)。
这种情况下
B
⃗
=
μ
0
(
1
+
x
m
)
H
⃗
=
μ
H
⃗
\vec{B}=\mu_0(1+x_m)\vec{H}=\mu\vec{H}
B=μ0(1+xm)H=μH
其中
μ
=
μ
0
(
1
+
x
m
)
=
μ
r
μ
0
\mu=\mu_0(1+x_m)=\mu_r\mu_0
μ=μ0(1+xm)=μrμ0称为介质的磁导率,
μ
r
=
1
+
x
m
\mu_r=1+x_m
μr=1+xm称为介质的相对磁导率(无量纲)
磁介质的分类
μ
r
>
1
\mu_r>1
μr>1顺磁质
μ
r
<
1
\mu_r<1
μr<1抗磁质
μ
r
>
>
1
\mu_r>>1
μr>>1铁磁质
媒质的传导特性
1.定义 存在可以自由移动带电粒子的介质称为导电媒质。在外场作用下,导电媒质中将形成定向移动电流。

2,公式 对于线性和各向同性导电媒质,媒质内任一点的电流密度矢量 J 和电场强度 E 成正比,表示为
J
⃗
=
σ
E
⃗
\vec{J}=\sigma\vec{E}
J=σE
这就是欧姆定律的微分形式。式中的比例系数
σ
\sigma
σ称为媒质的电导率,单位是S/m(西门子/米)。
电磁感应定律和位移电流
- 电磁感应定律 —— 揭示时变磁场产生电场
- 位移电流 —— 揭示时变电场产生磁场
- 重要结论: 在时变情况下,电场与磁场相互激励,形成统一 的电磁场。
电磁感应定律
自从1820年奥斯特发现电流的磁效应之后,人们开始研究相反的问题,即磁场能否产生电流。
1881年法拉弟发现,当穿过导体回路的磁通量发生变化时,回路中就会出现感应电流和电动势,且感应电动势与磁通量的变化有密切关系,由此总结出了著明的法拉电磁感应定律。
1 法拉弟电磁感应定律的表述
当通过导体回路所围面积的磁通量 发生变化时,回路中产生的感应电动势
ε
i
n
\varepsilon_{in}
εin的大小等于磁通量的时间变化率的负值,方向是要阻止回路中磁通量的改变,即
ε
i
n
=
−
d
ψ
d
t
\varepsilon_{in}=-\frac{d \psi}{dt}
εin=−dtdψ
负号表示感应电流产生的磁场总是阻止磁通量的变化。
设任意导体回路C围成的曲面为
S
′
S\prime
S′,其单位法向矢量为
e
⃗
n
\vec{e}_n
en,则穿过回路的磁通为
ψ
=
∫
S
B
⃗
⋅
d
S
⃗
\psi=\int_S \vec{B}\cdot d\vec{S}
ψ=∫SB⋅dS
ε
i
n
=
−
d
d
t
∫
S
B
⃗
⋅
d
S
⃗
\varepsilon_{in}=-\frac{d}{dt}\int_S\vec{B}\cdot d\vec{S}
εin=−dtd∫SB⋅dS
导体回路中有感应电流,表明回路中存在感应电场 ,回路中的感应电动势可表示为
ε
i
n
=
∫
C
E
⃗
m
⋅
d
l
⃗
\varepsilon_{in}=\int_C\vec{E}_m\cdot d\vec{l}
εin=∫CEm⋅dl
因而有
∫
C
E
⃗
m
⋅
d
l
⃗
=
−
d
d
t
∫
S
B
⃗
⋅
d
S
⃗
\int_C\vec{E}_m\cdot d\vec{l}=-\frac{d}{dt}\int_S \vec{B}\cdot d\vec{S}
∫CEm⋅dl=−dtd∫SB⋅dS
对感应电场的讨论:
- 感应电场是由变化的磁场所激发的电场;
- 感应电场是有旋场;
- 感应电场不仅存在于导体回路中,也存在于导体回路之外的
空间; - 对空间中的任意回路(不一定是导体回路)C ,都有
∫ C E ⃗ m ⋅ d l ⃗ = − d d t ∫ S B ⃗ ⋅ d S ⃗ \int_C\vec{E}_m\cdot d\vec{l}=-\frac{d}{dt}\int_S\vec{B}\cdot d\vec{S} ∫CEm⋅dl=−dtd∫SB⋅dS
若空间同时存在由电荷产生的电场,则总电场 E ⃗ \vec{E} E应为 E ⃗ m \vec{E}_m Em与 E ⃗ c \vec{E}_c Ec之和。由于 E ⃗ = E ⃗ m + E ⃗ c \vec{E}=\vec{E}_m+\vec{E}_c E=Em+Ec,故有 ∫ C E ⃗ c ⋅ d l ⃗ = 0 \int_C\vec{E}_c\cdot d\vec{l}=0 ∫CEc⋅dl=0
∫
C
E
⃗
⋅
d
l
⃗
=
−
d
d
t
∫
S
B
⃗
⋅
d
S
⃗
\int_C\vec{E}\cdot d\vec{l}=-\frac{d}{dt}\int_S\vec{B}\cdot d\vec{S}
∫CE⋅dl=−dtd∫SB⋅dS
这就是推广的法拉第电磁感应定律
2.引起回路中磁通变化的几种情况:
(1)回路不变,磁场随时间变化
磁通量的变化由磁场随时间变化引起,因此有
d
d
t
∫
S
B
⃗
⋅
d
S
⃗
=
∫
S
∂
B
⃗
∂
t
⋅
d
S
⃗
\frac{d}{dt}\int_S\vec{B}\cdot d\vec{S}=\int_S\frac{\partial \vec{B}}{\partial t}\cdot d\vec{S}
dtd∫SB⋅dS=∫S∂t∂B⋅dS
∫
C
E
⃗
⋅
d
l
⃗
=
−
∫
S
∂
B
⃗
∂
t
⋅
d
S
⃗
\int_C\vec{E}\cdot d\vec{l}=-\int_S\frac{\partial \vec{B}}{\partial t}\cdot d\vec{S}
∫CE⋅dl=−∫S∂t∂B⋅dS
相应的微分形式为
∇
×
E
⃗
=
−
∂
B
⃗
∂
t
\nabla \times \vec{E}=-\frac{\partial \vec{B}}{\partial t}
∇×E=−∂t∂B
(2)导体回路在恒定磁场中运动
ε
i
n
=
∫
C
E
⃗
⋅
d
l
⃗
=
∫
C
(
v
⃗
×
B
⃗
)
⋅
d
l
⃗
\varepsilon_{in}=\int_C\vec{E}\cdot d\vec{l}=\int_C(\vec{v}\times\vec{B})\cdot d\vec{l}
εin=∫CE⋅dl=∫C(v×B)⋅dl
称为动生电动势,这就是
E
=
F
m
/
q
=
∫
C
q
v
⃗
×
B
⃗
/
q
⋅
d
l
⃗
=
∫
C
(
v
⃗
×
B
⃗
)
⋅
d
l
⃗
E=F_m/q=\int_Cq\vec{v}\times\vec{B}/q\cdot d\vec{l}=\int_C(\vec{v}\times\vec{B})\cdot d\vec{l}
E=Fm/q=∫Cqv×B/q⋅dl=∫C(v×B)⋅dl
(3)回路在时变磁场中运动
ε
i
n
=
∫
C
E
⃗
⋅
d
l
⃗
=
∫
C
(
v
⃗
×
B
⃗
)
⋅
d
l
⃗
−
∫
S
∂
B
⃗
∂
t
⋅
d
S
⃗
\varepsilon_{in}=\int_C\vec{E}\cdot d\vec{l}=\int_C(\vec{v}\times\vec{B})\cdot d\vec{l}-\int_S\frac{\partial \vec{B}}{\partial t}\cdot d\vec{S}
εin=∫CE⋅dl=∫C(v×B)⋅dl−∫S∂t∂B⋅dS
位移电流
静态情况下的电场基本方程在非静态时发生了变化,即
∇
×
E
⃗
=
0
\nabla \times \vec{E}=0
∇×E=0
变成
∇
×
E
⃗
=
−
∂
B
⃗
∂
t
\nabla \times \vec{E}=-\frac{\partial \vec{B}}{\partial t}
∇×E=−∂t∂B
这不仅是方程形式的变化,而是一个本质的变化,其中包含了重要的物理事实,即 时变磁场可以激发电场 。
1.全电流定律
∇
×
H
⃗
=
J
⃗
+
∂
D
⃗
∂
t
−
微
分
形
式
\nabla \times \vec{H}=\vec{J}+\frac{\partial \vec{D}}{\partial t}-微分形式
∇×H=J+∂t∂D−微分形式
∮
C
H
⃗
⋅
d
l
⃗
=
∫
S
(
J
⃗
+
∂
D
⃗
∂
t
)
⋅
d
S
⃗
−
积
分
形
式
\oint_C\vec{H}\cdot d\vec{l}=\int_S(\vec{J}+\frac{\partial \vec{D}}{\partial t})\cdot d\vec{S}-积分形式
∮CH⋅dl=∫S(J+∂t∂D)⋅dS−积分形式
全电流定律揭示不仅传导电流激发磁场,变化的电场也可以激发磁场。它与变化的磁场激发电场形成自然界的一个对偶关系
2.位移电流密度

J ⃗ d = ∂ D ⃗ ∂ t \vec{J}_d=\frac{\partial \vec{D}}{\partial t} Jd=∂t∂D
-
电位移矢量随时间的变化率,能像电流一样产生磁场,故称“位移电流”。
-
位移电流只表示电场的变化率,与传导电流不同,它不产生热效应。
-
位移电流的引入是建立麦克斯韦方程组的至关重要的一步,它揭示了时变电场产生磁场这一重要的物理概念。
注:
在绝缘介质中,无传导电流,但有位移电流; 在理想导体中,无位移电流,但有传导电流; 在一般介质中,既有传导电流,又有位移电流。
麦克斯韦方程
麦克斯韦方程组-宏观电磁现象所遵循的基本规律,是电磁场的基本现象
1.麦克斯韦方程组的积分形式
{
∫
C
H
⃗
⋅
d
l
⃗
=
∫
S
(
J
⃗
+
∂
D
⃗
∂
t
)
⋅
d
S
⃗
∫
C
E
⃗
⋅
d
l
⃗
=
−
∫
S
∂
B
⃗
∂
t
⋅
d
S
⃗
∫
S
B
⃗
⋅
d
S
⃗
=
0
∫
S
D
⃗
⋅
d
S
⃗
=
−
∫
V
ρ
d
V
\begin{cases} {\int_C\vec{H}\cdot d\vec{l}=\int_S(\vec{J}+\frac{\partial \vec{D}}{\partial t})\cdot d\vec{S}}\\{\int_C\vec{E}\cdot d\vec{l}=-\int_S\frac{\partial \vec{B}}{\partial t}\cdot d\vec{S}}\\{\int_S\vec{B}\cdot d\vec{S}=0}\\{\int_S\vec{D}\cdot d\vec{S}=-\int_V\rho d V} \end{cases}
⎩⎪⎪⎪⎨⎪⎪⎪⎧∫CH⋅dl=∫S(J+∂t∂D)⋅dS∫CE⋅dl=−∫S∂t∂B⋅dS∫SB⋅dS=0∫SD⋅dS=−∫VρdV
∮
S
J
⃗
⋅
d
S
⃗
=
−
∫
V
ρ
d
V
\oint_S\vec{J}\cdot d\vec{S}=-\int_V\rho dV
∮SJ⋅dS=−∫VρdV
2.麦克斯韦方程组的微分形式
{
∇
×
H
⃗
=
J
⃗
+
∂
D
⃗
∂
t
∇
E
⃗
=
−
∂
B
⃗
∂
t
∇
⋅
B
⃗
=
0
∇
⋅
D
⃗
=
ρ
\begin{cases} {\nabla \times \vec{H}=\vec{J}+\frac{\partial \vec{D}}{\partial t}}\\{\nabla \vec{E}=-\frac{\partial \vec{B}}{\partial t}}\\{\nabla \cdot \vec{B}=0}\\{\nabla\cdot\vec{D}=\rho} \end{cases}
⎩⎪⎪⎪⎨⎪⎪⎪⎧∇×H=J+∂t∂D∇E=−∂t∂B∇⋅B=0∇⋅D=ρ
麦克斯韦第一方程,表明传导电流和变化的电场都能产生磁场
麦克斯韦第二方程,表明变化的磁场产生电场
麦克斯韦第三方程表明磁场是无源场,磁力线总是闭合曲线
麦克斯韦第四方程,表明电荷产生电场
3.媒质的本构关系
各项同性线性媒质的本构关系为
D
⃗
=
ε
E
⃗
\vec{D}=\varepsilon\vec{E}
D=εE
B
⃗
=
μ
H
⃗
\vec{B}=\mu\vec{H}
B=μH
J
⃗
=
σ
E
⃗
\vec{J}=\sigma\vec{E}
J=σE
代入到麦克斯韦方程组中,有

均匀媒质


时变电场的激发源除了电荷以外,还有变化的磁场;而时变磁场的激发源除了传导电流以外,还有变化的电场。电场和磁场互为激发源,相互激发。
时变电磁场的电场和磁场不再相互独立,而是相互关联,构成一个整体 —— 电磁场。电场和磁场分别是电磁场的两个分量。
在离开辐射源(如天线)的无源空间中,电荷密度和电流密度矢量为零,电场和磁场仍然可以相互激发,从而在空间形成电磁振荡并传播,这就是电磁波。
在无源空间中,两个旋度方程分别为
∇
×
H
⃗
=
∂
D
⃗
∂
t
\nabla\times\vec{H}=\frac{\partial \vec{D}}{\partial t}
∇×H=∂t∂D
∇
×
E
⃗
=
−
∂
B
⃗
∂
t
\nabla\times\vec{E}=-\frac{\partial \vec{B}}{\partial t}
∇×E=−∂t∂B
可以看到两个方程的右边相差一个负号,而正是这个负号使得电场和磁场构成一个相互激励又相互制约的关系。当磁场减小时,电场的漩涡源为正,电场将增大;而当电场增大时,使磁场增大,磁场增大反过来又使电场减小。

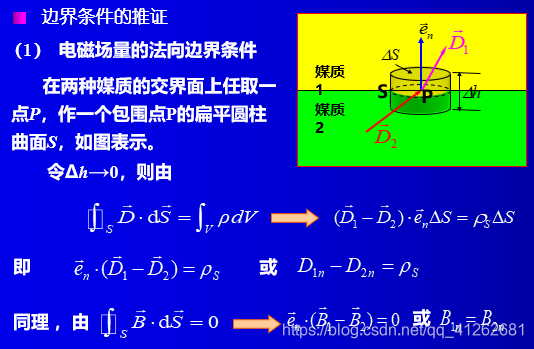
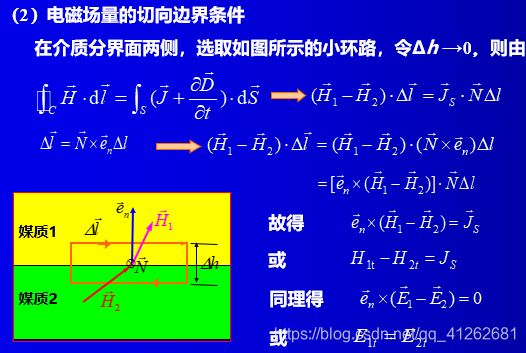
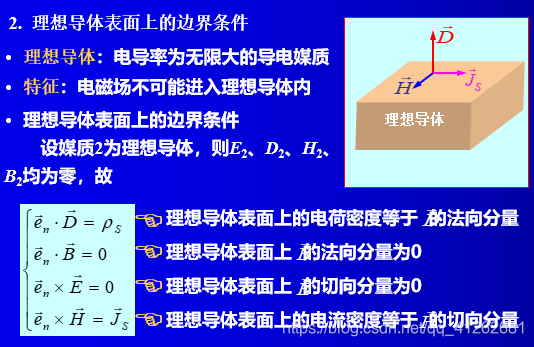
电磁场的边界条件

实际电磁场问题都是在一定的物理空间内发生的,该空间中可能是由多种不同媒质组成的。边界条件就是不同媒质的分界面上的电磁场矢量满足的关系,是在不同媒质分界面上电磁场的基本属性。
物理:由于在分界面两侧介质的特性参数发生突变,场在界面两侧也发生突变。麦克斯韦方程组的微分形式在分界面两侧失去意义,必须采用边界条件。
数学:麦克斯韦方程组是微分方程组,其解是不确定的,边界条件起定解的作用。
麦克斯韦方程组的积分形式在不同媒质的分界面上仍然适用,由此可导出电磁场矢量在不同媒质分界面上的边界条件。

























 16万+
16万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








