机器学习入门（三）多元线性回归

最新推荐文章于 2023-03-22 15:33:00 发布

APS2023

最新推荐文章于 2023-03-22 15:33:00 发布

阅读量1.5k

点赞数 3

分类专栏：机器学习文章标签：机器学习线性回归

本文链接：https://blog.csdn.net/qq_41694024/article/details/127611957

版权

机器学习专栏收录该内容

8 篇文章 9 订阅

订阅专栏

3.4.2 多元线性回归梯度下降算法的问题

3.多元线性回归

3.1 前提回顾

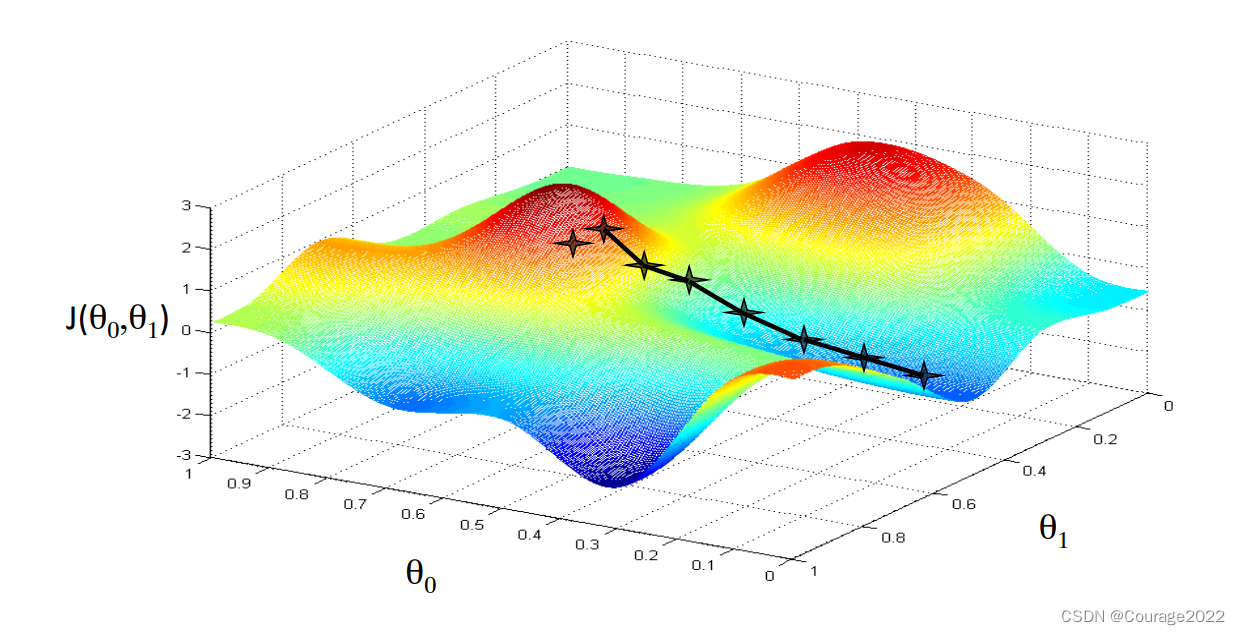
我们在上一章提出了一元线性回归，我们首先提出了一元线性回归的假设方程，随后我们介绍了它的代价方程。计算机系统能绘制不同的参数对应的代价，如下图。

然后我们想找一个最低点，这时引入了梯度下降法和下降因子。我们最后得到了一个局部最低点。

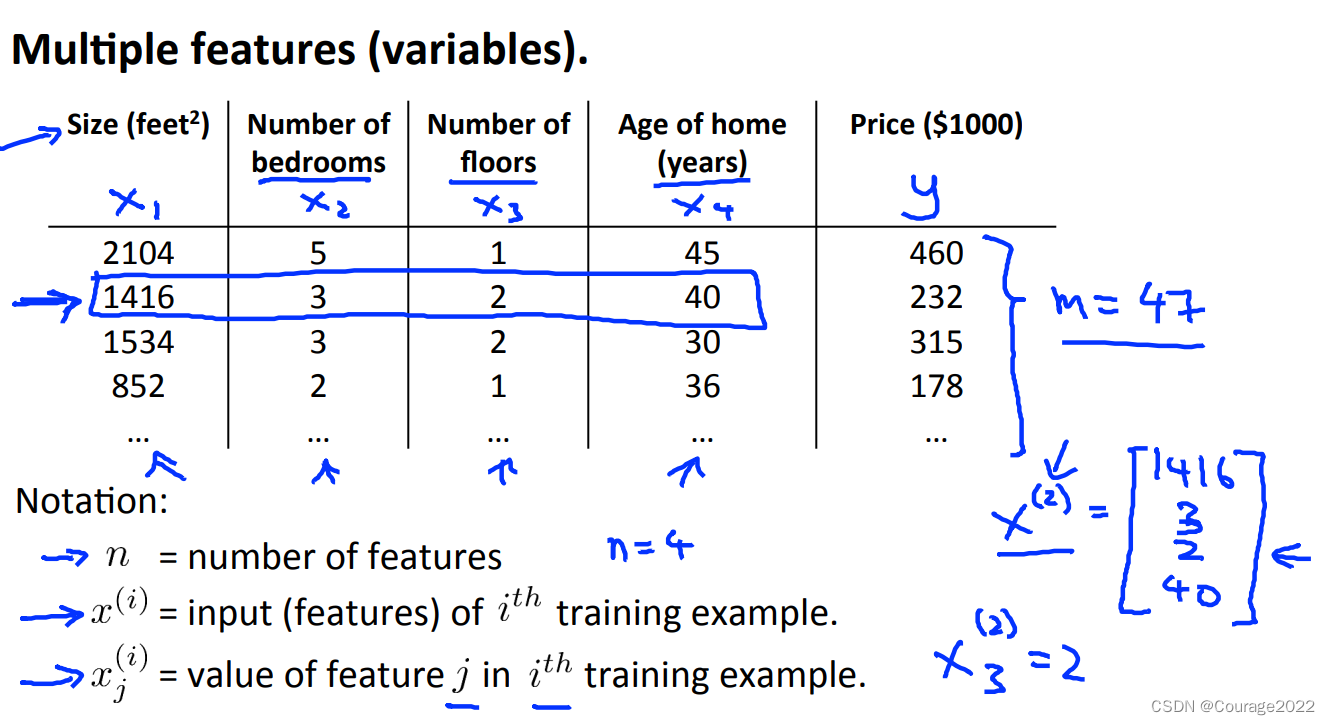
但单一的参数不能够描述一个模型，比如房价只和房子面积有关吗？它的房龄、地段也同样重要！如下图所示。

3.2 假设函数

类比于单一变量线性回归的假设函数，多元线性回归的假设函数如下：

$h_{\theta}(x) = \theta_{0} + \theta_{1} x_{1} +\theta_{2} x_{2}+\theta_{3} x_{3}+...+\theta_{n} x_{n}$

3.3 代价函数

类比于单一变量线性回归的假设函数，多元线性回归的代价函数如下：

$\jmath (\theta_{0},\theta_{1},\theta_{2}\theta_{3},...\theta_{n}) = \frac{1}{2m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})^2$

3.4 梯度下降

3.4.1 多元线性回归梯度下降算法

类比于单一变量线性回归的假设函数，多元线性回归的梯度下降算法如下：

$\theta_{j} := \theta_{j} -\beta \frac{\partial }{\partial \theta_{j} }\jmath (\theta)$

$\theta{j} := \theta{j} - \alpha \frac{1}{m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})x_{j}^{i}$

3.4.2 多元线性回归梯度下降算法的问题

1.特征缩放（Feature Scalng）

大多数情况下，数据集将包含量级、单位和范围差异很大的要素。

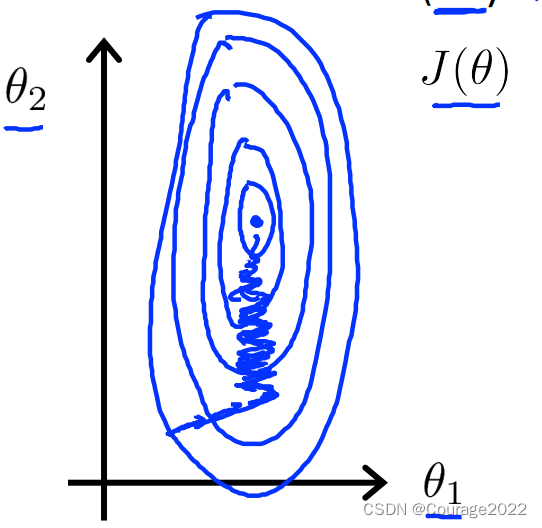
以买房子为例：可能第一个变量为房子面积（0-2000），第二个变量为卧室的数量（1-5），量级差别比较大，我们画出代价函数和参数的关系。

我们在进行梯度下降时，量级大的参数和量级小的参数在进行梯度下降时会有振荡现象发生。导致系统鲁棒性差。

那如何改进呢？

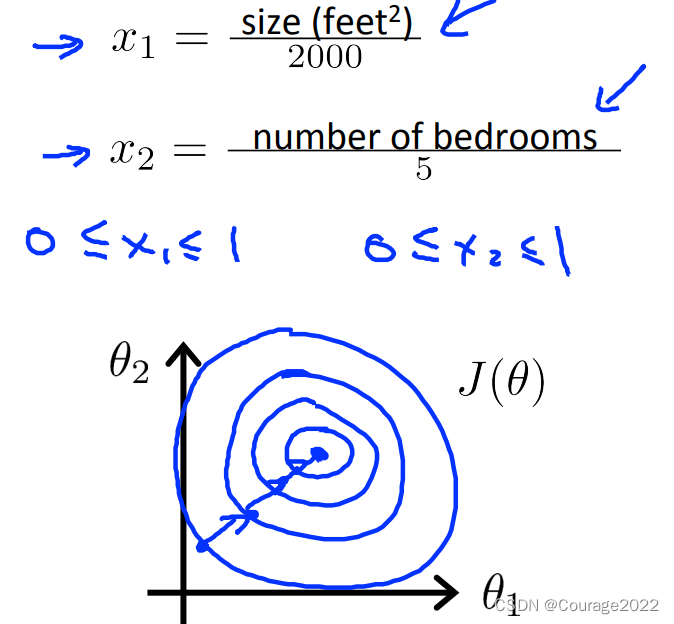
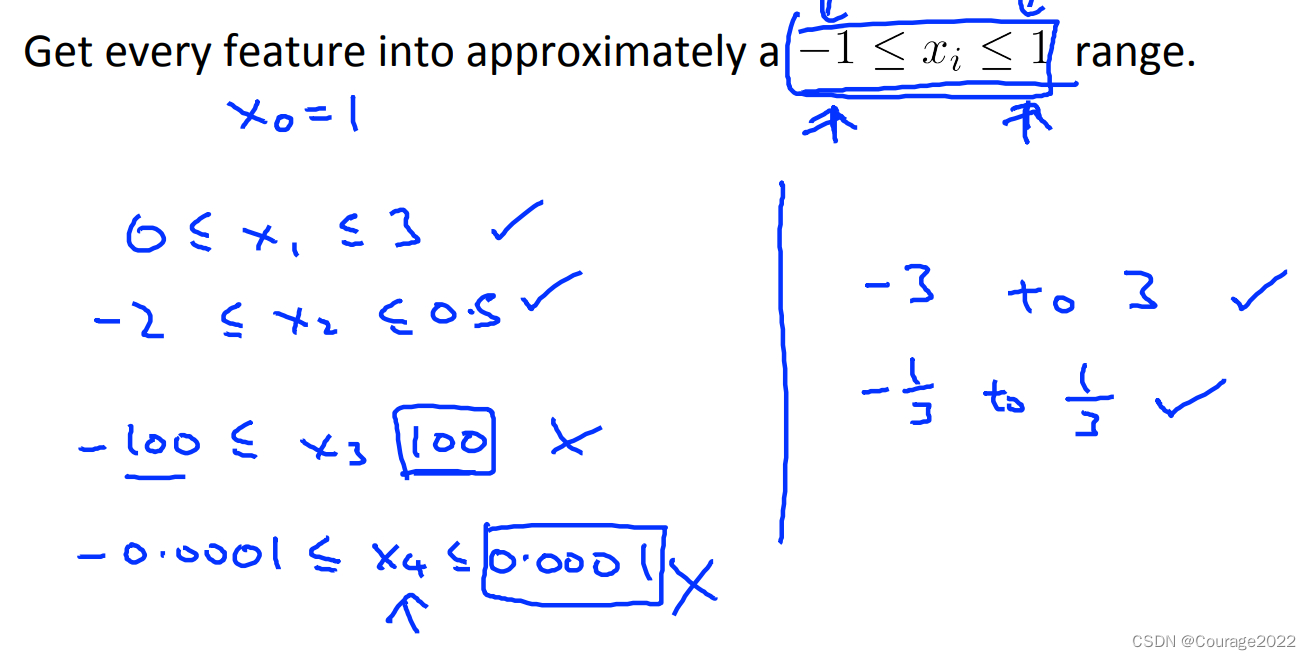
①我们对其进行尺度归一化！如下图所示：

让每个系数都控制在-1~1期间：

②均值归一化

2. 学习率（Learning rate）

对于梯度下降算法 $\theta_{j} =\theta_{j} - \alpha \frac{\partial }{\partial \theta_{j}}\jmath (\theta)$ :

怎么样去确定梯度下降法正确呢？如何去选择学习率呢？怎么确定什么时候梯度下降结束呢？

我们做出最终确定的线性回归方程，做出 $\underset{\theta}{min}\jmath (\theta)$ 与迭代次数的图像

我们设定一个阈值，比如一次下降不超过 $10^{-4}$ 就认为是收敛了。

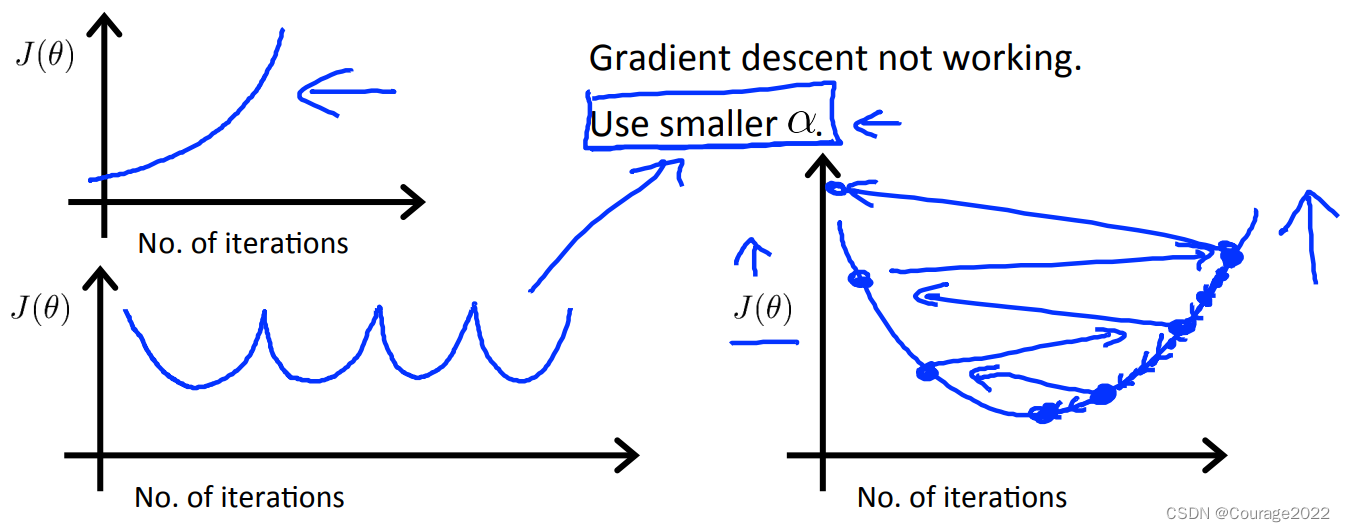
如果随着迭代次数代价越来越高、摇摆不定的话则需要减少学习率。

因此，如果学习率较小，最终会收敛不过收敛的很慢影响效率；若学习率过大，则会难以收敛，我们推荐这么选择学习率。

0.001 -- 0.003 -- 0.01 -- 0.03 -- 0.1 -- 0.3

3.5 多项式回归

3.5.1 问题背景及尺度归一化

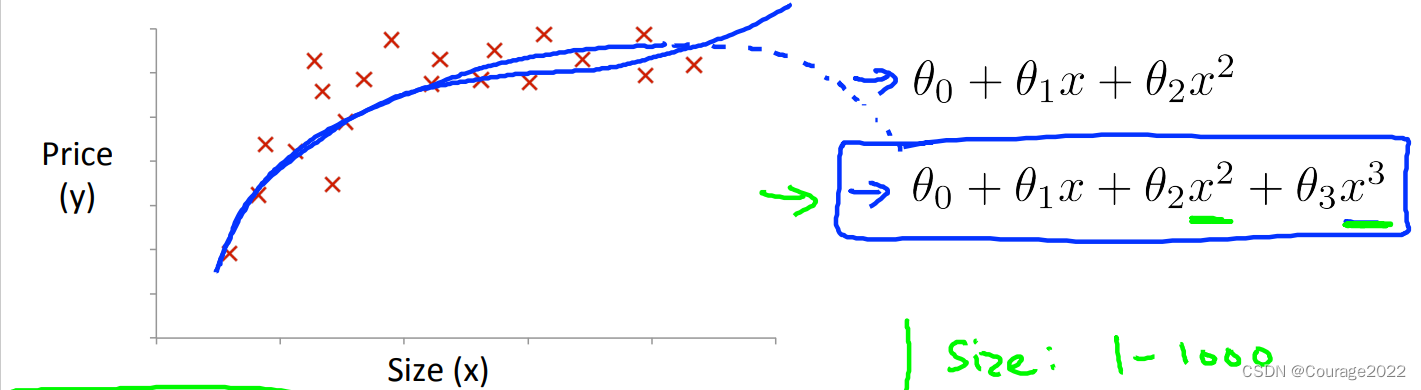
有时候我们用一元函数拟合不好，则我们需要用多项式拟合曲线。

这时，我们的假设方程为

$h_{\theta}(x) = \theta_{0} + \theta_{1}x_{1} + \theta_{2}x_{2} + \theta_{3}x_{3} = \theta_{0} + \theta_{1}\cdot size + \theta_{2}\cdot size^{2} + \theta_{3}\cdot size^{3}$

这里， $x_{1} = size ,x_{2} = size^2 ,x_{3} = size^3$ ，并且我们还要考虑它的尺度一致性，比如size的大小范围为（1-100），我们要对其进行尺度归一化。

3.5.2 正则方程求参数最优解

对于单参数方法，对于学过微积分的我们来说 $\jmath (\theta)$ 求其最小值（ $\jmath (\theta) = a\theta^2 + b\theta + c$ ）其实就是求导让其为零求得的 $\theta$ 。

对于多参数方法， $\theta \in \mathbb{R}^{n+1}$ ， $\jmath (\theta_{0},\theta_{1},\theta_{2}......\theta_{m})$ ，对于每个参数，我们让其偏导数让其为 $0$ 的 $\theta_{j}$ 就是最优解的 $\theta_{j}$ 。

我们也可以用正则方程来求最优的 $\theta$ ：

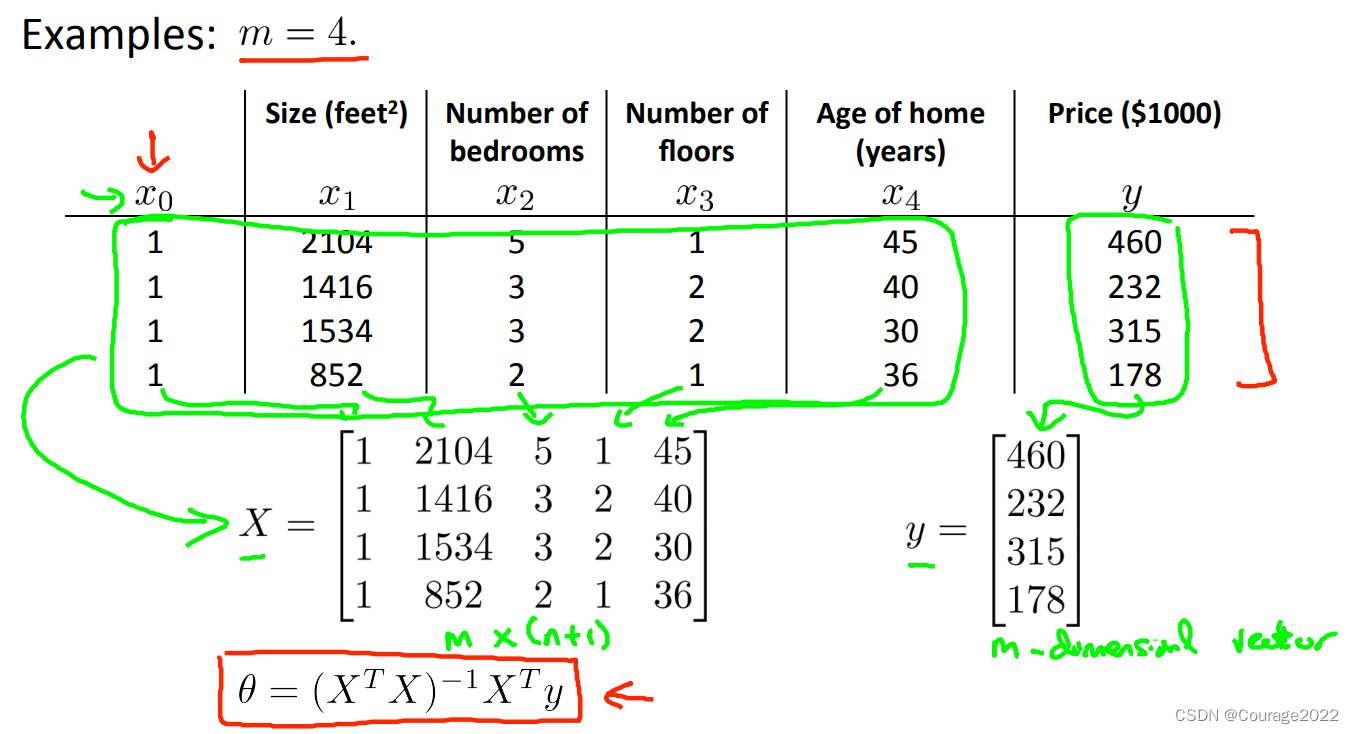
如上图，我们有一个四个数据集的数据，我们构造 $X$ 矩阵， $X$ 矩阵的第一列为1，其他列为不同属性值，我们可用 $\theta = (X^TX)^{-1}X^Ty$ 求的最优 $\theta_{j}$ 的解。

3.5.3 正则方程法 vs 梯度下降法

正则方程化的特点：

①不用去考虑学习率 $\alpha$

②不需要迭代

③需要去计算 $X^TX$ ，这在特征很大（>10000）是个规模庞大的计算，同时 $X$ 也需要一个可逆矩阵（不可逆也可以，虽然这在线性代数里的理解是不行的，但机器会把他优化）

梯度下降法的特点：

①需要去考虑学习率 $\alpha$

②需要迭代

③能在特征数很大的时候也能算