【Simulink】PSO算法优化Simulink模型的参数在线整定（二）一一一高阶不稳定系统

阅读须知：
1.参考文献：张继荣,张天.基于改进粒子群算法的PID控制参数优化[J].计算机工程与设计,2020,41(04):1035-1040.
2.其中仿真模型与算法均按照文中所搭建与设置。

---

1.学习目标：

1.掌握Simulink与m文件的数据交互；
2.传递函数的表达形式，m文件编写与Simulink文件；
3.运用算法进行Simulink仿真优化的在线参数整定。

---

2.学习内容：

1、 两种数据交互的形式----Simulink仿真与m文件

**第一种是：**在这里可以运用assignin命令将参数赋予到基础工作区，并运用sim命令驱动Simulink文件进行在线仿真运行。

function z=PSO_PID(x)

assignin('base','Kp',x(1));  %将值 x(1) 赋予MATLAB 基础工作区中的变量 Kp
assignin('base','Ki',x(2));
assignin('base','Kd',x(3));

[t_time,x_state,y_out]=sim('PID_Model',[0,20]); %% [0,20] 系统仿真的时间范围（起始至终止时间）
% t_time 返回系统仿真的时间向量
% x_state 返回系统仿真的状态变量矩阵
% y_out 返回系统仿真的输出矩阵
z=y_out(end,1);

**第二种是：**通过在Simulink文件中设置 “To Workspace”模块，如下所示，并设置所输出的变量名和类型，可选择矩阵序列或者带时间的数据包等。

设置如下：

运行结果如下：

2、 传递函数的表达形式，m文件编写与Simulink文件

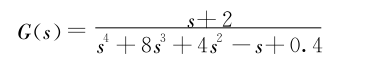
第一种、m文件编写，如下：

sys=tf([1,2],[1,8,4,-1,0.4]);

依据差分方程与Z变换，将上述连续频域下的传递函数继续离散化，可得如下：

clc;
%% 定义传递函数
ts=0.01;
sys=tf([1,2],[1,8,4,-1,0.4]); %%   
dsys=c2d(sys,ts,'z');
[num,den]=tfdata(dsys,'v');

rin=1.0;
u_1=0.0;u_2=0.0;
y_1=0.0;y_2=0.0;
x=[0,0,0]';
error_1=0;
P=1000;

%% 定义PID控制参数
Kpidi(1) = 200;%0-30
Kpidi(2) = 0;%0-1
Kpidi(3) = 100;%0-1

for k=1:1:P
   timef(k)=k*ts;
   r(k)=rin;
   u(k)=Kpidi(1)*x(1)+Kpidi(2)*x(2)+Kpidi(3)*x(3); 
   
   if u(k)>=10
      u(k)=10;
   end
   if u(k)<=-10
      u(k)=-10;
   end   
   
   yout(k)=-den(2)*y_1-den(3)*y_2+num(2)*u_1+num(3)*u_2;
   error(k)=r(k)-yout(k);
   
%------------ Return of PID parameters -------------
   u_2=u_1;u_1=u(k);
   y_2=y_1;y_1=yout(k);
   
   x(1)=error(k);                % Calculating P
   x(2)=(error(k)-error_1)/ts;   % Calculating D
   x(3)=x(3)+error(k)*ts;        % Calculating I
   error_2=error_1;
   error_1=error(k);

end
%% 计算各指标性能
    delt_err = 2e-2;%稳态调整精度，上下允许的偏差
    M=size(yout,1);  %M=1,N=1000
    N=size(yout,2);  %M为运算维度，N为时间序列长度
    N1=(round(N*0.618));
    f_infty=mean(yout(:,N1:N));%稳态值序列,取最终末尾的数据平均值
    err=yout-f_infty*ones(1,N);%通过稳态值计算误差序列,稳态偏差数组
    effect_err = roundn(mean(err(:,N1:N)),-8); %%行列颠倒了很可能就是这个原因
    
    ferr=fliplr(abs(err));     %倒序并取绝对值
    [~,ts_i]=max(ferr>delt_err*f_infty,[],2); %误差绝对值倒序 
% M = max(A,[],dim) 返回维度 dim 上的最大元素。例如，如果 A 为矩阵，则 max(A,[],2) 是包含每一行的最大值的列向量    
    ts_i=N*ones(M,1)-ts_i;
    Ts=ts_i*ts;%调节时间
    [fp,tp]=max(yout,[],2);%峰值和函数峰值
    tp=tp*ts;
    tp(abs(fp-f_infty)<1e-5)=NaN; %过阻尼无超调，没有峰值时间
    sigma=(fp-f_infty)./f_infty;
    
        if  M==1 %非调试模式下不显示
        disp(['系统稳态值为',num2str(f_infty)]) 
        disp(['系统稳态误差为',num2str(effect_err),' r/min'])
        disp(['系统超调量为',num2str(sigma*100),' %'])
            if isnan(tp)
                disp('系统不存在峰值时间')
                else
                disp(['系统峰值时间为',num2str(tp),' s'])
            end
        disp(['系统的调节时间为',num2str(ts),' s'])
        end
%% 转速阶跃上升的绘图
clf;
figure(1);
plot(timef,rin,'r',timef,yout,'b');
yout';
xlabel('Time(s)');ylabel('rin,yout');

运行结果如下：

由上可知，三个参数kp、ki和kd未整定，从而导致系统的阶跃响应输出不是有限稳定的，为此，运用优化算法来进行整定。

第二种：Simulink文件搭建，如下：

3. 运用算法进行Simulink仿真优化的在线参数整定

采取的适应度是ITAE，运用PSO优化算法，读者可自行尝试其他的优化算法。或者私我，诸如遗传算法、简单的优化算法和多目标遗传算法等博主均已实现。

主函数 PSO

%% 清空环境
close all;
clear;
clc;
tic;
%% 参数设置
w = 0.6;      % 惯性因子 ---可设置为变化的
c1 = 2;       % 加速常数
c2 = 2;       % 加速常数

Dim = 3;            % 维数
SwarmSize = 5;    % 粒子群规模
ObjFun = @PSO_PID;  % 待优化函数句柄

MaxIter = 10;      % 最大迭代次数  
MinFit = 0.1;       % 最小适应值 

Vmax = 1;
Vmin = -1;

Lb = [0 0 0];
Ub = [300 300 300];


%% 粒子群初始化
    Range = ones(SwarmSize,1)*(Ub-Lb);
    Swarm = rand(SwarmSize,Dim).*Range + ones(SwarmSize,1)*Lb;      % 初始化粒子群
    VStep = rand(SwarmSize,Dim)*(Vmax-Vmin) + Vmin;                 % 初始化速度
    fSwarm = zeros(SwarmSize,1);
for i=1:SwarmSize
    fSwarm(i,:) = feval(ObjFun,Swarm(i,:));                         % 粒子群的适应值
end

%% 个体极值和群体极值
[bestf bestindex]=min(fSwarm);
zbest=Swarm(bestindex,:);   % 全局最佳
gbest=Swarm;                % 个体最佳
fgbest=fSwarm;              % 个体最佳适应值
fzbest=bestf;               % 全局最佳适应值

%% 迭代寻优
iter = 0;
y_fitness = zeros(1,MaxIter);   % 预先产生4个空矩阵
K_p = zeros(1,MaxIter); %% MaxIter 最大迭代次数        
K_i = zeros(1,MaxIter);
K_d = zeros(1,MaxIter);

while( (iter < MaxIter) && (fzbest > MinFit) )
    for j=1:SwarmSize
        % 速度更新
        VStep(j,:) = w*VStep(j,:) + c1*rand*(gbest(j,:) - Swarm(j,:)) + c2*rand*(zbest - Swarm(j,:));
        if VStep(j,:)>Vmax, VStep(j,:)=Vmax; end
        if VStep(j,:)<Vmin, VStep(j,:)=Vmin; end
        % 位置更新
        Swarm(j,:)=Swarm(j,:)+VStep(j,:);
        for k=1:Dim
            if Swarm(j,k)>Ub(k), Swarm(j,k)=Ub(k); end
            if Swarm(j,k)<Lb(k), Swarm(j,k)=Lb(k); end
        end
        % 适应值
        fSwarm(j,:) = feval(ObjFun,Swarm(j,:));
        % 个体最优更新     
        if fSwarm(j) < fgbest(j)
            gbest(j,:) = Swarm(j,:);
            fgbest(j) = fSwarm(j);
        end
        % 群体最优更新
        if fSwarm(j) < fzbest
            zbest = Swarm(j,:);
            fzbest = fSwarm(j);
        end
    end 
    iter = iter+1;                      % 迭代次数更新
    y_fitness(1,iter) = fzbest;         % 为绘图做准备
    K_p(1,iter) = zbest(1);
    K_i(1,iter) = zbest(2);
    K_d(1,iter) = zbest(3);
end
%% 绘图输出
clf;
figure(1)      % 绘制性能指标ITAE的变化曲线
plot(y_fitness,'LineWidth',2)
title('最优个体适应值','fontsize',18);
xlabel('迭代次数','fontsize',18);
ylabel('适应值','fontsize',18);
set(gca,'Fontsize',18);

figure(2)      % 绘制PID控制器参数变化曲线
plot(K_p,'k','LineWidth',3);
hold on
plot(K_i,'r','LineWidth',3);
hold on
plot(K_d,'--b','LineWidth',3);
title('Kp、Ki、Kd 优化曲线','fontsize',18);
xlabel('迭代次数','Fontsize',18);
ylabel('参数值','Fontsize',18);
set(gca,'Fontsize',18);
legend('Kp','Ki','Kd');
toc;

驱动Simulink模型的子函数，PSOPID

function z=PSO_PID(x)

assignin('base','Kp',x(1));  %将值 x(1) 赋予MATLAB 基础工作区中的变量 Kp
assignin('base','Ki',x(2));
assignin('base','Kd',x(3));

[t_time,x_state,y_out]=sim('PID_Model',[0,20]); %% [0,20] 系统仿真的时间范围（起始至终止时间）
% t_time 返回系统仿真的时间向量
% x_state 返回系统仿真的状态变量矩阵
% y_out 返回系统仿真的输出矩阵
z=y_out(end,1);
...

运行结果如下：

---

3.学习产出：

提示：这里统计学习计划的总量
1、 笔记 1 遍
2、CSDN 技术博客 1 篇
3、可运行的代码，基于博主的代码可自行搭建并改进PSO。

---