正项级数及其审敛法

最新推荐文章于 2024-06-05 20:29:17 发布
最新推荐文章于 2024-06-05 20:29:17 发布
阅读量8.6k 收藏 20
点赞数 5
分类专栏： 无穷级数 高数
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_42578970/article/details/106767123
版权

一般的常数项级数，各项可以为正数负数或零，我们把只有正数和零的级数称为正项级数。

定理1：正项级数收敛的充要条件是他的部分和数列{sn}有界

sn=u1+u2+...+un

定理2：若un之和与vn之和都是正项级数，对于任意n，un<=vn，若vn之和收敛，则un之和也收敛，反之，若un之和发散，则vn之和也发散

定理3：若un之和与vn之和都是正项级数，若

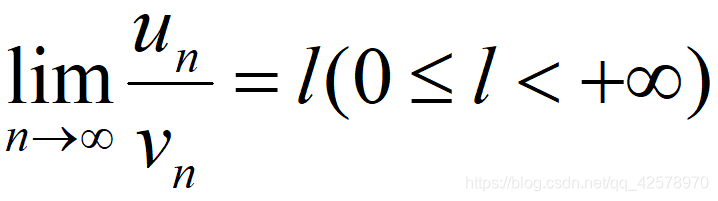
且vn之和收敛，则un之和收敛

若

且vn之和发散，则un之和发散

定理4：设un之和为正项级数，若

p大于1，包括为正无穷时，发散，小于1，收敛，等于1，两种情况都有可能

定理5：如果un之和为正项级数，若

当p小于1，收敛，大于1，发散，等于1，两种情况都有可能

定理6：若

则发散，若

则收敛

此外，可以使用等价无穷小或泰勒展开来化简或改变式子，然后再采用上面的某种方法。展开或替换后的式子与原式同散敛性

数项级数——（二）正项级数
qq_45011547的博客
05-16 8180
一.正项级数收敛性的一般判别 同号级数；正项级数； 由于级数与其部分和数列具有相同的敛散性，得如下定理。 定理1. 正项级数收敛的充要条件是：部分和数列有界，即存在某正数M，对一切正整数n有 定理2.（比较原则） 设和是两个正项级数，如果存在某正数N，对一切n>N都有则 （i）若级数收敛，则级数也收敛； （ii）若级数发散，则级数也发散； （大收小发） 推论 设 ...
两种正项级数比较审敛法极限形式的不同表述
Bing's Blog
11-03 1万+
正项级数的比较审敛法是较好用的方法。尤其是它的极限形式更为常用。 在一般高数书本上，表述如下： 设limn→+∞unvn=l,l∈[0,+∞]\lim_{n\rightarrow +\infty}{u_n\over v_n} = l, l\in [0,+\infty] 则： 若0<l<+∞0 < l < +\infty,∑∞n=1un与∑∞n=1vn\sum_{n=1}^\infty u_n与
【高等数学】下册 第十二章 第二节 常数项级数的审敛法
weixin_45725295的博客
09-11 2268
1. 正项级数及其审敛法 1.1. 正项级数 1.1.1. 定义 1.1.2. 比较审敛法 1.2. p级数 1.2.1. 定义 1.2.2. 收敛性 1.3. 比较审敛法的极限形式 1.3.1. 定理 1.3.2. 比值审敛法 1.3.3. 根值审敛法 1.3.4. 极限审敛法 2. 交错级数及其审敛法 2.1. 交错级数的定义 2.2. 莱布尼茨定理 3. 绝对收敛与条件收敛 3.1. 定义 3.2. 定理
【高数】正项级数及其审敛法
qq_42482533的博客
05-26 275
并不是满足第一门槛就是收敛级数 详 定理2重要 大于一的情况不看 下面根据P的范围判断级数->重点 证明发散，就要让它大于某一个级数为发散的式子
第三讲 正项级数的比较审敛法
热门推荐
小访客的博客
11-28 3万+
一，用比较审敛法的原因 对于大多数级数，很难得到部分和的表达式，因此很难用定义来研究其敛散性 比较审敛法不能用于非正项级数 二，正项级数 定义：，其中 部分和为单调递增数列 收敛的充要条件：有上界 推论：若无界，则发散，且 正项级数结合律：发散+发散=发散 三，正项级数的比较审敛法 设和是正项级数，且，（） 若收敛，则收敛 若发散，则发散 四，p-级数的敛散性 定义：，（） ...
高数笔记（二十）：无穷级数，级数的审敛法
xuuyann
05-03 2382
写在前面 当初考研时的手写笔记，不喜勿看，作为个人笔记电子档留存。
级数_2：常数项级数的审敛法
weixin_45504690的博客
04-28 2754
文章目录正项级数 正项级数 定义：若un≥0，则称∑n=1∞un为正项级数。定义：若u_n\ge0，则称\sum_{n=1}^{\infty}u_n为正项级数。定义：若un​≥0，则称∑n=1∞​un​为正项级数。 定理1：定理1：定理1：正项级数收敛⇒部分和序列有界（基础，不常用）正项级数收敛\Rightarrow部分和序列有界（基础，不常用）正项级数收敛⇒部分和序列有界（基础，不常用） 定理2...
人大微积分正项级数及其审敛法PPT教案.pptx
10-01
《人大微积分正项级数及其审敛法》是一份深入探讨正项级数收敛性的教学资料，主要涉及微积分中的级数理论。在微积分中，正项级数是研究的重要部分，因为它与实际问题紧密相关，如物理、工程等领域中的无限序列求和。...
人大微积分课件11-2正项级数及其审敛法.ppt
12-07
以下是一些关于正项级数及其审敛法的关键知识点： 1. **正项级数的概念**：如果级数中的每一项都是非负实数，那么这个级数被称为正项级数。记作：∑(n=1 to ∞) nu_n，其中nu_n >= 0。 2. **部分和数列**：正项...
人大微积分课件112正项级数及其审敛法.ppt
02-22
人大微积分课件112正项级数及其审敛法.ppt
人大微积分课件11-3任意项级数及其审敛法.ppt
12-07
《任意项级数及其审敛法》是微积分学习中的一个重要章节，主要涉及交错级数、绝对收敛与条件收敛的概念及判别方法。下面将详细阐述这部分内容。 交错级数是指正负项相间的级数，例如交错级数1 - 1/2 + 1/3 - 1/4 + ...
无穷级数（二）常数项级数的审敛法
AryCra_07的博客
03-03 1974
无穷级数（二）常数项级数的审敛法
2021-03-09
yjy2471598769的博客
03-09 3020
第十四讲 无穷级数 一、级数敛散性的判别方法： 1.正向级数及其判别方法： （1）收敛原则：正向级数 收敛的充分必要条件是它的部分和数列{Sn}有界。 （2）比较判别法：有两个正向级数 若从某项起有Un<=Vn成立，有“大收敛推出小收敛，小发散推出大发散”。 （3）比较判别法的极限形式： 当n趋向于无穷大，Un/Vn = A, 如果A = 0，则Vn收敛时，Un也收敛； 如果A = +无穷，则Vn发散时，Un也发散； 如果0<A<+无穷，二者具有相同的敛散性。 （4）比值判别法： 当n
正项级数的审敛法和交错级数的审敛法
最新发布
fenglijia0627的博客
06-05 1433
1:p<1首先都能找到一个比p稍大或者稍小的数,但不改变与1的关系,设为r吧,接下来把开方或 者分母乘到右边去,然后右边就会形成一个等比数列,因为等比数列(公比小于1)是收敛的,证明:取Vn=1/2*(Un+|Un|),Vn级数肯定是比|Un|级数小的,所以收敛,则2Vn收敛.那么2Vn-|Un|收敛(两收敛级数相加减),则Un收敛.limn->∞时,n次根号下的项如果小于1,则收敛,反之则发散。
比较审敛法
qq_43806430的博客
07-27 2034
高等数学笔记
i78i845的博客
11-21 2282
定理4：如果y1*(x),y2*(x)分别是方程y''+p(x)y'+q(x)y=f1(x) ，y''+p(x)y'+q(x)y=f2(x) 的特解，则y1*(x)+y2*(x)是方程y''+p(x)y'+q(x)y=f1(x)+f2(x)的一个特解。正确解：（1）lim[x->0] (f(x)-x)/x^2=lim[x->0] (f'(x)-1)/2x =1/2 *lim[x->0] (f'(x)-f'(0))/x =f''(0)/2=1。
无穷级数（1）
qq_53711878的博客
08-19 1万+
进入无穷级数章节，在这一章，我们暂时告别了线面积分，转而研究一串式子的和的问题。 一、初识无穷级数 何为无穷级数 给出一个无穷序列, 我们把它们的和式称为无穷级数，简记为，其中是通项。 根据每一项的特征，级数又分为了数项级数和函数项级数。 无穷级数的敛散性 这便是级数敛散性的定义，也是我们判断级数敛散性的第一个手段——求出部分和（前n项和），判断这个部分和是否有极限。 例 虽然计算部分和的极限来判断级数是否收敛这种方法很直接、易懂，但是很多情况下我们很难求.........
数项级数收敛判别
HGGshiwo的博客
03-30 2855
书上没有考虑数列的收敛，可能是太简单了。。。 数项级数判别法知识点较多，总结如下 柯西收敛准则 必要条件无穷远处是 考虑发散可能会用到这个 正项级数 1.部分和数列有界，抽象数列较为常见 2.第一比较判别法，un<vnu_{n}<v_{n}un​<vn​ 3.第二比较判别法，unnpu_{n}n^pun​np或者qnunq^nu_{n}qnun​，nnn无穷大时候的情况(与p幂法...
常数项级数、函数项级数、幂级数与傅里叶级数
weixin_62985761的博客
06-13 1万+
提示：本文的适用对象为已修过《微积分A1》的非数学系学生，文中题型方法为个人总结，为个人复习使用。部分理解虽然不太严谨，但对于解题的实用性较强。若有疏漏or错误，欢迎批评指正。
正项级数敛散判别法实际应用
03-23
正项级数敛散判别法可以用来判断一个正项级数是否收敛。具体来说，如果一个正项级数的通项公式为an，那么当极限lim(n->∞)an=0时，该级数收敛；当极限lim(n->∞)an≠0时，该级数发散。这种方法在数学、物理、工程等...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值