二分法(Bisection Method)原理及改进

最新推荐文章于 2024-04-24 22:52:03 发布

图灵猫

最新推荐文章于 2024-04-24 22:52:03 发布

阅读量1.6k

点赞数 2

文章标签： python 二分法

本文链接：https://blog.csdn.net/qq_42818403/article/details/120558242

版权

非线性方程的二分法(Bisection Method)

文章目录

非线性方程的二分法(Bisection Method)

考虑非线性方程

f (x) = 0

条件

$f(x)\in C[a,b]$ , 且 $f (a) \cdot f (b) < 0$

主要依据

由连续函数介值定理,则至少存在某个 $x^* \in (a,b)$ ,使得 $f(x^*)=0$ ,即 $[a, b]$ 内至少有上述方程的一个根,称 $[a, b]$ 为 $f (x)$ 的一个含根区间.并且有
$|x^*-\frac{a+b}{2}|\le\frac{b-a}{2}$

二分法_1

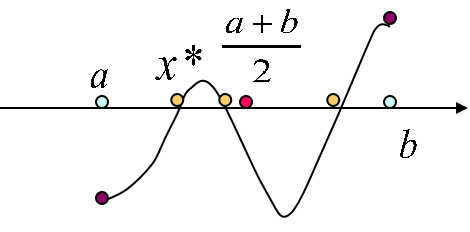
主要思想(基本思想)

把含根区间不断缩短,使含根区间之间含有一个满足误差要求的近似解。

具体过程(方法)

首先,令 $a_1=a,b_1=b,h=b-a$ ,

找中点: $x_1=\frac{1}{2}(a_1+b_1)$ ;
计算: $f_1=f(x_1)$ (即中点的函数值);
生成含根区间:

若 $f(x_1)=0$ ,则 $x^*=x_1$ ,

若 $f(x_1)·f(a_1)>0$ ,则 $a_2=x_1,b_2=b_1$ ,

若 $f(x_1)·f(a_1)<0$ ,则 $a_2=a_1,b_2=x_1$ ,
生成含根区间 $a_2,b_2].[a_2,b_2]$ 满足下式:
$\left\{ \begin{aligned} (1)&\ [a_2,b_2 ]\in [a_1,b_1]\\ (2)&\ b_2-a_2= \frac{h}{2} \\ (3)&\ f(a_2)·f(b_2)\le 0 \end{aligned} \right.$
以 $a_2,b_2]$ 取代 $a_1,b_1]$ ,继续以上过程,得到 $[a_3,b_3]\dots$

优缺点

优点

对函数要求低(只要连续,在两个端点异号).
二分法是收敛的.

缺点

收敛速度不快,仅与公比为 $\frac{1}{2}$ 的等比级数的收敛速度相同.即是线性收敛的.
不能用于求偶重根、复根；不能推广到多元方程组求解.

例如:

$x^2=0,x\in [-1,1]$
$x^2+1=0$
不能求出所有根,(即有可能漏根).

如下图,当方程 $f (x) = 0$ 存在多个根时,传统二分法最多只能找到1个根,而漏掉其余多个根.

二分法_2

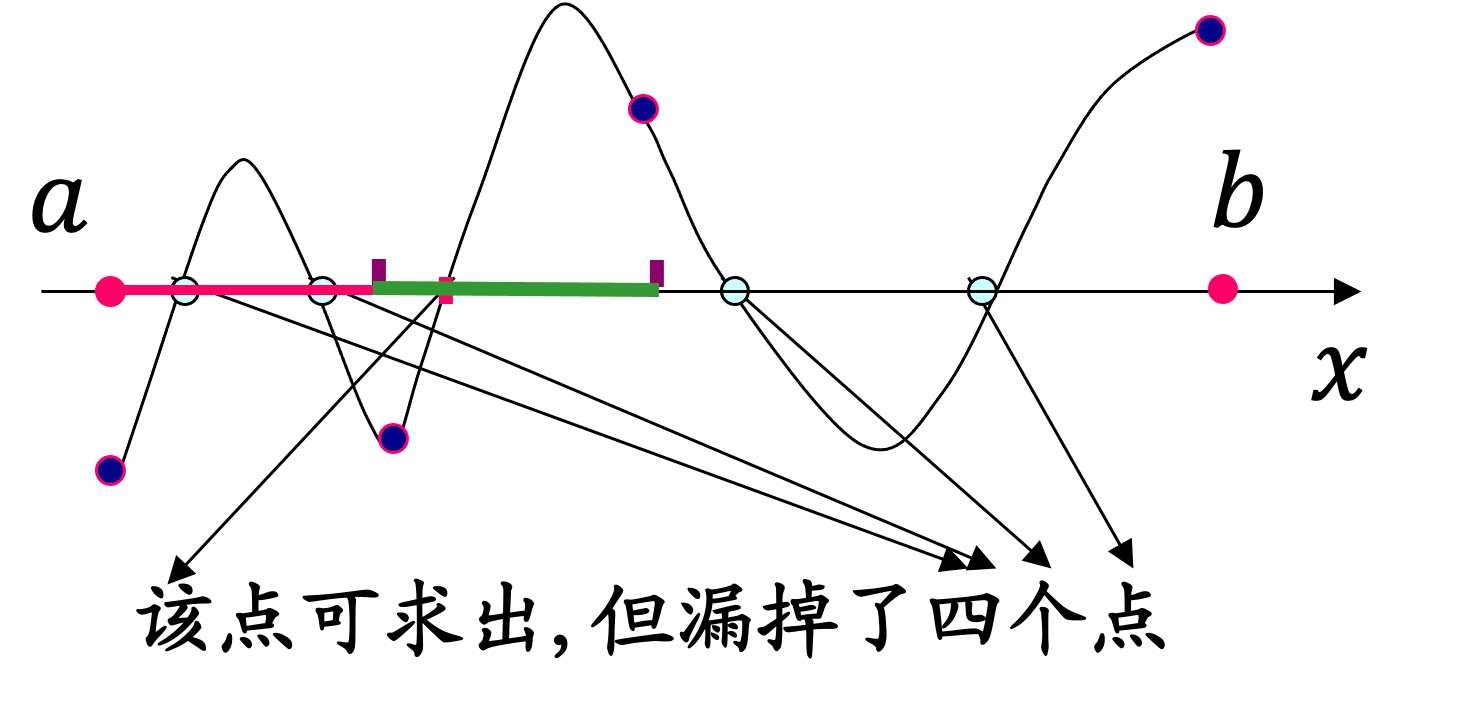
改进方法

针对缺点3,对在区间 $[a, b]$ 上存在 $m$ 个实根的方程 $f (x) = 0$ ,拟提出如下两种改进算法:

改进方法 1

Step1: 通过二分法得到第一个近似根 $x_1$ ;
Step2: 取 $x_1$ 的最后一次搜索区间 $x_1^-,x_1^+]$ ,考虑其端点函数值 $f(x_1^-)$ 与 $f(x_1^+)$ 的符号;
Step3: 选取 $f(x_1^-),f(x_1^+)$ 与异号的区间端点函数值 $f (a), f (b)$ 配对进行二分求根算法,分别得到两个近似根 $x_2,x_3$ ;
Step3: 继续执行 Step2-Step3,直到找到 $m$ 个满足条件的根.

经检验,此算法不保证能够找出所有满足条件的根.(例如:两根之间的距离充分小)

改进方法 2

Step1: 对求解区间 $[a, b]$ 做网格剖分,取正整数 $n$ .将 $[a, b]$ 作 $n$ 等分.记 $h=\frac{b-a}{n};x_i=ih,0\le i\le n$ .
Step2: 从第一个子区间 $x_i,x_{i+1}],i=0$ ,开始判定
- 是否满足: $f(x_i)=0\ 或者\ f(x_{i+1})=0$
  - 是:得到 $x_i\ 或\ x_{i+1}$ 作为近似根 $x_{i+\frac{1}{2}}$ ;
  - 否:执行后续判定.
- 是否满足: $f(x_i)·f(x_{i+1})<0$
  - 是:在区间 $x_i,x_{i+1}]$ 上通过二分法得到近似根 $x_{i+\frac{1}{2}}$ ;
  - 否:继续向后判定是否满足: $f(x_i)·f(x_{i+2})<0$ ,直到完成对整个区间 $[a, b]$ 的判定,退出循环.
Step3: 选择近似根 $x_{i+\frac{1}{2}}$ 的邻近点 $x_{i+\frac{1}{2}}^+$ 或者 $x_{i+\frac{1}{2}}^-$ 与 $x_{i+2}$ 配对执行二分法.
Step4: 继续执行 Step2-Step3,判断是否能够找到 $m$ 个满足条件的根.
- 是:输出结果;
- 否:加密网格( $h=\frac{h}{2}$ ).
Step5: 继续执行 Step2-Step3,直到找到 $m$ 个满足条件的根.

Python 代码部分

利用二分法(Bisection Method)求解在区间 $[a, b]$ 上存在 $m$ 个实根的方程 $f (x) = 0$ 的Python代码如下:

m_roots.py:

# 开发者:    Leo 刘
# 开发环境: macOs Big Sur
# 开发时间: 2021/9/24 11:55 下午
# 邮箱  : 517093978@qq.com
# @Software: PyCharm
# ----------------------------------------------------------------------------------------------------------
"""
    主函数功能：
    寻找f(x) = sin(x)在指定区间[a,b]上的所有根
    输出区间端点函数值
    绘制函数图像
"""
import numpy as np
import matplotlib.pyplot as plt


def fun(x):
    # 方程等号左边函数f(x)

    return np.sin(x)


def sign(val):
    # 符号函数

    if val < 0:
        s = "-"

    elif val > 0:
        s = "+"

    else:
        s = "0"

    return s


def main(a, b, step=0.01):
    i = 0
    roots = []
    roots_interval = []
    root_counter = 0
    signs = ""
    # 打印f(x)的符号
    print("-" * 38)
    # print("近似解x\t\t\t函数值\t\t函数值符号")
    for x in np.arange(a, b, step):
        # print("-" * 38)
        val = fun(x)
        signs = signs + sign(val)
        # print("%.6f \t\t%.6f\t\t %s" % (x, val, sign(val)))
        if i > 0 and (signs[i - 1] == 0 or signs[i - 1] != signs[i]):
            root_counter += 1
            if signs[i - 1] == '0':
                roots = np.append(roots, x - step)
            if signs[i - 1] != signs[i] and signs[i - 1] != '0':
                roots_interval = np.append(roots_interval, x)
        i += 1

    # print("-" * 38)
    print("方程在区间[%.4f,%.4f]上根的个数为：%d" % (a, b, root_counter))
    print("准确解%d个，分别为:" % len(roots), roots)
    print("近似解%d个，所在区间分别为:" % len(roots_interval))
    for k in range(len(roots_interval)):
        print("[%.6f,%.6f]  " % (roots_interval[k] - step, roots_interval[k]), end='')

    # #  绘图
    # plt.figure(figsize=(8, 4))
    # plt.plot(np.arange(a, b, step), np.zeros_like(np.arange(a, b, step)), "k")
    # plt.plot(np.arange(a, b, step), fun(np.arange(a, b, step)), "b", label="$sin(x)$")
    #
    # plt.xlabel("$x$")
    # plt.ylabel("$f(x)$")
    # plt.title("Example")
    #
    # plt.ylim(-1.5, 1.5)
    # plt.legend()  # 显示左下角的图例
    #
    # plt.show()
    return root_counter


if __name__ == '__main__':
    main(0, 10)

m_roots.py程序运行结果:

--------------------------------------
方程在区间[0.0000,10.0000]上根的个数为：4
准确解1个，分别为: [0.]
近似解3个，所在区间分别为:
[3.140000,3.150000]  [6.280000,6.290000]  [9.420000,9.430000]

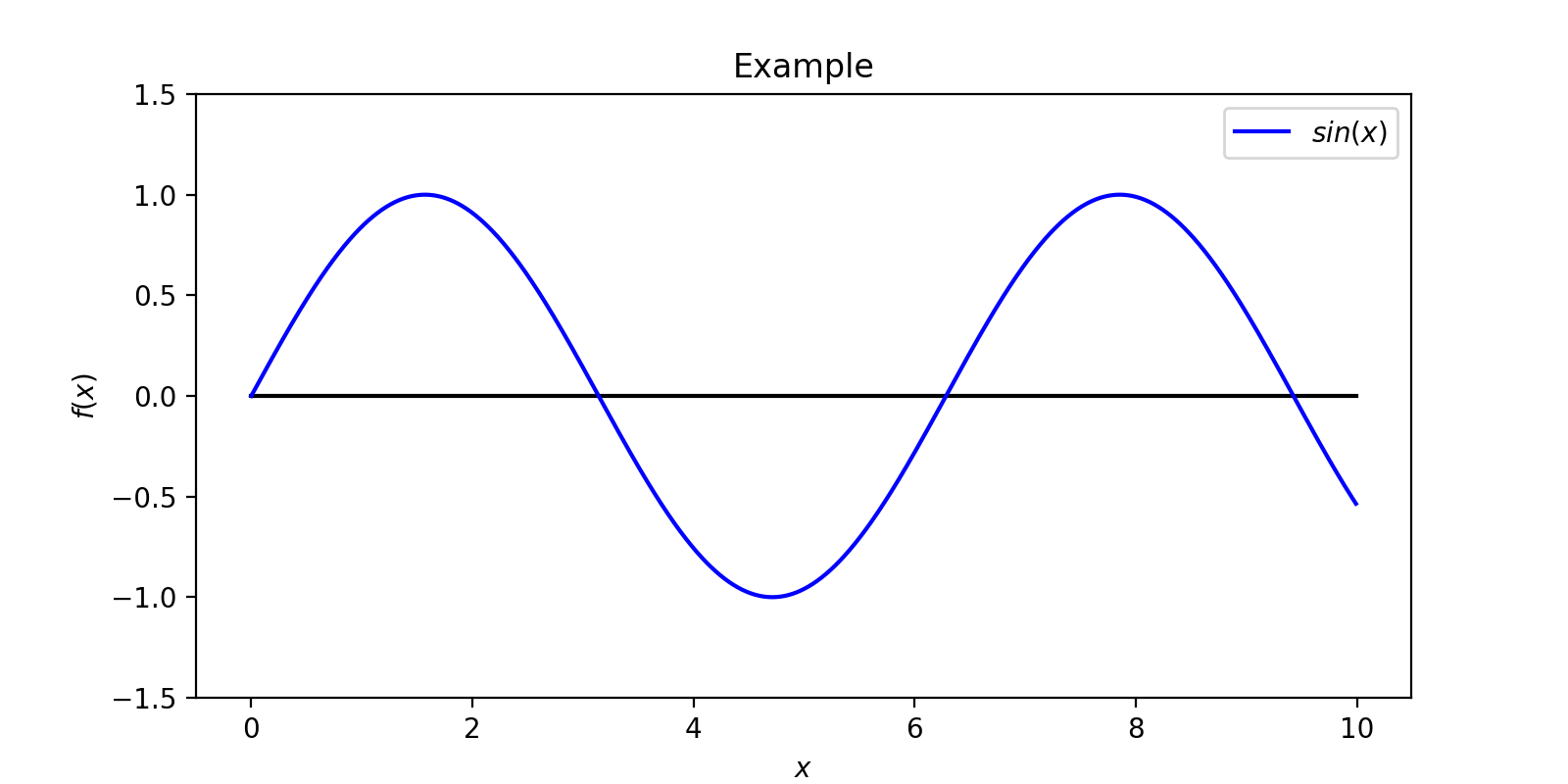
m_roots.py程序运行结果(图示):

二分法程序运行结果

Bisection2roots_promax.py:

# 开发者:    Leo 刘
# 开发环境: macOs Big Sur
# 开发时间: 2021/9/24 5:05 下午
# 邮箱  : 517093978@qq.com
# @Software: PyCharm
# ----------------------------------------------------------------------------------------------------------

"""
    主函数功能：
    使用二分法求方程f(x) = sin(x) = 0在区间[-1,15]内的实根
    近似解的误差限EPS: 1e-6
    函数值误差限ETA: 1e-8

"""
import sys

import numpy as np


# 定义二分法类
class bisectionSolver:
    def __init__(self, a0, b0, EPS, ETA):
        """

        :param a0: 根的存在区间左端点
        :param b0: 根的存在区间右端点
        :param EPS: 近似解的误差限
        :param ETA: 函数值误差限
        """
        self.a0 = a0
        self.b0 = b0
        self.EPS = EPS
        self.ETA = ETA
        self.root_counter = 0  # 根计数器

    # 待求解非线性方程
    @staticmethod
    def fun(x):
        return np.sin(x)

    # 符号函数
    @staticmethod
    def sign(val):
        if val < 0:
            s = "-"
        elif val > 0:
            s = "+"
        else:
            s = "0"
        return s

    # 二分法求解器方法
    def bisectionSolver(self, a0, b0, EPS, ETA):
        a = np.array([a0])

        b = np.array([b0])

        # x = np.array([self.midVal(a, b)])
        x = np.array([np.mean(np.array([a, b]))])
        # 判断x0是否是解
        if np.abs(self.fun(x[0])) < ETA:
            print("    经判断，第%d步达到停止准则: |f[%.6f]| = %.6f < ETA"
                  % (1, self.fun(x[0]), ETA))
            self.root_counter += 1
            return x[0], 0
        print("二分法求解非线性方程数值结果".center(56))
        # print('-' * 66)
        # print("步数\t\t\t", "近似解\t\t\t\t\t", "解区间\t\t\t\t", "函数值")
        N = 100  # 最大迭代步
        for k in range(0, N, 1):
            # print('-' * 66)
            # print("第%d步\t\t" % (k + 1), "%.6f\t\t" % x[k], "[%.6f, %.6f]\t\t" % (a[k], b[k]), "%.6f" % self.fun(x[k]))

            fL = self.fun(a[k])

            fR = self.fun(b[k])

            fx = self.fun(x[k])

            # 决定有根子区间

            if fL * fx < 0:

                a = np.append(a, a[k])

                b = np.append(b, x[k])

                x = np.append(x, np.mean(np.array([a[k + 1], b[k + 1]])))

            elif fx * fR < 0:

                a = np.append(a, x[k])

                b = np.append(b, b[k])

                x = np.append(x, np.mean(np.array([a[k + 1], b[k + 1]])))

            if np.abs(self.fun(x[k + 1])) < ETA:
                print('-' * 66)
                print("第%d步\t\t" % (k + 2), "%.6f\t\t" % x[k + 1], "[%.6f, %.6f]\t\t" % (a[k + 1], b[k + 1]),
                      "%.6f" % self.fun(x[k + 1]))
                print('-' * 66, '\n')
                print("    经判断，第%d步达到停止准则: |f[%.6f]| = %.6f < ETA"
                      % (k + 2, x[k + 1], np.abs(self.fun(x[k + 1]))))
                self.root_counter += 1
                return x[k + 1], k + 2, a[k], b[k]

            if np.abs(self.fun(a[k + 1])) < ETA:
                print("    经判断，第%d步达到停止准则: |f[a[%d]]| = %.6f < ETA"
                      % (k + 1, k + 1, np.abs(self.fun(a[k + 1]))))
                self.root_counter += 1
                return a[k + 1], k + 1, a[k], b[k]

            if np.abs(self.fun(b[k + 1])) < ETA:
                print("    经判断，第%d步达到停止准则: |f[b[%d]]| = %.6f < ETA"
                      % (k + 1, k + 1, np.abs(self.fun(b[k + 1]))))
                self.root_counter += 1
                return b[k + 1], k + 1, a[k], b[k]

            if np.abs(a[k + 1] - b[k + 1]) < EPS:
                print('-' * 66)
                print("第%d步\t\t" % (k + 1), "%.6f\t\t" % x[k + 1], "[%.6f, %.6f]\t\t" % (a[k + 1], b[k + 1]),
                      "%.6f" % self.fun(x[k + 1]))
                print('-' * 66, '\n')
                print("    经判断，第%d步达到停止准则: b[%d] - a[%d] = %.6f < EPS"
                      % (k + 1, k + 1, k + 1, b[k + 1] - a[k + 1]))
                self.root_counter += 1
                return x[k + 1], k + 1, a[k], b[k]


# 主函数

def main(a, b, EPS, ETA):
    """

    :param a: 区间左断点
    :param b: 区间右断点
    :param EPS: 近似解的误差限
    :param ETA: 函数值误差限
    """
    bisecSolver = bisectionSolver(a, b, EPS, ETA)
    fa = bisecSolver.fun(a)
    fb = bisecSolver.fun(b)
    if fa * fb > 0:
        print("端点函数值计算结果：")
        print("f(a)=%.6f" % fa)
        print("f(b)=%.6f" % fb)
        print("f(a)*f(b)=%.6f" % (fa * fb))
        print("抱歉亲！端点函数值同号，不满足二分法启动条件，请重新输入合适的区间后运行！")
        sys.exit(1)

    if np.abs(fa) < ETA:
        print("经判断，第%d步达到停止准则: |f(a[%d])| = %.6f < ETA".center(50)
              % (0, 0, fa))
        print(f"综上，区间左端点a即为近似解: {a:.6f}，此时函数值为: {bisecSolver.fun(a):.6f}")
        bisecSolver.root_counter += 1

    elif np.abs(fb) < ETA:
        print("经判断，第%d步达到停止准则: |f(b[%d])| = %.6f < ETA".center(50)
              % (0, 0, fb))
        print(f"综上，区间右端点b即为近似解: {b:.6f}，此时函数值为: {bisecSolver.fun(b):.6f}")
        bisecSolver.root_counter += 1
    else:

        # 手动判断一阶导数大于零，因此有唯一解
        (x, n, a_k, b_k) = bisecSolver.bisectionSolver(a, b, EPS, ETA)
        print(f"综上，经过{n:d}次二分法搜索后, 找到近似解: {x:.6f}，此时函数值为: {bisecSolver.fun(x):.6f}")


if __name__ == '__main__':
    main(-1, 15, 1e-6, 1e-8)

Bisection2roots_promax.py程序运行结果:

                     二分法求解非线性方程数值结果                     
------------------------------------------------------------------
步数			 近似解					 解区间				 函数值
------------------------------------------------------------------
第1步		 7.000000		 [-1.000000, 15.000000]		 0.656987
------------------------------------------------------------------
第2步		 3.000000		 [-1.000000, 7.000000]		 0.141120
------------------------------------------------------------------
第3步		 1.000000		 [-1.000000, 3.000000]		 0.841471
------------------------------------------------------------------
第4步		 0.000000		 [-1.000000, 1.000000]		 0.000000
------------------------------------------------------------------ 

    经判断，第4步达到停止准则: |f[0.000000]| = 0.000000 < ETA
综上，经过4次二分法搜索后, 找到近似解: 0.000000，此时函数值为: 0.000000

bisection_pro.py:

# 开发者:    Leo 刘
# 开发环境: macOs Big Sur
# 开发时间: 2021/9/25 11:39 上午
# 邮箱  : 517093978@qq.com
# @Software: PyCharm
# ----------------------------------------------------------------------------------------------------------
"""
    主函数功能：
    实现改进方法 2（张莉老师提供）的算法思想
    求解在区间$[a,b]$上存在$m$个实根的方程$f(x)=0$.
"""
import numpy as np

import Bisection2roots_promax as Br

import m_roots


# 主函数

def main(a, b, EPS, ETA):
    """

    :param a: 区间左断点
    :param b: 区间右断点
    :param EPS: 近似解的误差限
    :param ETA: 函数值误差限
    """
    print("查看解的分布情况")
    m = m_roots.main(a, b)
    print("\n", "*" * 100, "\n")
    step = (b - a) / m
    a0 = a
    b0 = a0
    roots0 = np.array([])
    bisecSolver = Br.bisectionSolver(a, b, EPS, ETA)
    while bisecSolver.root_counter < m:
        if b0 >= b:
            print("\n", "*" * 100, "\n")
            print(f"搜索步长过大，只找到{bisecSolver.root_counter:d}个(共{m:d}个)近似解，步长减半重新搜索")
            roots0 = np.array([])
            step = step / 2
            a0 = a
            b0 = a0
            bisecSolver.root_counter = 0
        b0 += step
        fa = bisecSolver.fun(a0)
        fb = bisecSolver.fun(b0)
        if fa * fb > 0:
            print("端点函数值计算结果：")
            print("f(a)=%.6f" % fa)
            print("f(b)=%.6f" % fb)
            print("f(a)*f(b)=%.6f" % (fa * fb))
            print("抱歉亲！端点函数值同号，不满足二分法启动条件，已扩大搜索区间重试！")
            continue

        if np.abs(fa) < ETA:
            print("经判断，第%d步达到停止准则: |f(a[%d])| = %.6f < ETA".center(50)
                  % (0, 0, fa))
            bisecSolver.root_counter += 1
            print(f"综上，区间左端点a即为第{bisecSolver.root_counter:d}个(共{m:d}个)近似解: {a0:.6f}，"
                  f"此时函数值为: {bisecSolver.fun(a0):.6f}")
            roots0 = np.append(roots0, a0)
            a0 += (b0 - a0) / 4
            fa = bisecSolver.fun(a0)
            fb = bisecSolver.fun(b0)
            if fa * fb > 0:
                print("端点函数值计算结果：")
                print("f(a)=%.6f" % fa)
                print("f(b)=%.6f" % fb)
                print("f(a)*f(b)=%.6f" % (fa * fb))
                print("抱歉亲！端点函数值同号，不满足二分法启动条件，已扩大搜索区间重试！")
                continue
            (x, n, a_k, b_k) = bisecSolver.bisectionSolver(a0, b0, EPS, ETA)
            print(
                f"综上，经过{n:d}次二分法搜索后, 找到第{bisecSolver.root_counter:d}个(共{m:d}个)近似解: {x:.6f}，"
                f"此时函数值为: {bisecSolver.fun(x):.6f}")
            roots0 = np.append(roots0, x)
            a0 = b0
            b0 = a0
        elif np.abs(fb) < ETA:
            print("经判断，第%d步达到停止准则: |f(b[%d])| = %.6f < ETA".center(50)
                  % (0, 0, fb))
            print(f"综上，区间右端点b即为第{bisecSolver.root_counter:d}个(共{m:d}个)近似解: {b0:.6f}，此时函数值为: {bisecSolver.fun(b0):.6f}")
            roots0 = np.append(roots0, b0)

        else:
            (x, n, a_k, b_k) = bisecSolver.bisectionSolver(a0, b0, EPS, ETA)
            print(
                f"综上，经过{n:d}次二分法搜索后, 找到第{bisecSolver.root_counter:d}个(共{m:d}个)近似解: {x:.6f}，"
                f"此时函数值为: {bisecSolver.fun(x):.6f}")
            roots0 = np.append(roots0, x)
            a0 = b0
            b0 = a0
        for k in range(len(roots0) - 1):
            if roots0[k + 1] - roots0[k] < EPS:
                print("\n", "*" * 100, "\n")
                print(f"两相邻近似解{roots0[k + 1]}与{roots0[k]}可视为同一解，步长减半重新搜索")
                roots0 = np.array([])
                step = step / 2
                a0 = a
                b0 = a0
                bisecSolver.root_counter = 0

    print(f"方程的{m:d}个近似解为：", roots0)


if __name__ == '__main__':
    main(-1, 13, 1e-6, 1e-8)

bisection_pro.py程序运行结果:

查看解的分布情况
--------------------------------------
方程在区间[-1.0000,15.0000]上根的个数为：5
准确解0个，分别为: []
近似解5个，所在区间分别为:
[-0.010000,0.000000]  [3.140000,3.150000]  [6.280000,6.290000]  [9.420000,9.430000]  [12.560000,12.570000]  
 ***********************************************************************

                     二分法求解非线性方程数值结果                     
------------------------------------------------------------------
第4步		 0.000000		 [-0.200000, 0.200000]		 0.000000
------------------------------------------------------------------ 

    经判断，第4步达到停止准则: |f[0.000000]| = 0.000000 < ETA
综上，经过4次二分法搜索后, 找到第1个(共5个)近似解: 0.000000，此时函数值为: 0.000000
                     二分法求解非线性方程数值结果                     
------------------------------------------------------------------
第22步		 3.141593		 [3.141592, 3.141593]		 -0.000000
------------------------------------------------------------------ 

    经判断，第22步达到停止准则: b[22] - a[22] = 0.000001 < EPS
综上，经过22次二分法搜索后, 找到第2个(共5个)近似解: 3.141593，此时函数值为: -0.000000
                     二分法求解非线性方程数值结果                     
------------------------------------------------------------------
第22步		 6.283185		 [6.283185, 6.283186]		 -0.000000
------------------------------------------------------------------ 

    经判断，第22步达到停止准则: b[22] - a[22] = 0.000001 < EPS
综上，经过22次二分法搜索后, 找到第3个(共5个)近似解: 6.283185，此时函数值为: -0.000000
                     二分法求解非线性方程数值结果                     
------------------------------------------------------------------
第22步		 9.424778		 [9.424777, 9.424778]		 0.000000
------------------------------------------------------------------ 

    经判断，第22步达到停止准则: b[22] - a[22] = 0.000001 < EPS
综上，经过22次二分法搜索后, 找到第4个(共5个)近似解: 9.424778，此时函数值为: 0.000000
                     二分法求解非线性方程数值结果                     
------------------------------------------------------------------
第22步		 12.566371		 [12.566370, 12.566371]		 0.000000
------------------------------------------------------------------ 

    经判断，第22步达到停止准则: b[22] - a[22] = 0.000001 < EPS
综上，经过22次二分法搜索后, 找到第5个(共5个)近似解: 12.566371，此时函数值为: 0.000000
方程的5个近似解为： [5.55111512e-17 3.14159279e+00 6.28318520e+00 9.42477760e+00
 1.25663708e+01]

数值分析与算法 - 张莉

图灵猫

关注

2
点赞
踩
3

收藏

觉得还不错? 一键收藏
打赏
0
评论
二分法(Bisection Method)原理及改进

非线性方程的二分法(Bisection Method)文章目录非线性方程的二分法(Bisection Method)条件主要依据主要思想(基本思想)具体过程(方法)优缺点优点缺点改进方法改进方法 1改进方法 2考虑非线性方程f(x)=0f(x)=0f(x)=0条件f(x)∈C[a,b]f(x)\in C[a,b]f(x)∈C[a,b], 且f(a)⋅f(b)<0f(a)·f(b)<0f(a)⋅f(b)<0主要依据由连续函数介值定理,则至少存在某个 x∗∈(a,b)x^* \i
复制链接

扫一扫