速度规划算法解析与实现

速度规划的ST，和路径规划的SL 的S不是一个概念：：

速度规划是沿着路径规划的位移，路径规划是沿着参考线的位移。

ST图的斜率是车辆速度。

 蓝色区域是前车的占据主车路径的行驶区域，宽度是前方车辆占据主车路径的长度（车长），区域斜率是前车速度。

 

 Apollo速度规划算法整体流程：：

task::

（1） 速度边界确定

 为速度规划、运动规划确定ST曲线的边界，蓝色车辆插入主车车道，障碍物出现的区域t，就是出现在主车路径上的时间，S就是障碍车切入主车路径时的位置，

可以加速超过，生成一条区域上面的曲线，

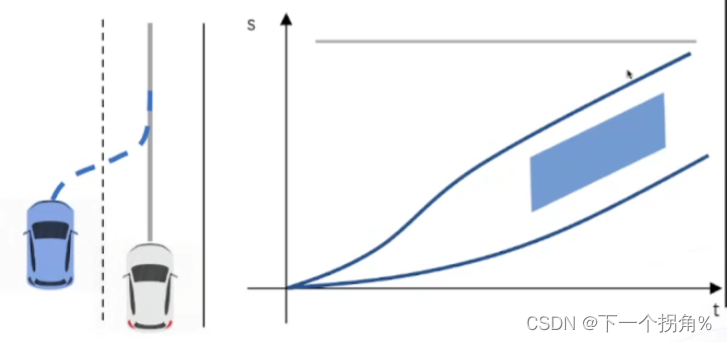
 或者减速让行，生成一条阴影区域下方的曲线。

所以上面产生一个非凸空间，不连续空间，不能采用二次规划，先用动态规划对路径进行一个搜索，确定是让行还是超车（这个怎么确定的？），动态规划会迭代求解一条满足约束的，没有碰撞的路径

（2）速度大致优化

 动态规划的点会比较稀疏

（3）速度决策

 根据粗规划的速度曲线，在障碍物上方还是下方，确定对障碍物超车还是绕行的决策。

（4）速度边界最终决策

 

 （5）速度优化

 上面是非线性速度优化器，主要考虑路径曲率对速度的影响，曲率约束时非线性约束函数。下面是线性速度优化器。配置文件中二选一即可。

（6）合并速度曲线与路径曲线

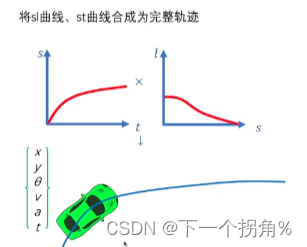
作为最后的 输出

基于动态规划的速度规划

动态规划：：

状态转移方程

把原问题分解为子问题，根据子问题的解求解出原问题的解。 

（1）采样

时间t均匀采样，路径s采用先密后疏采样，提高搜索速度

（2）状态转移方程

 上述是节点的代价

下面是节点之间转移的代价：：速度，加速度，加加速度

 

 

 加速度函数的图像如上。期望一个较小的角速度和角加速度，保证舒适性。

 

总的状态转移方程如上：障碍物、距离、边界的代价，迭代求最小 

基于二次规划的速度规划

 

 ws是位置权重？？，wv是参考速度的权重，pi是根据参考位置制定的一个速度分配，确定一个i时刻速度曲率的权重

上述二次规划的问题：曲率权重pi是一个时间的函数，实际曲率是一个s的函数，即将s的约束转化成了时间约束，如下图，就会曲率约束不精确的问题。

 非线性规划的速度规划

 增加了横向加速度和峰值变量约束

 

要求曲率二次可导

 曲率曲线平滑用的二次规划：：

 

 

 二次规划：：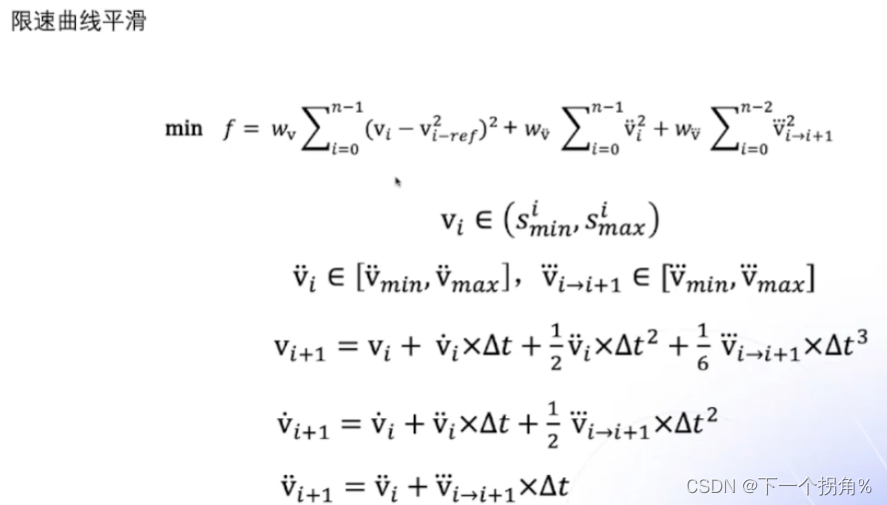

 为了有解并且可导，所以不能像二次规划一样设置硬约束，要设置一定范围波动的软约束：：

 

 可以不限制函数的形式，但是目标约束的函数要二阶可导，

 三个get函数的定义：：

 

 根据二次优化生成一条符合速度约束的速度初始曲线：：作为非线性的初始

eval函数的定义：

为了获得方向需要目标函数的梯度：：梯度

雅可比矩阵：：向量梯度组成的矩阵：：

为了加快求解器的求解速度，只要给出非0元素的位置和值就可以 

 

 

 黑塞矩阵：实值函数所有二阶偏导数组成的矩阵。对拉格朗日函数求黑塞矩阵。

 

 

 算法实践

 

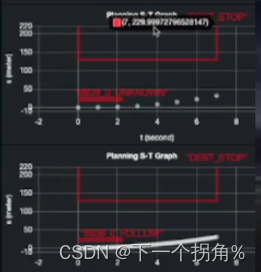
上面是动态规划的ST曲线，下面是非线性规划的ST曲线

打开notebook新建python3时，报错：：