文章目录
参考资料
- 《自动驾驶汽车决策与控制》书籍
本篇博客主要摘抄自书上速度规划这一部分,仅用于学习,方便查阅。
1. 介绍
当局部路径规划给定了一条或者若干条选出的路径曲线之后, 运动规划模块需要解决的后续问题是在此局部路径的基础上加人与速度相关的信息, 这一问题被称为速度规划。
速度规划的目标是在给定的局部路径曲线上, 在满足反馈控制的操作限制及符合行为决策的输出结果这两个前提下, 将路径点赋予速度及加速度信息。速度规划主要考虑的是对动态障碍物的规避。
1.1 常用方法
速度规划有以下常见的方法:
- 对路径指定线加速度来生成速度: 线加速度可以是某一常数, 或是由比例-微分控制器来生成,
- 样条插值: 在给定时间内通过一段给定路径的速度生成问题。其解决方案是将时间域划分为若干区间, 使用速度关于时间的三次样条函数来插值。这一方法容易产生加速度变化率较大的问题。
- 函数拟合: 直接用速度关于路径长度的二次多项式来生成速度。这种方法较为简单。
- 目标时刻点法: 速度规划部分首先根据对障碍物未来运动状态的预测, 在规划路径与时间这两个维度构成的二维图中标记障碍物在未来一段时间内所占据的区域。以目标汽车当前车速匀速通过规划路径所需的时间为基准, 根据一定原则创建一组目标时刻点, 在此二维图中以目标时刻点为目标点搜索产生一组速度规划方案。
- QP算法: 这一方法引人了S-T图的概念,并把自动驾驶汽车速度规划归纳为S-T图上的搜索问题进行求解。S-T图是一个关于给定局部路径纵向位移和时间的二维关系图。任何一个S-T图都基于一条已经给定的轨迹曲线。根据自动驾驶汽车预测模块对动态障碍物的轨迹预测,每个动态障碍物都会在这条给定的路径上有投影, 从而产生对于一定S-T区域的覆盖。
2. QP算法
下面详解QP算法进行速度规划。
2.1 障碍物预测
当环境中出现移动障碍的时候, 移动障碍会在末来某些时刻 ( t 1 、 t 2 、 t 3 ) \left(t_{1} 、 t_{2} 、 t_{3}\right) (t1、t2、t3) 占据已经规划好的路径。如果目标汽车仍然以当前车速匀速行驶, 有可能会在末来的某一时刻与移动障碍 相碰撞。
根据移动障碍当前所处位置
(
x
0
o
b
j
,
y
0
o
b
j
)
\left(x_{0_{o b j}}, y_{0_{o b j}}\right)
(x0obj,y0obj) 、速度
(
v
0
o
b
j
,
v
0
o
b
j
)
\left(v_{0_{o b j}}, v_{0_{o b j}}\right)
(v0obj,v0obj) 、加速度
(
a
0
o
b
j
,
a
0
o
b
j
)
\left(a_{0_{o b j}}, a_{0_{o b j}}\right)
(a0obj,a0obj), 可以预 测经过时间
t
t
t 后移动障碍所处位置
(
x
t
o
b
j
,
y
t
o
b
j
)
\left(x_{t_{\mathrm{obj}}}, y_{t_{\mathrm{obj}}}\right)
(xtobj,ytobj) :
{
x
t
o
b
j
=
x
0
o
b
j
+
v
x
o
b
j
×
t
+
1
2
×
a
x
o
b
j
×
t
2
y
t
o
b
j
=
y
0
o
b
j
+
v
y
o
b
j
×
t
+
1
2
×
a
y
o
b
j
×
t
2
\left\{\begin{array}{l} x_{t_{\mathrm{obj}}}=x_{0_{\mathrm{obj}}}+v x_{\mathrm{obj}} \times t+\frac{1}{2} \times a x_{\mathrm{obj}} \times t^{2} \\ y_{t_{\mathrm{obj}}}=y_{0_{\mathrm{obj}}}+v y_{\mathrm{obj}} \times t+\frac{1}{2} \times a y_{\mathrm{obj}} \times t^{2} \end{array}\right.
{xtobj=x0obj+vxobj×t+21×axobj×t2ytobj=y0obj+vyobj×t+21×ayobj×t2
用矩阵表示为:
Y
=
[
x
t
o
b
j
y
t
o
b
j
]
,
X
=
[
1
t
t
2
]
,
A
=
[
x
0
o
b
j
v
x
o
b
j
1
2
a
x
o
b
j
y
0
o
b
j
v
y
o
b
j
1
2
a
y
o
b
j
]
Y
=
A
X
\boldsymbol{Y}=\left[\begin{array}{l} x_{t_{o b j}} \\ y_{t_{o b j}} \end{array}\right], \quad \boldsymbol{X}=\left[\begin{array}{c} 1 \\ t \\ t^{2} \end{array}\right], \quad \boldsymbol{A}=\left[\begin{array}{ccc} x_{0_{o b j}} & v x_{\mathrm{obj}} & \frac{1}{2} a x_{\mathrm{obj}} \\ y_{0_{\mathrm{obj}}} & v y_{\mathrm{obj}} & \frac{1}{2} a y_{\mathrm{obj}} \end{array}\right] \\ \\ Y=AX
Y=[xtobjytobj],X=⎣
⎡1tt2⎦
⎤,A=[x0objy0objvxobjvyobj21axobj21ayobj]Y=AX
得到
t
t
t 时刻移动障碍所处位置
Y
\boldsymbol{Y}
Y 后, 根据移动障 碍轮廓计算其覆盖区域
Q
Q
Q :
Y
⇒
Q
Y \Rightarrow Q
Y⇒Q
图
4.23
4.23
4.23 所示为障碍物覆盖区域与规划轨迹的交集示意图。

计算
Q
Q
Q 与规划路径
S
S
S 的交集
Δ
S
\Delta S
ΔS :
Δ
S
=
Q
∩
S
\Delta S=Q \cap S
ΔS=Q∩S
那么,
Δ
S
\Delta S
ΔS 与
t
t
t 一一对应。
2.2 S-T图生成
S-T图是已经规划完成的路径纵向位移与时间之间的二维关系图(见图4.24)。前面已经获得 Δ S \Delta S ΔS关于 t t t的信息, 那么可以在S-T图中标记某一时刻t在路径S上占据的某一段路径 Δ S \Delta S ΔS。如图4.24所示,假如移动障碍物经过了规划路径, 那么因为移动障碍物在一段时间内占据了规划路径, 在S-T图中将会有一块覆盖区域。

图 4.24 4.24 4.24 中 S goal S_{\text {goal }} Sgoal 为规划路径的长度。虚线代表的是目标汽车以当前车速匀速沿规划路 径行驶, 用时记为 t a t_{a} ta 。可以发现在某些时刻目标汽车和移动障碍将会同时出现在期望路径 的某一位置, 这意味着目标汽车将与移动障碍碰撞。实线代表的是目标汽车从当前时刻开始以最大加速度加速通过期望路径, 用时记为 t min t_{\text {min }} tmin 。
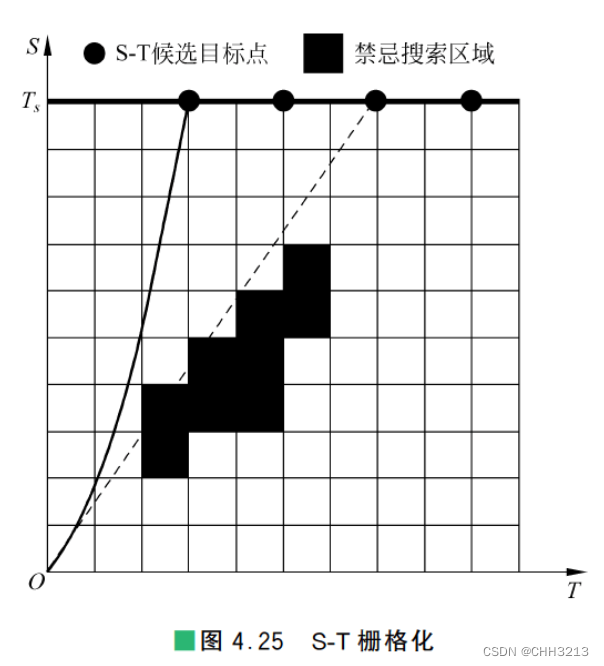
2.3 S-T 图栅格化
对 S-T 图栅格化。为了有利于在 S-T 图中进行路径搜索, 需要对 S-T 图进行离散化、 网格化。根据需要确定采样周期和规划路径的路径点间隔, 如图 4.25 4.25 4.25 所示。
从当前时刻开始根据采样周期针对末来某一时刻 t k t_{k} tk 计算移动障碍所处位置 Y k \boldsymbol{Y}_{k} Yk, 其中 k k k 为 1 ∼ c 1 \sim c 1∼c 的自然数, c c c 的值根据移动障碍离开规划路径的时刻确定。 t k t_{k} tk 与 t k + 1 t_{k+1} tk+1 之间的时间差为采样周期。
X
k
=
[
1
t
k
t
k
2
]
,
Y
k
=
[
x
t
k
y
t
k
]
,
k
∈
(
1
,
c
)
且
k
∈
N
Y
k
=
A
X
k
Y
k
⇒
Q
k
Δ
S
k
=
Q
k
∩
S
x
y
\begin{aligned} &\boldsymbol{X}_{k}=\left[\begin{array}{c} 1 \\ t_{k} \\ t_{k}^{2} \end{array}\right], \quad \boldsymbol{Y}_{k}=\left[\begin{array}{l} x_{t_{k}} \\ y_{t_{k}} \end{array}\right], \quad k \in(1, c) \text { 且 } k \in \mathbf{N} \\ &\boldsymbol{Y}_{k}=\boldsymbol{A} \boldsymbol{X}_{k} \\ &\boldsymbol{Y}_{k} \Rightarrow Q_{k} \\ &\Delta S_{k}=Q_{k} \cap S_{x y} \end{aligned}
Xk=⎣
⎡1tktk2⎦
⎤,Yk=[xtkytk],k∈(1,c) 且 k∈NYk=AXkYk⇒QkΔSk=Qk∩Sxy
最终得到
Δ
S
k
,
Δ
S
k
\Delta S_{k}, \Delta S_{k}
ΔSk,ΔSk 中包含在时刻
t
k
t k
tk 移动障碍物在采样后的期望路径点上的投影。将
t
k
t k
tk 与
Δ
S
k
\Delta S_{k}
ΔSk 相对应的标记在网格化后的
S
−
T
\mathrm{S}-\mathrm{T}
S−T 图上, 此即为
S
−
T
\mathrm{S}-\mathrm{T}
S−T 搜索图。
2.4 创建目标时刻点
创建 S − T \mathrm{S}-\mathrm{T} S−T 搜索图的目的在于为搜索算法提供搜索空间。从 t a t_{a} ta 与 t min t_{\min } tmin 中选择较小的值 记为 T t min T_{t_{\text {min }}} Ttmin , 从 T t min T_{t_{\text {min }}} Ttmin 开始向后等间隔产生一组时刻点, 这些时刻点(包括 T t min T_{t_{\text {min }}} Ttmin ) 用 T t r ( r ∈ N T_{t_{r}}(r \in \mathbf{N} Ttr(r∈N 且 r ≠ 0 ) r \neq 0) r=0) 表示, 数目由移动障碍在 S − T \mathrm{S}-\mathrm{T} S−T 图中占据的区域而定。 T t r T_{t_{r}} Ttr 被称为目标时刻, T t r T_{t_{r}} Ttr 的 集合记为 T T , T T T_{T}, T_{T} TT,TT 被称为目标时刻集。同时产生与之数量相匹配的一组 T s r , T s r T_{s_{r}}, T_{s_{r}} Tsr,Tsr 的大小与 S goal S_{\text {goal }} Sgoal 相等, 被称为目标路径点, 这一组 T s r T_{s_{r}} Tsr 的集合记为 T S T_{S} TS, 称为目标路径点集。 T T T_{T} TT 与 T S T_{S} TS 中的元素一一对应, 并且对应了 S − T \mathrm{S}-\mathrm{T} S−T 图上 T S T_{S} TS 线上的一组点, 这组点称为目标时刻点。
2.5 搜索产生路径
结合上游行为决策输出的信息, 速度规划可以灵活设置障碍物体周边的代价 (Cost), 达 到调整速度方案的目的。当上游决定针对物体 a 进行抢先决策时, 在 S − T \mathrm{S}-\mathrm{T} S−T 图上物体 a \mathrm{a} a 运动路径上方的网格的 Cost 就可以调成偏小。同时, 为了避免任何潜在的碰撞, 所有动态障碍物的路径经过的网格的 Cost 都需要调大。
除此之外, 还需要考虑一条给定速度方案在加速度等方面的 Cost。例如, S-T 图上过于 “陡峭”的曲线代表加速度大甚至不连续, 这样很有可能导致反馈控制模块 (Feedback Control)无法实际执行。所以, 每条曲线所对应的速度方案均有一个整体的 Cost。实际上, 根据上游 (决策) 输出和下游 (控制) 限制来调整 Cost, 是速度规划中的 S-T 图算法的关键设 置。在设置好 Cost 的基础上, 最小 Cost 局部路径的产生可以用类似 A ∗ \mathrm{A}^{*} A∗ 或者 Dijkstra 等简 单搜索算法实现。在得到了最小 Cost 的 S − T \mathrm{S}-\mathrm{T} S−T 路径后,可以简单算出局部路径上任何一个位 置对应的速度 (对应 S-T 图任意点斜率) 和加速度 (斜率的导数), 从而完成速度规划的计算。
基于路径搜索算法针对每一个 S-T 候选目标点,在 S-T 禁忌搜索空间中搜索产生从起 点到目标点的路径, 如图 4.26 所示。

2.6 速度平滑
通过路径搜索算法在S-T禁忌搜索图中找到一条从起点到目标点的路径的时候, 由于对原有 S-T图的离散采样, 所以得到的路径也是曲折且离散的。为了获得平滑的路径曲线, 可以利用多项式回归分析对离散路径点进行拟合, 此外, QP 算法同样可应用于速度平滑过程中。
多项式回归在速度平滑中的应用。
速度规划中通过路径搜索产生的路径点数量巨大, 而且对计算机计算时间也有要求, 所 以对速度规划路径点进行回归分析通过迭代寻优的方式完成。以基于 5 次曲线的多项式为 例, 对其对应 5 次多项式的系数进行迭代寻优, 从而获取平滑后的速度曲线。
在对 S-T 图中的路径点进行 5 次曲线拟合得到速度规划方案时, 需要考虑目标汽车在 t t t 为 0 时当前时刻目标汽车的速度值和加速度值以及 S-T 图中创建的目标时刻点。也就是说利用 5 次曲线对 S-T 图中速度规划路径点的拟合, 是一个包含等式约束的优化问题。
当通过路径搜索算法在 S-T 图中搜索产生路径后, 可以获取一组路径点
(
t
i
,
s
i
)
(
i
=
0
\left(t_{i}, s_{i}\right)(i=0
(ti,si)(i=0,
1
,
2
,
⋯
,
m
)
1,2, \cdots, m)
1,2,⋯,m) 。用于速度规划路径点的 5 次拟合函数为:
s
(
t
)
=
k
0
+
k
1
t
+
k
2
t
2
+
k
3
t
3
+
k
4
t
4
+
k
5
t
5
s(t)=k_{0}+k_{1} t+k_{2} t^{2}+k_{3} t^{3}+k_{4} t^{4}+k_{5} t^{5}
s(t)=k0+k1t+k2t2+k3t3+k4t4+k5t5
由此可以构建损失函数:
J
(
k
0
,
k
1
,
k
2
,
k
3
,
k
4
,
k
5
)
=
1
2
m
∑
i
=
1
m
(
h
k
(
t
i
)
−
s
i
)
2
J\left(k_{0}, k_{1}, k_{2}, k_{3}, k_{4}, k_{5}\right)=\frac{1}{2 m} \sum_{i=1}^{m}\left(h_{k}\left(t_{i}\right)-s_{i}\right)^{2}
J(k0,k1,k2,k3,k4,k5)=2m1i=1∑m(hk(ti)−si)2
在速度规划中, 目标汽车在轨迹上所处的位置用
s
s
s 表示, 速度用
s
′
s^{\prime}
s′ 表示, 加速度用
s
′
′
s^{\prime \prime}
s′′ 表 示, 则在时刻
t
t
t, 目标汽车的车速为:
s
′
(
t
)
=
k
1
+
2
k
2
t
+
3
k
3
t
2
+
4
k
4
t
3
+
5
k
5
t
4
s^{\prime}(t)=k_{1}+2 k_{2} t+3 k_{3} t^{2}+4 k_{4} t^{3}+5 k_{5} t^{4}
s′(t)=k1+2k2t+3k3t2+4k4t3+5k5t4
目标汽车加速度为:
s
′
′
(
t
)
=
2
k
2
+
6
k
3
t
+
12
k
4
t
2
+
20
k
5
t
3
s^{\prime \prime}(t)=2 k_{2}+6 k_{3} t+12 k_{4} t^{2}+20 k_{5} t^{3}
s′′(t)=2k2+6k3t+12k4t2+20k5t3
已知
t
=
0
t=0
t=0 时初始状态下目标汽车在规划轨迹上所处位置、汽车速度、汽车加速度为已 知量, 即
s
(
0
)
=
k
0
=
s
t
=
0
s
′
(
0
)
=
k
1
=
s
t
=
0
′
s
′
′
(
0
)
=
2
k
2
=
s
t
=
0
′
′
\begin{aligned} &s(0)=k_{0}=s_{t=0} \\ &s^{\prime}(0)=k_{1}=s_{t=0}^{\prime} \\ &s^{\prime \prime}(0)=2 k_{2}=s_{t=0}^{\prime \prime} \end{aligned}
s(0)=k0=st=0s′(0)=k1=st=0′s′′(0)=2k2=st=0′′
并且可以知道目标时刻点信息, 即存在
s
(
t
r
)
=
k
0
+
k
1
t
r
+
k
2
t
r
2
+
k
3
t
r
3
+
k
4
t
r
4
+
k
5
t
r
5
=
s
t
s\left(t_{r}\right)=k_{0}+k_{1} t_{r}+k_{2} t_{r}^{2}+k_{3} t_{r}^{3}+k_{4} t_{r}^{4}+k_{5} t_{r}^{5}=s_{t}
s(tr)=k0+k1tr+k2tr2+k3tr3+k4tr4+k5tr5=st
那么联立可得 :
{
k
0
=
s
t
=
0
k
1
=
s
t
=
0
′
k
2
=
1
2
s
t
=
0
′
′
k
3
=
s
t
t
r
3
−
s
t
=
0
t
r
3
−
s
t
=
0
′
t
r
2
−
s
t
=
0
′
′
2
t
r
−
k
4
t
r
−
k
5
t
r
2
\left\{\begin{array}{l} k_{0}=s_{t=0} \\ k_{1}=s_{t=0}^{\prime} \\ k_{2}=\frac{1}{2} s_{t=0}^{\prime \prime} \\ k_{3}=\frac{s_{t}}{t_{r}^{3}}-\frac{s_{t=0}}{t_{r}^{3}}-\frac{s_{t=0}^{\prime}}{t_{r}^{2}}-\frac{s_{t=0}^{\prime \prime}}{2 t_{r}}-k_{4} t_{r}-k_{5} t_{r}^{2} \end{array}\right.
⎩
⎨
⎧k0=st=0k1=st=0′k2=21st=0′′k3=tr3st−tr3st=0−tr2st=0′−2trst=0′′−k4tr−k5tr2
损失函数可以表示为仅关于
k
4
,
k
5
k_{4}, k_{5}
k4,k5 的表达式, 即
J
(
k
4
,
k
5
)
=
1
2
m
∑
i
=
1
m
(
h
k
(
t
i
)
−
s
i
)
2
J\left(k_{4}, k_{5}\right)=\frac{1}{2 m} \sum_{i=1}^{m}\left(h_{k}\left(t_{i}\right)-s_{i}\right)^{2}
J(k4,k5)=2m1i=1∑m(hk(ti)−si)2
则
k
4
,
k
5
k_{4}, k_{5}
k4,k5 的梯度分别为:
∂
∂
k
4
J
(
k
4
,
k
5
)
=
∂
∂
k
4
1
2
m
∑
i
=
1
m
(
h
k
(
t
i
)
−
s
i
)
2
=
1
m
1
2
m
∑
i
=
1
m
[
(
h
k
(
t
i
)
−
s
i
)
(
t
i
4
−
t
r
t
i
3
)
]
\frac{\partial}{\partial k_{4}} J\left(k_{4}, k_{5}\right)=\frac{\partial}{\partial k_{4}} \frac{1}{2 m} \sum_{i=1}^{m}\left(h_{k}\left(t_{i}\right)-s_{i}\right)^{2}=\frac{1}{m} \frac{1}{2 m} \sum_{i=1}^{m}\left[\left(h_{k}\left(t_{i}\right)-s_{i}\right)\left(t_{i}^{4}-t_{r} t_{i}^{3}\right)\right]
∂k4∂J(k4,k5)=∂k4∂2m1i=1∑m(hk(ti)−si)2=m12m1i=1∑m[(hk(ti)−si)(ti4−trti3)]
∂
∂
k
5
J
(
k
4
,
k
5
)
=
∂
∂
k
5
1
2
m
∑
i
=
1
m
(
h
k
(
t
i
)
−
s
i
)
2
=
1
m
1
2
m
∑
i
=
1
m
[
(
h
k
(
t
i
)
−
s
i
)
(
t
i
5
−
t
r
2
t
i
3
)
]
\frac{\partial}{\partial k_{5}} J\left(k_{4}, k_{5}\right)=\frac{\partial}{\partial k_{5}} \frac{1}{2 m} \sum_{i=1}^{m}\left(h_{k}\left(t_{i}\right)-s_{i}\right)^{2}=\frac{1}{m} \frac{1}{2 m} \sum_{i=1}^{m}\left[\left(h_{k}\left(t_{i}\right)-s_{i}\right)\left(t_{i}^{5}-t_{r}^{2} t_{i}^{3}\right)\right]
∂k5∂J(k4,k5)=∂k5∂2m1i=1∑m(hk(ti)−si)2=m12m1i=1∑m[(hk(ti)−si)(ti5−tr2ti3)]
梯度下降寻优的过程就是不断更新
k
4
,
k
5
k_{4}, k_{5}
k4,k5 。
求最小损失函数值的过程:
k
4
=
k
4
+
α
1
m
∑
i
=
1
m
[
(
h
k
(
t
i
)
−
s
i
)
(
t
i
4
−
t
r
t
i
3
)
]
k
5
=
k
5
+
α
1
m
∑
i
=
1
m
[
(
h
k
(
t
i
)
−
s
i
)
(
t
i
5
−
t
r
t
i
3
)
]
\begin{aligned} k_{4} &=k_{4}+\alpha \frac{1}{m} \sum_{i=1}^{m}\left[\left(h_{k}\left(t_{i}\right)-s_{i}\right)\left(t_{i}^{4}-t_{r} t_{i}^{3}\right)\right] \\ k_{5} &=k_{5}+\alpha \frac{1}{m} \sum_{i=1}^{m}\left[\left(h_{k}\left(t_{i}\right)-s_{i}\right)\left(t_{i}^{5}-t_{r} t_{i}^{3}\right)\right] \end{aligned}
k4k5=k4+αm1i=1∑m[(hk(ti)−si)(ti4−trti3)]=k5+αm1i=1∑m[(hk(ti)−si)(ti5−trti3)]
当损失函数值收敛于允许误差之内时, 认为找到最优解, 此时得到的
k
4
,
k
5
k_{4}, k_{5}
k4,k5 可以最终确 定对给定的路径点拟合程度最好的拟合函数方程。

























 2386
2386

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










