第二节 控制系统的数学模型——传递函数

博客已搬家，欢迎访问新居：http://lukeyalvin.site，主要涉及SLAM相关方向，目前知识积累尚浅，多多指教！

第二节 控制系统的数学模型——传递函数

了解数学模型的概念，自动控制原理都包含哪些数学模型，怎样将系统转换为数学模型

什么是控制系统的数学模型？控制系统的模型有哪些种？

数学模型是用来描述系统因果关系的数学表达式。有微分方程、传递函数、结构框图、信号流图、频率特性、差分方程、状态方程、传递矩阵等表达形式。

什么是控制系统的数学模型？控制系统的模型有哪些种？

数学模型是用来描述系统因果关系的数学表达式。有微分方程、传递函数、结构框图、信号流图、频率特性、差分方程、状态方程、传递矩阵等表达形式。

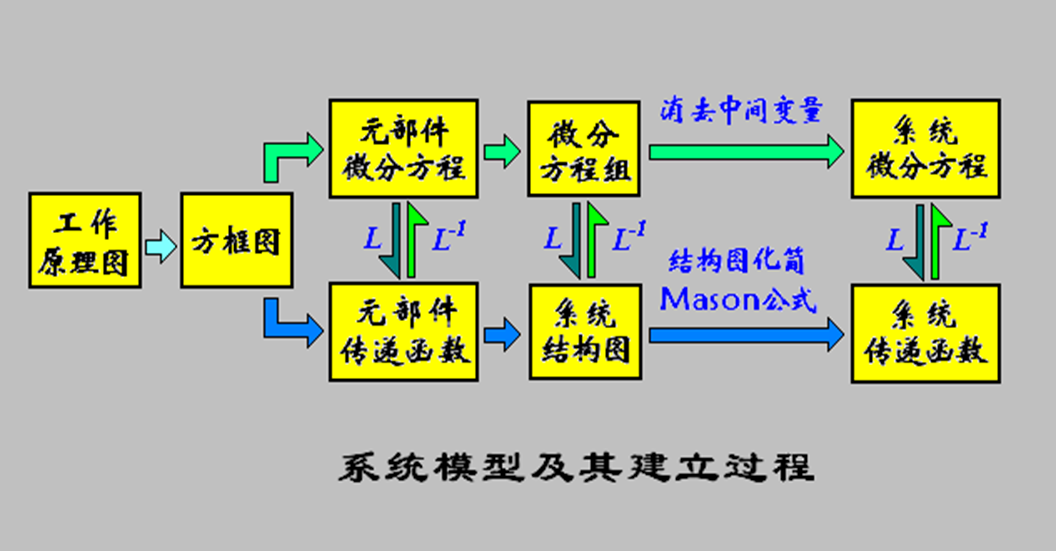
系统数学模型建立的过程：

微分方程

RLC电路微分方程的建立（二阶）

$$\begin{gathered} u_r(t)=L\frac{d_i(t)}{dt}+R_i(t)+u_c(t) \\ i(t)=C\frac{d{u}_c(t)}{dt} \\ {u}_r(t)=LC\frac{d^2{u}_c(t)}{d{t}^2}+RC\frac{d{u}_c(t)}{dt}+ \end{gathered}$$