一种体渲染方法:从3D物体到2D平面
3DGS和Nerf区别:
Nerf
Ray-casting是被动的:计算每个像素点受到发光粒子的影响来生成图像。
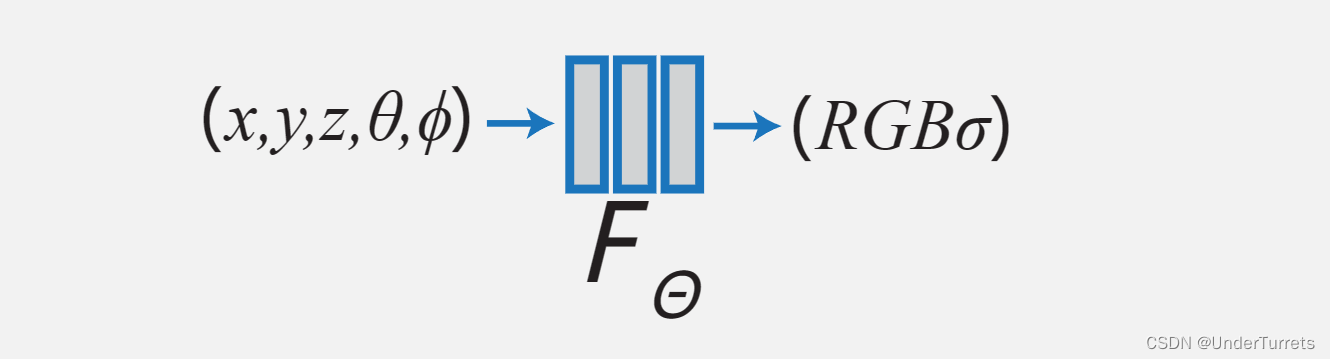
NeRF利用多层感知机(MLP)创建了一个函数。函数接受一个向量 (x,y,z,θ,ϕ)作为输入,其中,(x,y,z) 表示这个点在空间中的坐标,(θ,ϕ)表示观察角度(俯仰角pitch和偏航角yaw)。它的输出是 (RGB,σ)。其中 σ,是一个被称为体素密度的计算量。
有了体素密度之后进行渲染,NeRF的渲染方式采用经典的体渲染。需要三个参数作为输入:
- 目标位姿
- 空间中每个位置的体素密度
- 空间中每个位置的RGB颜色值
然后输出:
- 目标位姿对应的图片
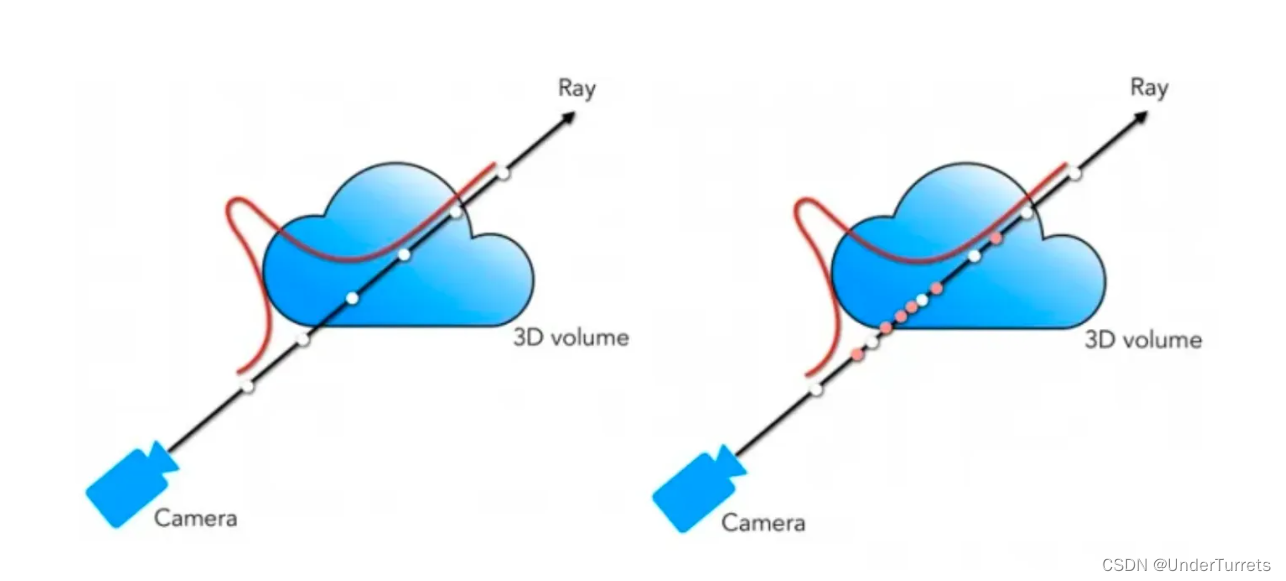
这种体渲染的方式需要以像素为单位生成光线,然后在光线上对空间内的点进行采样,因此,每个像素点在渲染时都需要计算对应的光线,成本相当高昂,在渲染高分辨率图像时帧率非常低下,无法做到实时渲染。
同样基于这个原因,NeRF优化参数时,在源图像与生成图像上只会选择一些像素点,去计算RGB颜色值的损失,进行反向传播,优化MLP的参数,而不是将所有像素点都拿来计算损失。
3DGS splatting(基于2001年EWA Volume Splatting+1990年Splatting)
Splatting是主动的:计算出每个发光粒子如何影响像素点
3DGS首先将空间中的3D高斯投影到基于像素的图像平面上,这个过程被称为泼溅(splatting)。随后,3DGS对这些高斯进行排序并计算每个像素的值。
核心:Splatting(形象解释“抛雪球”)
1、选择“雪球”
2、抛掷雪球:3D to 2D,得到足迹
3、合成,形成图像

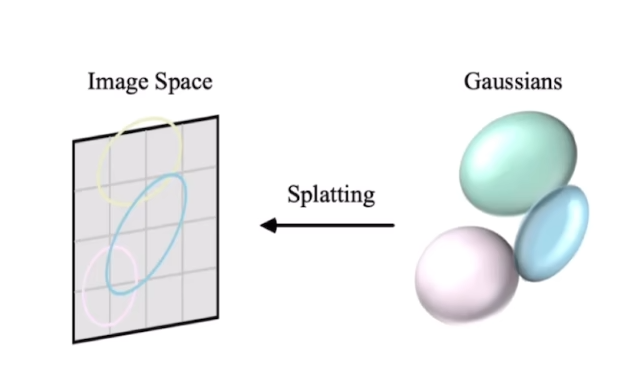
为什么使用核(雪球)?
- 点没有体积,没有能量,对他进行膨胀
- 高斯/圆/正方体/圆柱体
为什么选择3DGS作为“雪球”?
- 仿射变换后高斯核仍然闭合,还是一个高斯
- 沿着某一个轴积分,3D降维到2D仍然是高斯
3DGS splatting
3D gaussian
 ,
,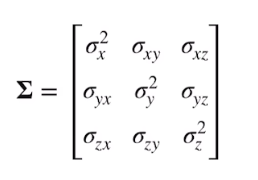
算出来是个概率?为什么可以是一个椭球?
变量只在指数上,现在假设多维时候GS值为常量,变量表示的是什么形状
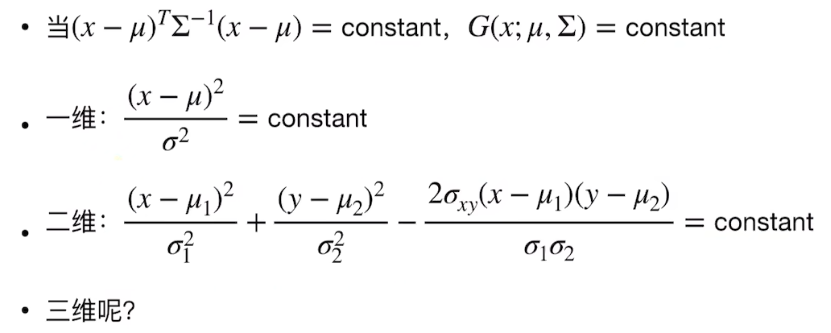
三维:椭球面(x在这里为三维,分别与对于的均值、方差对应起来)
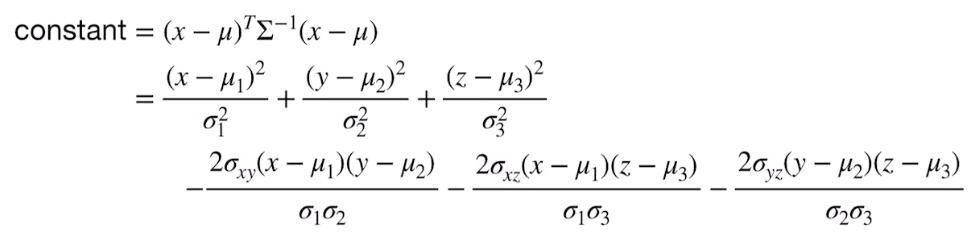
现在取消对高斯为一个常量的假设
G ( x ; u , Σ ) = [ 0 , 1 ] G(x;u,\Sigma)= [0,1] G(x;u,Σ)=[0,1] 概率,结果是一个实心椭球

GS的性质:
| 各项同性: | 各项异性: |
|---|---|
| + 在所有方向具有相同的扩散程度(梯度) + 球 + 3DGS分布:协方差矩阵是对角阵 + 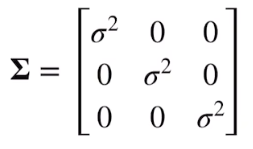 | + 在不同方向具有不同的扩散程度(梯度) + 椭球 + 3DGS分布:协方差矩阵是对角阵 + 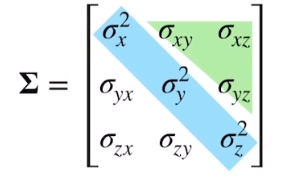 |
 |  |
| 标准的高斯分布: | 高斯分布: |
| x ∼ N ( 0 ⃗ , 1 ) x{\sim}N(\vec{0},1) x∼N(0,1) | x ∼ N ( μ , Σ ) x{\sim}N(\mu,\Sigma) x∼N(μ,Σ) |
| 均值[0, 0, 0] | 均值 [ μ 1 , μ 2 , μ 3 ] [\mu_{1}, \mu_{2}, \mu_{3}] [μ1,μ2,μ3] |
 |  |
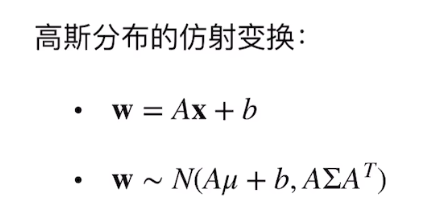 于是:任意高斯可以是由标准高斯通过仿射变换得到 |
协方差矩阵和旋转和缩放之间的转换
在仿射变换中,包含旋转(R),缩放(S),平移(b)
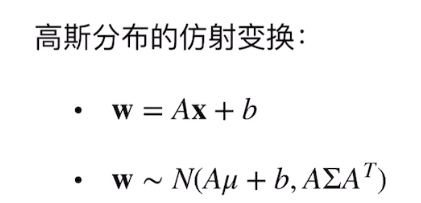
根据概念
A
=
R
S
A=RS
A=RS
b
b
b表示平移**
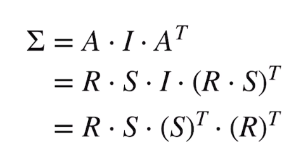
这里,协方差矩阵就被表示为旋转和缩放的形式
若已知协方差矩阵,求R、S。 Σ = Q Λ Q T = Q Λ 1 / 2 Λ 1 / 2 Q T \Sigma = Q{\Lambda}Q^{T} = Q{\Lambda^{1/2}\Lambda^{1/2}}Q^{T} Σ=QΛQT=QΛ1/2Λ1/2QT
协方差矩阵控制形状,R、S控制协方差。
3D到像素变换过程
Nerf: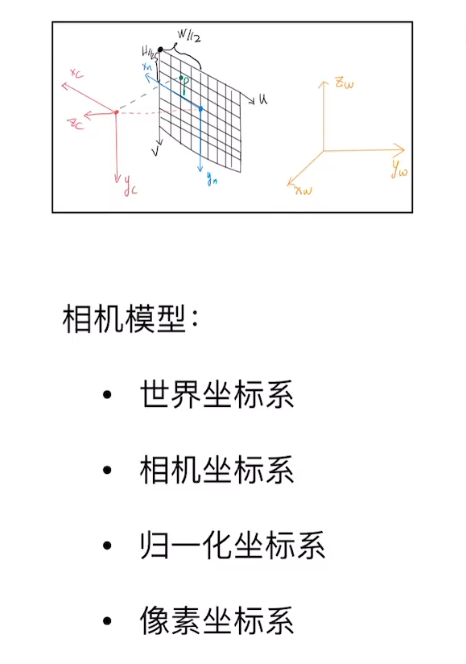 | CG: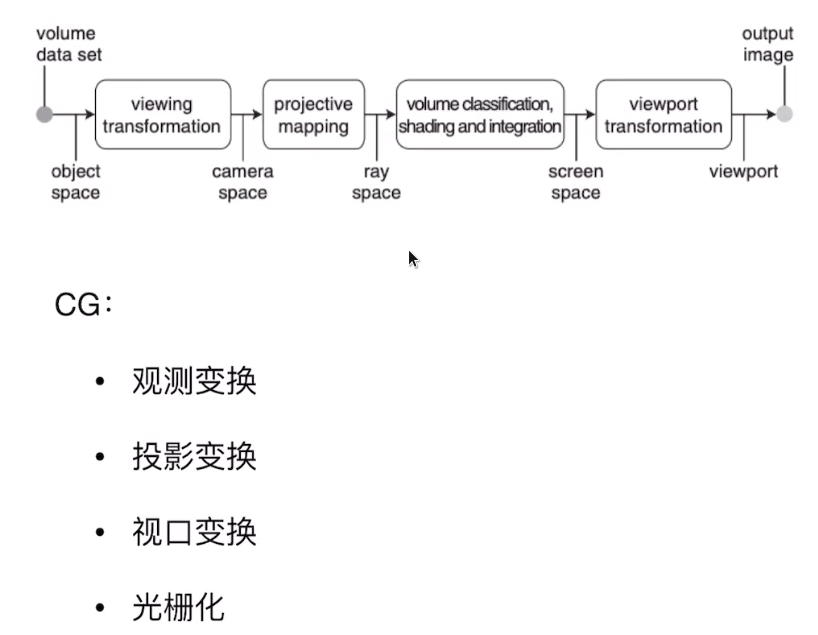 |
|---|
观测变换
通过仿射变换,从世界坐标系到相机坐标系的转换。 w = A x + b w = Ax +b w=Ax+b
投影变换
- 3D到2D
- 透视投影,与z轴相关
- 正交投影,与z轴无关
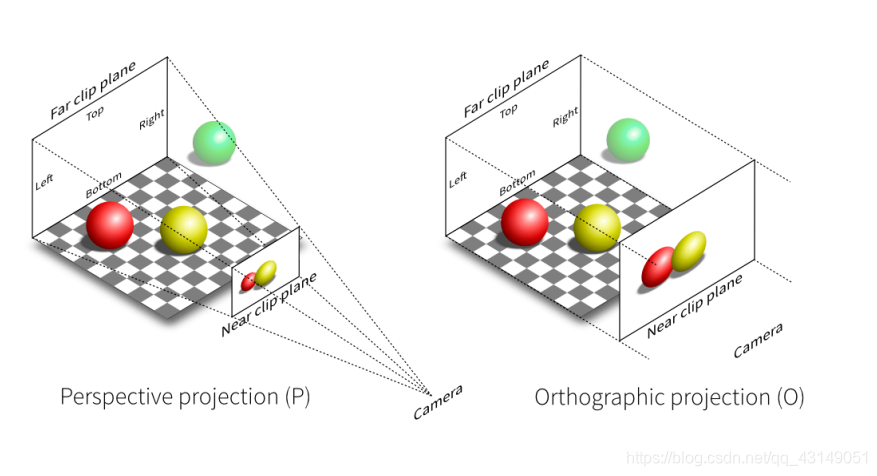
1、正交投影
- 将立方体 [ l , r ] × [ b , t ] × [ f , n ] [l,r]\times[b,t]\times[f,n] [l,r]×[b,t]×[f,n]平移到原点
- 缩放到 [ − 1 , 1 ] 3 [-1,1]^{3} [−1,1]3的正方体中
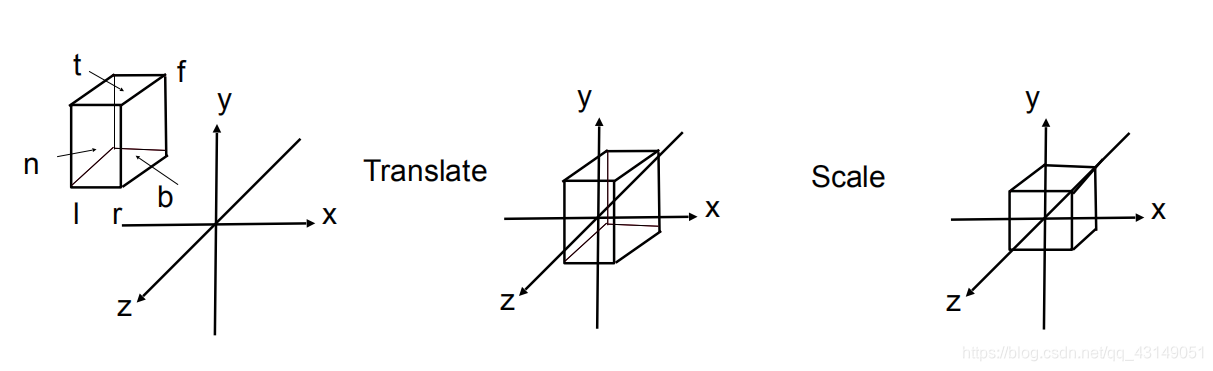
通过仿射变换完成正交投影
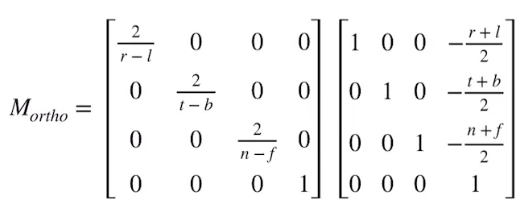
2、透视变换
- 远小近大
- 先把椎体“压”成立方体
- 再正交投影
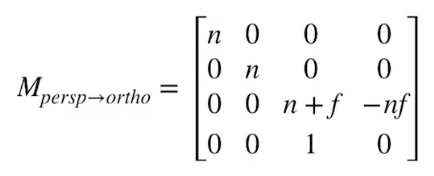
M p e r s p = M o r t h M p e r s p → o r t h o M_{persp}=M_{orth}M_{persp{\rightarrow}ortho} Mpersp=MorthMpersp→ortho
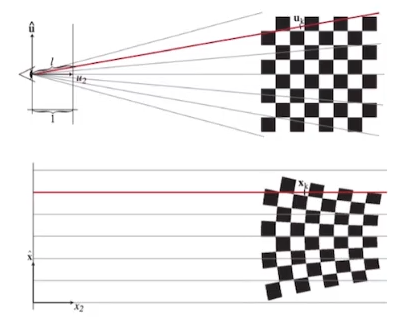
- 透视变换是非线性的,非仿射变换
- 希望高斯椭一直进行仿射变换
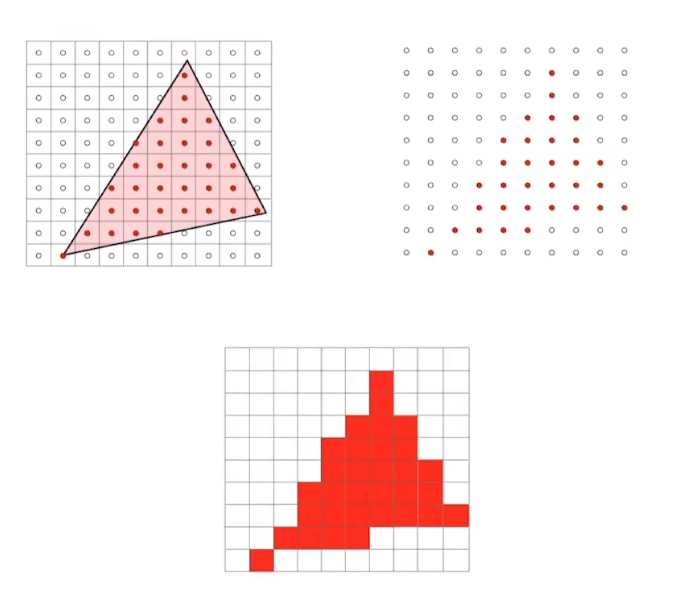
视口变换
- 与z无关
- 将 [ − 1 , 1 ] 2 [-1,1]^2 [−1,1]2的矩形变换至 [ 0 , w ] × [ 0 , h ] [0,w]\times[0,h] [0,w]×[0,h]
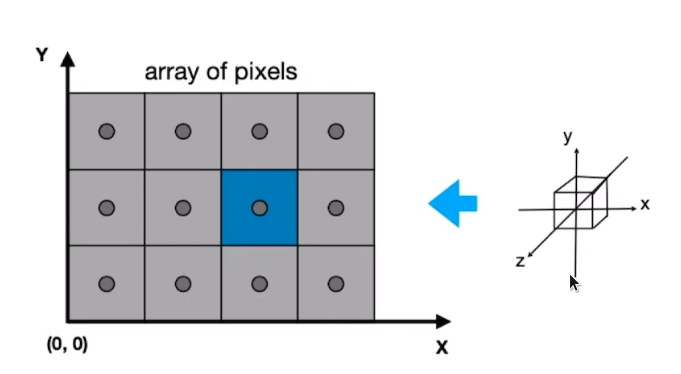
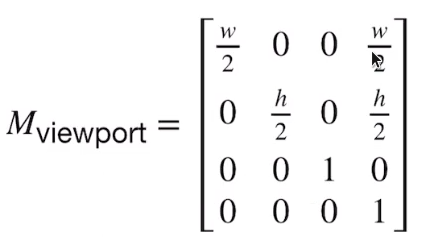
光栅化
- 把东西画在屏幕上
- 连续转离散
- 使用的方法:采样
3DGS到像素变换
GS观测变换



GS投影变换
在这里不能直接使用上述的投影变换:
- 从透视投影到正交投影是非线性变换,非仿射
解决办法:
- 引入雅可比近似矩阵(3D GS中心点附近做雅可比矩阵近似为线性变换)
| 观测变换 | 线性近似的投影变换 |
|---|---|
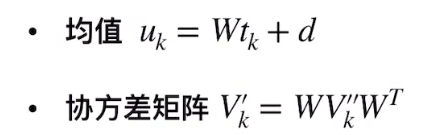 |  |
| 再加上世界坐标系到相机坐标系的观测变换: V k = J V k ′ J T = J W V k ′ ′ W T J T V_{k} = J V^{'}_{k}J^{T} = JW V^{''}_{k}W{T}J^{T} Vk=JVk′JT=JWVk′′WTJT  | |
| 均值: 1、 在正交坐标系 2、 范围 [ − 1 , 1 ] 3 [-1,1]^3 [−1,1]3 协方差矩阵: 1、 在为缩放的正交坐标系 2、 范围 [ l , r ] × [ b , t ] × [ f , n ] [l,r]\times[b,t]\times[f,n] [l,r]×[b,t]×[f,n] 疑问: 为什么这里均值要视口变换 协方差矩阵不用视口变换 |
这里从普通投影变换推导:
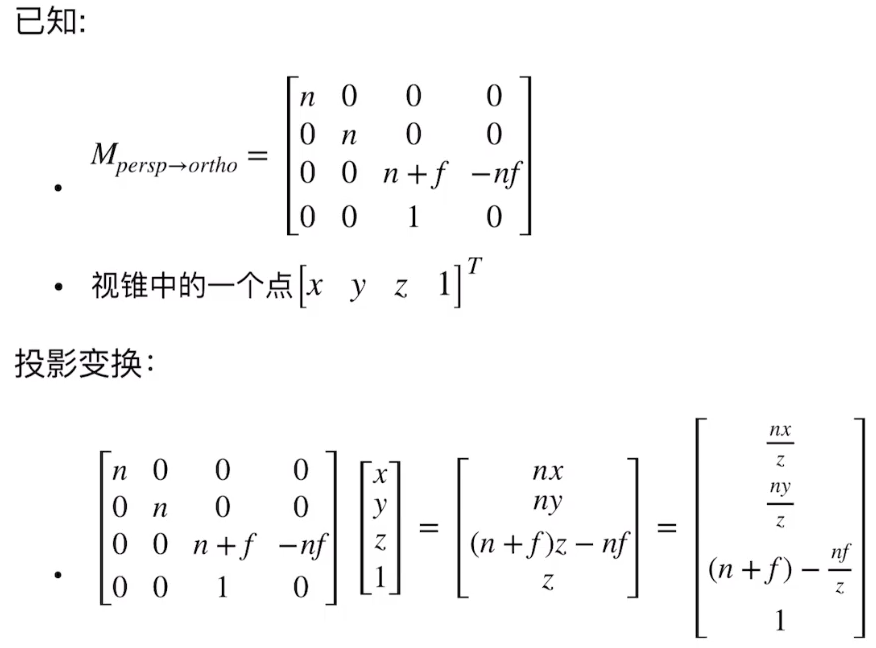
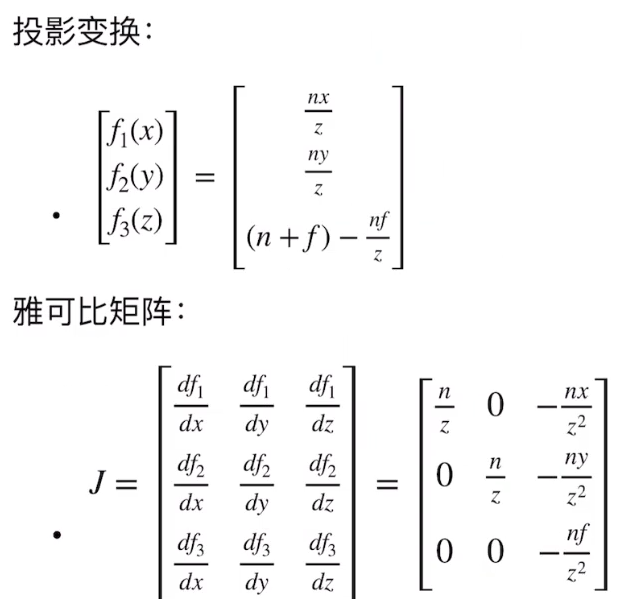
(需要注意的是,这里的n在代码里面每一行,比如对fx求导那一行代表的是x轴的焦距,在fy求导那一行是y轴的焦距)
GS视口变换
-
高斯核中心被拉伸到2D平面
μ = [ μ 1 , μ 2 , μ 3 ] T \mu = [\mu_1,\mu_2,\mu_3]^T μ=[μ1,μ2,μ3]T 平移+缩放 -
协方差在还是在原来的地方,协方差只用来做足迹渲染(离散的计算)(距离均值 μ \mu μ越近,值越大) G ( x ^ ) = exp ( − 1 2 ( x − μ ) T V k − 1 ( x − μ ) ) G(\hat{x})=\exp\left(-\frac{1}{2}(x-\mu)^TV_k^{-1}(x-\mu)\right) G(x^)=exp(−21(x−μ)TVk−1(x−μ))
| 高斯核: | 协方差: |
|---|---|
 |  |
光栅化
过程与上述2.2.4一致
小结
| 3D GS中心变换流程 | 3D GS协方差矩阵的变换 |
|---|---|
| 1. 观测变换 2. 投影变换 3. 视口变换 4. 光栅化 | 1. 观测变换(变换到相机坐标系) 2. GS投影变换,返回**二维协方差矩阵(包含 σ x 、 σ y 、 σ x y \sigma_x、\sigma_y、\sigma_{xy} σx、σy、σxy)**,由于是像素平面,Z轴被扔掉了(这里可以控制(0,0)(1,1)值进行滤波) |
球谐函数
球谐函数是一组定义在球面上的特殊函数,通常用来表示球面上的函数。球谐函数用于近似光照和颜色分布,球谐函数定义在球面上,输入视角(θ,ϕ),它的输出是RGB颜色值。(球,在不同方向上反射不同的光的颜色)
- 任意一个球面坐标可以由多个球谐函数来近似
- f ( t ) ≈ ∑ l ∑ m = − l l c l m y l m ( θ , ϕ ) f(t)\approx\sum_{l}\sum_{m=-l}^{l}c_{l}^{m}y_{l}^{m}(\theta,\phi) f(t)≈∑l∑m=−llclmylm(θ,ϕ)
- 其中, c l m c_{l}^{m} clm各项系数, y l m y_{l}^{m} ylm是基函数
- 这个球谐函数这个球是颜色球,跟GS椭球无关
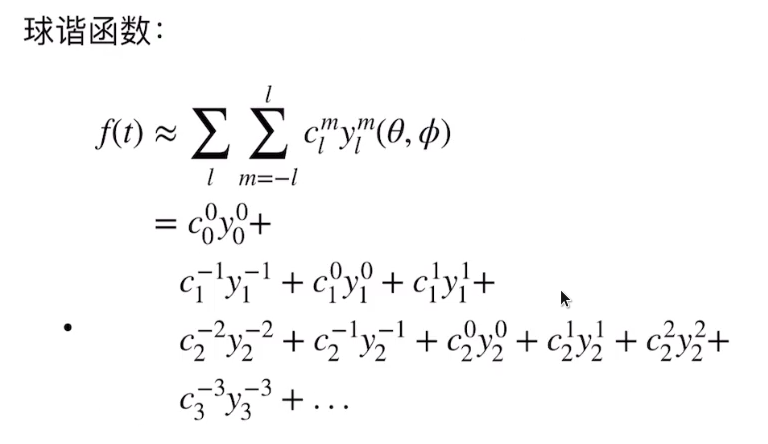
其中:

这里,2阶的球谐函数加起来的颜色形象表示。(球谐函数系数跟阶数相关,1+3+5+7····=n,[n,3]的系数维度越高,表达色彩越复杂)
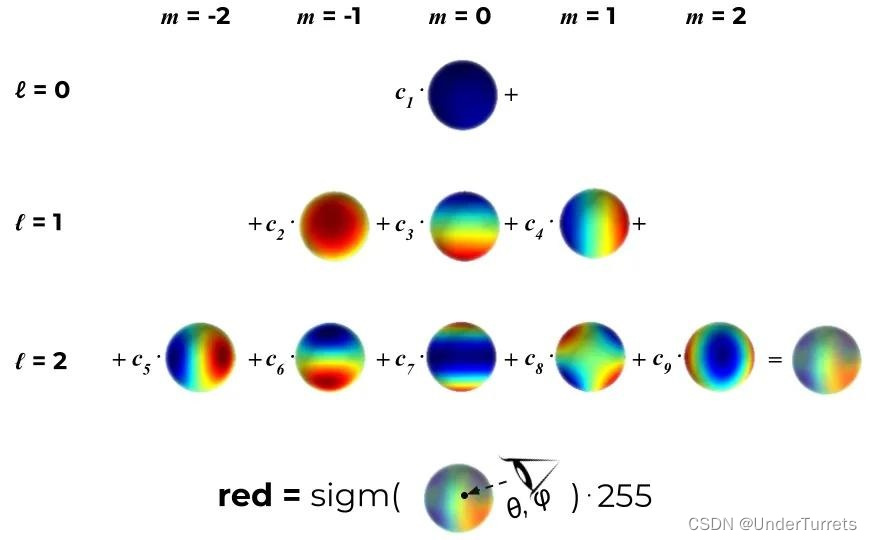
C就是三维系数,Y包含了(xyz)为相机指向高斯椭球的中心来表达方向,不同方向颜色不一样。
球谐函数原理:把环境光球,跟最小外接矩做映射,再把矩形展开。
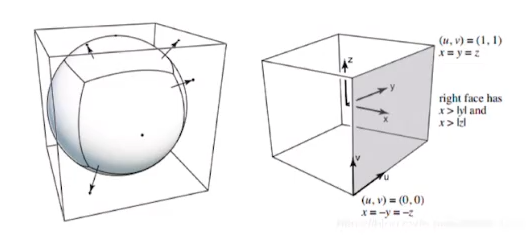


足迹合成
- 把每个高斯生成的足迹(每张图)做alpha-blending
- 实际上,高斯的足迹合成迭代的还是每个像素,对每个像素进行着色
像素颜色合成过程(和Nerf一样):

对像素射线上的粒子连续积分,如果遇到密度较大的后面就不再考虑。方法上由于计算机不能连续积分,一般离散化处理,光线被划分为等间距区间,然后固定区间内密度和颜色固定,累加。

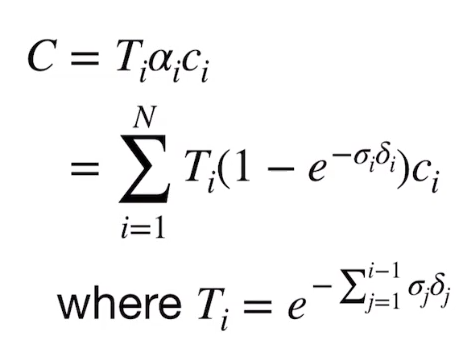
与Nerf不一样的是:
- splatting没有寻找粒子的过程
- 需要对高斯球按照深度z排序(在通过变换到原点的正方体中后,按照深度从近到远来依次往平面“砸”,不同的顺序对图像影响不同)
高性能渲染
问题:3DGS与Nerf像素渲染一样的方式,为什么3DGS要快很多?
3DGS采用GPU部分(并行):
- 高斯椭球也是由初始colmap生成的点云,数量不会小很多。
- splatting部分使用cuda部分编写
- 一个线程负责一个像素
分区处理:
- 整个图片被划分为 16 × 16 16\times16 16×16块
- 对每个高斯划分区块
- 这样GPU的每个block负责一个区
- Block可以共享内存
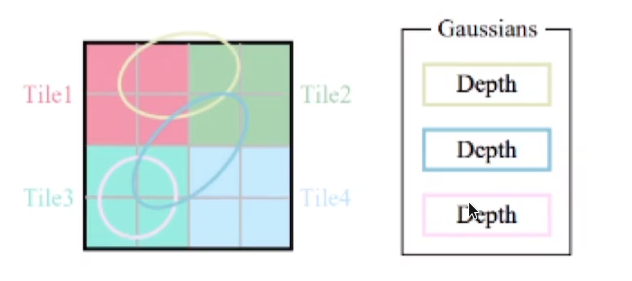
机器学习与参数评估
参数:
- 假设初始点云有10000个点
- 每个点膨胀成3d高斯椭球
- 每个椭球包含的参数包括:
- 中心点位置: ( x , y , z ) (x, y, z) (x,y,z)
- 协方差矩阵:R,S
- 球谐函数系数: 16 × 3 16\times3 16×3
- 透明度: a a a
 步骤:
步骤:
1、使用SfM估计的点云(colmap),利用knn初始化膨胀为3D GS
2、使用所有的高斯点,使用源图像的位姿,渲染出图像
3、根据源图像和渲染图像,计算损失,并反向传播进行优化。优化的对象有:
协方差矩阵,Covariance matrix
不透明度,Opacity α
球谐函数,Spherical harmonics
4、对高斯点的数量进行控制,即进行克隆、分裂或者删除
3DGS的初始化
~/gaussian-splatting/submodules
- diff-gaussian-rateriztion //渲染部分
- simple-knn //将临近的GS点融合
Knn作用:
- 是一个球(各向同性)
- 使用knn,找到3近领
- 半径是与3近邻的距离的平均
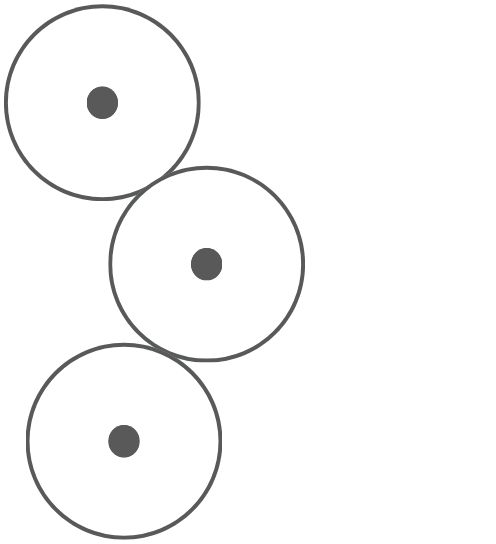
问题:
强依赖SfM生成的初始点云
方法:自适应高斯的控制器(Adaptive Control of Gaussians)
- 太大的拆分
- 太小的合并
- 存在感太低的剔除
删除:在优化预热之后,每一百次迭代,就会删除几乎透明的高斯点,即不透明度 a a a小于阈值 ϵ a \epsilon_a ϵa的高斯。 ϵ a \epsilon_a ϵa是个超参数,经验上设置为0.0002。
克隆和分裂:
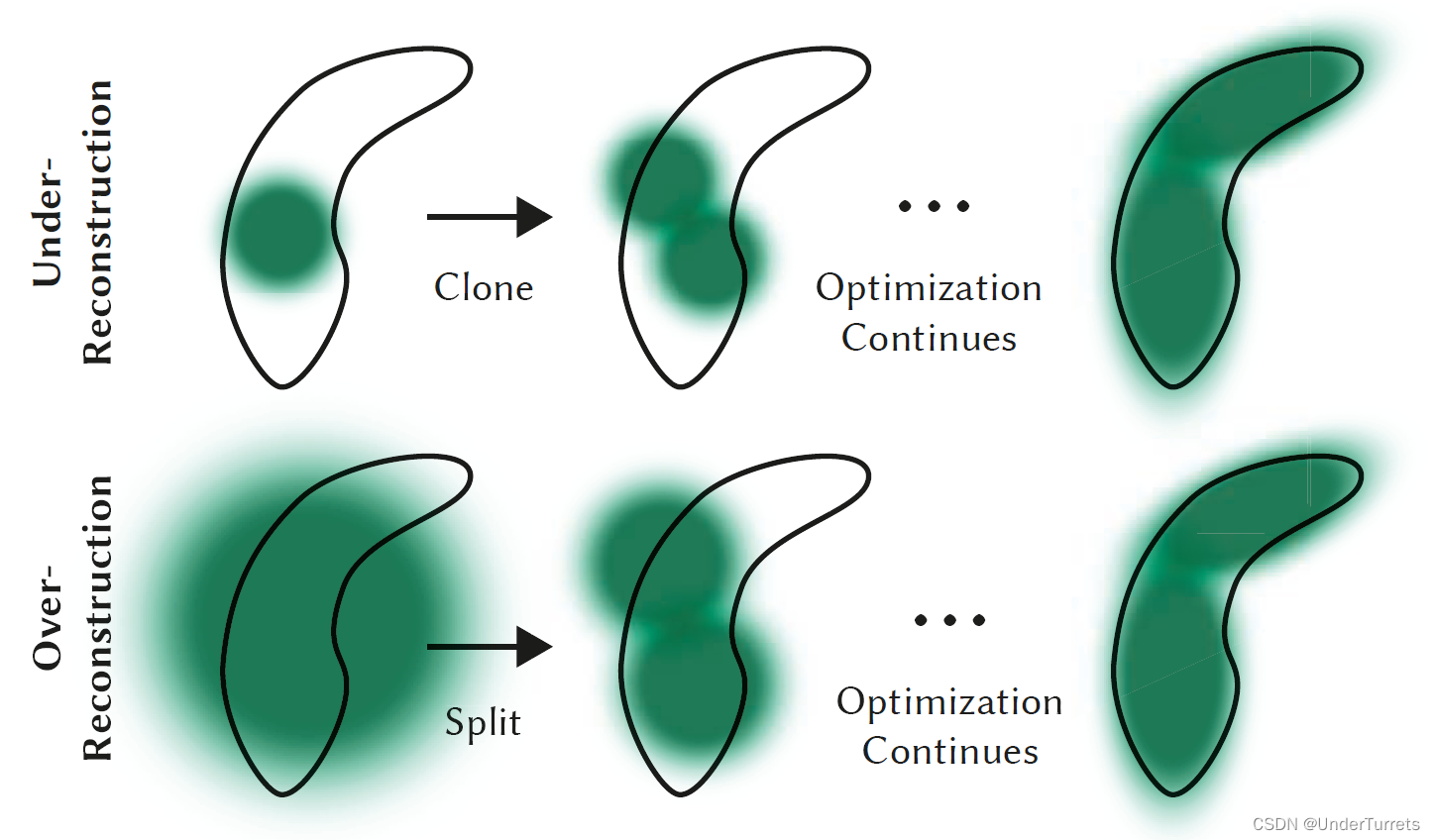
- 对于重建不足的高斯点,克隆一个相同大小的副本,并且沿着位置梯度方向移动。
- 对于过度重建的高斯点,对它进行分裂,分裂时还需要确定比例,经验上以超参数 ϕ = 1.6作为这个比例。
3D GS splatting过程的效果
相机坐标 (0,0,5)
空间点坐标 (2, 0, -2), (0, 2, -2), (-2, 0, -2), (0, 0, 0)
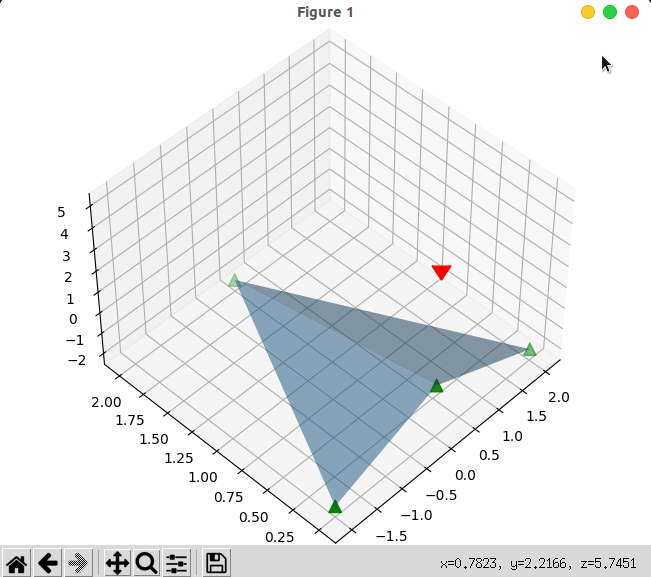
光栅化:
3DGS:
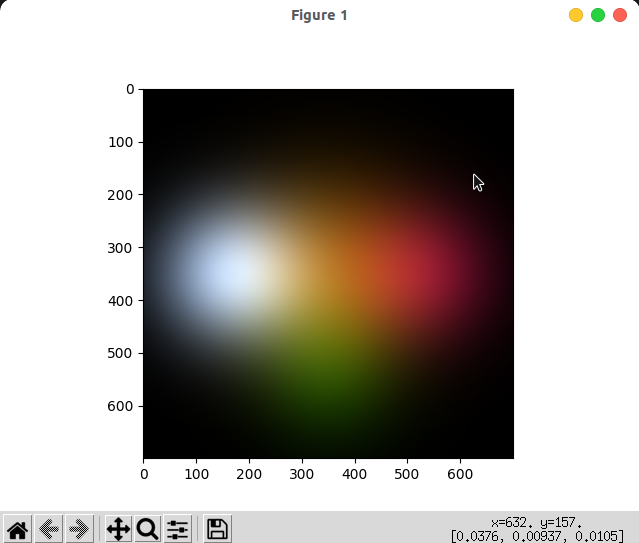






















 3357
3357

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








