Python量化交易(六)：量化调仓策略

---

引言

大家好，我是GISer Liu😁，一名热爱AI技术的GIS开发者。本系列文章是我跟随DataWhale 2024年10月学习赛的Python量化交易学习总结文档。
在现代金融市场中，投资组合的优化与风险管理已成为投资者追求稳健收益的关键。本文将系统梳理投资组合的收益率衡量方法、风险的定义与衡量方式，重点解析常见的最优化方法，并介绍如何使用Python进行投资组合的最佳仓位控制。通过本文的学习，您将掌握投资组合管理的核心概念和实用工具，提升在复杂市场环境中的决策能力。

---

一、 投资组合的收益率衡量

1. 投资组合收益率的计算方法

投资组合的收益率是衡量投资组合表现的重要指标，它可以帮助投资者评估投资组合的回报水平，并与市场指数或其他投资组合进行比较。

• 投资组合收益率的计算：假设投资组合中有 n 个资产，每个资产的收益率为 r1, r2, ..., rn，每个资产的权重为 w1, w2, ..., wn，则投资组合的收益率为：

$\text{投资组合的收益率}=w_1\times r_1+w_2\times r_2+...+w_n\times r_n$

其中，权重 wi 表示资产 i 在投资组合中的占比，满足 w1 + w2 + ... + wn = 1。

2. 投资组合的绝对收益率和相对收益率

投资组合的收益率不仅取决于投资组合本身的表现，还取决于市场的整体表现。因此，在比较投资组合的收益率时，需要将其与市场平均收益进行比较，以便更好地评估投资组合的表现。

• 绝对收益率：投资组合的实际收益与初始投资金额之间的比率。

$\text{绝对收益率}=\frac{\text{投资组合的实际收益}-\text{初始投资金额}}{\text{初始投资金额}}\times 100$

例如，初始投资金额为 10000 元，最终实现的收益为 12000 元，则绝对收益率为 20%。

• 相对收益率：投资组合的实际收益与市场平均收益之间的比率。

$\text{相对收益率}=\frac{\text{投资组合的实际收益}-\text{市场平均收益}}{\text{市场平均收益}}\times 100$

例如，投资组合实现的收益为 12000 元，而市场平均收益为 10000 元，则相对收益率为 20%。

类别	作用	公式
投资组合收益率	衡量投资组合表现的重要指标，帮助投资者评估回报水平并与市场指数比较	$\text{投资组合的收益率}=w_1\times r_1+w_2\times r_2+...+w_n\times r_n$
绝对收益率	投资组合的实际收益与初始投资金额之间的比率	$\text{绝对收益率}=\frac{\text{投资组合的实际收益}-\text{初始投资金额}}{\text{初始投资金额}}\times 100\%$
相对收益率	投资组合的实际收益与市场平均收益之间的比率	$\text{相对收益率}=\frac{\text{投资组合的实际收益}-\text{市场平均收益}}{\text{市场平均收益}}\times 100\%$

• 投资组合收益率：用于评估整个投资组合的综合表现，适合与市场指数或其他投资组合进行比较。
• 绝对收益率：用于衡量投资组合的实际回报，适合评估投资的盈利能力和风险。
• 相对收益率：用于评估投资组合相对于市场的表现，适合评估投资策略的有效性和市场风险调整后的收益。

二、风险的定义

1. 风险的定义

风险是指在未来可能发生的不确定性事件所带来的潜在损失。在投资领域中，风险通常指投资所面临的不确定性和潜在的损失。

• 投资组合的风险：投资组合在未来可能出现的损失或波动的程度。投资组合的风险通常由其波动性、损失概率和损失幅度等因素来衡量。

2. 衡量投资组合的风险

投资组合的风险可以通过多种方式进行衡量，以下是一些常见的方法:

① 方差和标准差

方差和标准差是衡量投资组合波动性的常用指标。方差是每个资产收益率与平均收益率之差的平方的平均值，标准差是方差的平方根。

$\sigma 2=\frac{1}{n}{\sum }_{i=1}n(x_i-\mu {)}^2$

$\sigma =\sqrt{\frac{1}{n}{\sum }_{i=1}n(x_i-\mu )2}$

其中，xi 表示第 i 个数据点，μ 表示所有数据点的平均值，n 表示数据点的数量。

② Beta系数

Beta系数是衡量投资组合相对于市场整体波动的指标，用投资组合与市场组合的协方差与市场组合的方差的比值计算。

${\beta }_i=\frac{\text{Cov}(r_i,r_m)}{\text{Var}(r_m)}$

Beta系数为1表示投资组合的波动与市场整体波动相同，小于1表示波动小于市场整体波动，大于1表示波动大于市场整体波动。

③ Value at Risk（VaR）

VaR是衡量投资组合在一定置信水平下的最大可能损失的指标。

${\text{VaR}}_{\alpha }(L)=\inf y\in \mathbb{R}\mid F_L(y)\ge \alpha$

例如，一个10%的VaR表示在90%的时间内，投资组合的损失不会超过VaR的值。

④ Conditional Value at Risk（CVaR）

CVaR是VaR的扩展，它衡量的是在VaR损失超过一定阈值时的平均损失。

$\text{CVaR}1-\alpha =-\int 0^{1-\alpha }{\text{VaR}}_{\alpha }(L)dr$

CVaR模型在一定程度上克服了VaR模型的缺点，不仅考虑了超过VaR值的频率，而且考虑了超过VaR值损失的条件期望，有效的改善了VaR模型在处理损失分布的后尾现象时存在的问题。

这里作者将其整理为表格方便记忆:

类别	作用	公式
方差和标准差	衡量投资组合的波动性，反映投资组合收益率的离散程度; 适用于评估投资组合的整体风险，不考虑市场整体波动。	${\sigma }^2=\frac{1}{n}{\sum }_{i=1}^n(x_i-\mu {)}^2$$\sigma =\sqrt{\frac{1}{n}{\sum }_{i=1}^n(x_i-\mu {)}^2}$
Beta系数	衡量投资组合相对于市场整体波动的敏感性; 适用于评估投资组合相对于市场的风险，反映投资组合与市场波动的相关性。	${\beta }_i=\frac{\text{Cov}(r_i,r_m)}{\text{Var}(r_m)}$
Value at Risk	衡量在一定置信水平下投资组合的最大可能损失: 适用于评估投资组合在特定置信水平下的风险，但可能忽略极端损失的情况。	${\text{VaR}}_{\alpha }(L)=\inf y\in \mathbb{R}\mid F_L(y)\ge \alpha$
Conditional Value at Risk	衡量在VaR损失超过一定阈值时的平均损失，克服VaR模型的缺点: 适用于评估投资组合在极端情况下的风险，考虑了超过VaR值的频率和条件期望	${\text{CVaR}}_{1-\alpha }=-{\int }_0^{1-\alpha }{\text{VaR}}_{\alpha }(L)dr$

3. 案例说明

投资组合的风险会在多种情况下发生，以下是一些常见的情况及其举例说明：

① 市场波动性增加

情况：市场整体波动性增加，导致投资组合的收益率波动加大。
举例：

• 方差和标准差：假设某投资组合在正常市场条件下的标准差为5%，但在市场波动性增加时，标准差可能上升到10%。
• Beta系数：某股票的Beta系数为1.5，在市场波动性增加时，该股票的波动性可能比市场整体波动性高出50%。

② 市场下跌

情况：市场整体下跌，导致投资组合的收益率下降。
举例：

• Value at Risk (VaR)：假设某投资组合的VaR为5%，在市场下跌时，投资组合的损失可能超过5%。
• Conditional Value at Risk (CVaR)：在市场下跌时，CVaR可能显示投资组合在超过VaR值时的平均损失为7%。

③ 极端事件

情况：发生极端事件（如金融危机、自然灾害等），导致市场剧烈波动。
举例：

• 方差和标准差：在金融危机期间，投资组合的标准差可能急剧上升，反映出收益率的极端波动。
• Beta系数：在极端事件期间，某些高Beta股票的波动性可能显著增加，导致投资组合的整体风险上升。

④ 资产相关性变化

情况：投资组合中资产之间的相关性发生变化，导致投资组合的风险增加。
举例：

• 方差和标准差：假设某投资组合由两只股票组成，正常情况下两只股票的相关性较低，但在市场波动性增加时，两只股票的相关性可能上升，导致投资组合的标准差增加。
• Beta系数：在市场波动性增加时，某些资产的Beta系数可能上升，导致投资组合相对于市场的波动性增加。

⑤ 流动性风险

情况：市场流动性下降，导致资产难以以合理价格买卖。
举例：

• Value at Risk (VaR)：在市场流动性下降时，投资组合的VaR可能上升，因为资产难以以合理价格卖出，导致潜在损失增加。
• Conditional Value at Risk (CVaR)：在市场流动性下降时，CVaR可能显示投资组合在超过VaR值时的平均损失增加，反映出流动性风险的影响。

• 方差和标准差：适用于评估市场波动性增加时的整体风险。
• Beta系数：适用于评估市场整体波动对投资组合的影响。
• Value at Risk (VaR)：适用于评估市场下跌或极端事件时的潜在损失。
• Conditional Value at Risk (CVaR)：适用于评估极端事件或流动性风险时的平均损失。

三、最优化方法计算投资组合的最佳仓位

在复杂的市场环境中，投资者追求在给定风险水平下最大化收益，或在给定收益水平下最小化风险。传统的投资策略（如等权重、市值加权）虽然简单易行，但往往无法在复杂的市场环境中实现最优的收益风险平衡。因此，投资者需要借助最优化方法，通过数学模型和算法，灵活应对不同的投资目标和约束条件，提高投资决策的科学性和精确性。

• 思路:

最优化方法通过多种数学模型和算法，帮助投资者在复杂的市场环境中找到最佳的投资组合配置。这些方法包括等权重、市值加权、最小方差组合、最大分散度、风险平价和均值方差优化等。每种方法都有其独特的目标和数学表达，旨在实现收益最大化与风险最小化的平衡。

• 案例

假设投资者希望在不超过10%的风险水平下最大化收益。通过均值方差优化，投资者可以找到在10%风险水平下的最优组合，而不是简单地平均分配资金。在市场波动性增加时，最大分散度优化可以帮助投资者调整组合，降低高波动性资产的权重，增加低波动性资产的权重，从而降低整体风险。

下面我们详细介绍一下具体的方法：

1. 等权重

在没有任何信息或者偏好时，等权重是最简单的办法，即赋予组合中每个证券相同的权重，意味着我们视每个证券具有同等的重要性。

• 等权重组合：假设组合中有 N 个证券，每个证券的权重为：

${\omega }_i=\frac{1}{N}$

等权重组合的业绩表现往往是非常抢眼的，因此在研究中常被用来作为比较基准。

2. 市值加权

对于股票组合而言，在没有任何信息或者偏好时，还有另外一种使用非常普遍的组合方法，即市值加权。

• 市值加权组合：根据定义，对于选出的股票，按照其市值加权，即：

${\omega }_i=\frac{{\text{Cap}}_i}{{\sum }_i{\text{Cap}}_i}$

其中，$Ca{p}_i$为股票 i 的市值。市值加权不需要频繁调仓，往往流动性也最强。

3. 最小方差组合

对于风险厌恶的投资者，自然是希望投资者的风险是最小的。由于总体的风险是未知的，在组合优化中，我们常常用历史收益率的方差最为代理变量，追求组合整体的方差最小。

• 最小方差组合：数学表达为：

$\text{Min}{\sigma }_p={\omega }^{\prime }\Sigma \omega \Rightarrow \omega \propto {\Sigma }^{-1}1$

4. 最大分散度

从组合的方差-协方差矩阵我们可知，组合的整体风险一部分来源于各个证券自身的方差，另一部分来源于证券之间的协方差。因此，如果我们想降低组合风险，就应该尽量分散投资。

• 最大分散度优化：数学表达为：

$\text{Max},D(w)=\frac{{\omega }^{\prime }\sigma }{{\omega }^{\prime }\Sigma \omega }\Rightarrow \omega \propto {\Sigma }^{-1}\sigma$

目标函数被称为分散比率，分母为组合波动率，分子为成分的波动率加权平均。

5. 风险平价

风险平价（Risk Parity）从风险的角度进行均衡配置，以追求所有证券对组合的风险贡献相同。

• 风险平价组合：数学表达为：

$\text{Min},{\sum }_{i=1}N{\sum }_{j=1}N(R{C}_i-R{C}_j{)}^2\Rightarrow {\omega }_i\propto \frac{1}{{\beta }_i}$

在 Risk Parity 投资组合中，证券的权重和它相对于组合的 β 成反比；β 越高，其权重越低，从而有效的分散了风险，每个资产对组合的边际风险贡献相同。

6. 均值方差优化

一个优秀的投资策略，往往是在给定风险水平下实现组合收益最大化，或者在给定收益水平实现组合风险最小化。

• 均值方差优化：目标函数为：

$\text{Max}{\omega }^T\mu -\frac{\lambda }{2}{\omega }^{\prime }\Sigma \omega$

理论上来讲，组合成分间存在无数个混搭方式，每种方式得到一个收益风险对，将所有结果集合在一起，就形成了可行域，如图所示。可行域中并不是所有点都是“好结果”，只有处于可行域上侧边缘的点才是最优值，即MVO的解，如图中A到D之间连线，这条线称为有效前沿。

• 
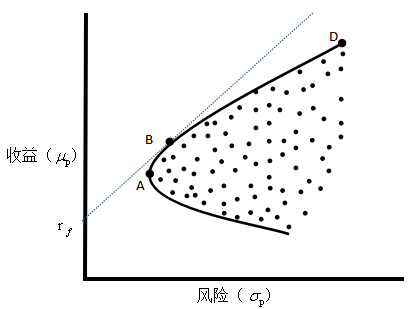
• 任何异于有效前沿曲线的点，均能找到相同风险（收益）下收益（风险）更高（低）的组合；上图的A点为最小方差组合，B点为可行域中夏普比率最大的点，因此也被称为最大夏普组合；

7. 常见约束

在实际投资中，往往除了最现实的资金限制外，还会有各种各样的限制。

• 单资产权重的范围限制：

${\omega }_{lb}\le \omega \le {\omega }_{ub}$

• 做空限制：

${\omega }^{T}1=1,\omega \ge 0$

• 行业中性化：

$(\omega -{\omega }_{\text{benchmark}}{)}^T{I}_{\text{industry}\in D}=0$

• 风险敞口限制：

$|(\omega -{\omega }_{\text{benchmark}}{)}^{T}f|\le f_{ub}\in [0,1]$

为了方便记忆，作者这里将其整理为表格：

方法类别	作用	思路
等权重	简单分配资金	每个证券赋予相同的权重，适用于无偏好或信息的情况。
市值加权	基于市场规模分配资金	根据股票市值分配权重，流动性强，不需要频繁调仓。
最小方差组合	最小化组合风险	通过最小化组合的历史收益率方差来降低风险。
最大分散度	降低组合风险	通过最大化分散比率，降低高波动性资产权重，增加低波动性资产权重。
风险平价	均衡风险贡献	使每个证券对组合的风险贡献相同，权重与β成反比。
均值方差优化	最大化收益与风险平衡	在给定风险水平下最大化收益，或在给定收益水平下最小化风险。
常见约束	实际投资限制	包括单资产权重范围、做空限制、行业中性化、风险敞口限制等。

四、Python实现最佳仓位控制

1.安装必要的库

pip install akshare scipy

2.导入必要的库

import akshare as ak
import datetime
import warnings
import pandas as pd
import numpy as np
from scipy.optimize import minimize
import matplotlib.pyplot as plt
import matplotlib.font_manager as fm

3.配置绘图中文字符

# 设置中文字体
font_path = 'C:/Windows/Fonts/simhei.ttf'  # 例如，使用黑体
prop = fm.FontProperties(fname=font_path)
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号

4.定义权重配置函数

def get_weights(df: pd.DataFrame, target='sharp', canshort=False) -> pd.Series:
    '''
    :param df: 资产日度涨跌幅矩阵
    :param target: 优化目标 sharp→最大夏普比组合 rp→风险平价组合  var→最小风险组合
    :param canshort: 是否可以做空
    :return: 组合比率
    '''
    MeanReturn = df.mean().values  # 期望收益
    Cov = df.cov()  # 协方差
   
    # 定义优化函数、初始值、约束条件
    # 负夏普比
    def neg_sharp(w):
        R = w @ MeanReturn
        Var = w @ Cov @ w.T
        sharp = R / Var ** 0.5
        return -sharp * np.sqrt(240)

    # 风险
    def variance(w):
        Var = w @ Cov @ w.T
        return Var * 10000

    def RiskParity(w):
        weights = np.array(w)  # weights为一维数组
        sigma = np.sqrt(np.dot(weights, np.dot(Cov, weights)))  # 获取组合标准差
        MRC = np.dot(Cov, weights) / sigma  # MRC = Cov@weights/sigma
        TRC = weights * MRC
        delta_TRC = [sum((i - TRC) ** 2) for i in TRC]
        return sum(delta_TRC)

    # 设置初始值
    w0 = np.ones(df.shape[1]) / df.shape[1]
    # 约束条件 w之和为1
    cons = [{'type': 'eq', 'fun': lambda w: np.sum(w) - 1}]
    bnds = tuple((0, 1) for w in w0)  # 做多的约束条件，如果可以做空，则不传入该条件

    if target == 'sharp':
        fc = neg_sharp
    elif target == 'rp':
        fc = RiskParity
    elif target == 'var':
        fc = variance

    if canshort:
        res = minimize(fc, w0, method='SLSQP', constraints=cons, options={'maxiter': 100})
    else:
        res = minimize(fc, w0, method='SLSQP', constraints=cons, options={'maxiter': 100}, bounds=bnds)

    weight = pd.Series(res.x, index=df.columns)
    return weight

5.下载股票的复权收盘价，计算日收益率

def get_ret(code, start_date, end_date):
    data = ak.stock_zh_a_hist(symbol=code, period="daily", start_date=start_date, end_date=end_date, adjust="hfq")
    data.index = pd.to_datetime(data['日期'], format='%Y-%m-%d')  # 设置日期索引
    close = data['收盘']  # 日收盘价
    close.name = code
    ret = close.pct_change()  # 日收益率
    return ret

end_date = datetime.datetime.now().strftime('%Y%m%d')
index_stock_cons_weight_csindex_df = ak.index_stock_cons_weight_csindex(symbol="000016")
stock_codes = index_stock_cons_weight_csindex_df['成分券代码'].to_list()
start_date = (index_stock_cons_weight_csindex_df['日期'].iat[0] - pd.Timedelta(days=365 * 1)).strftime('%Y%m%d')

ret_list = []
for code in stock_codes:
    ret = get_ret(code, start_date=start_date, end_date=end_date)
    ret_list.append(ret)
df_ret = pd.concat(ret_list, axis=1).dropna()

6.在时间轴上滚动计算最优化模型的权重

records = []
for trade_date in df_ret.loc[index_stock_cons_weight_csindex_df['日期'].iat[0]:].index.to_list():
    df_train = df_ret.loc[:trade_date].iloc[-1 - 240:-1]
    df_test = df_ret.loc[trade_date]
    StockSharpDf = get_weights(df_train, target='sharp')  # 最大夏普组合
    StockRPDf = get_weights(df_train, target='rp')  # 风险平价组合
    StockVarDf = get_weights(df_train, target='var')  # 最小风险组合
    records.append([trade_date,
                    (df_test.mul(StockSharpDf)).sum(),
                    (df_test.mul(StockRPDf)).sum(),
                    (df_test.mul(StockVarDf)).sum(),
                    df_test.mean()])
df_record = pd.DataFrame(records, columns=['日期', '最大夏普组合', '风险平价组合', '最小风险组合', '等权重组合'])
df_record = df_record.set_index('日期')

7.可视化不同权重组合下时间序列的累计组合收益率并输出

# 绘制图表
df_record_cum.plot(figsize=(12, 8), title='组合累计收益率对比')
plt.ylabel('累计收益率')
plt.xlabel('日期')
plt.legend()
plt.show()

# 输出分析结果
print("最大夏普组合累计收益率: ", df_record_cum['最大夏普组合'].iloc[-1])
print("风险平价组合累计收益率: ", df_record_cum['风险平价组合'].iloc[-1])
print("最小风险组合累计收益率: ", df_record_cum['最小风险组合'].iloc[-1])
print("等权重组合累计收益率: ", df_record_cum['等权重组合'].iloc[-1])

完整代码如下：

import akshare as ak
import datetime
import warnings
import pandas as pd
import numpy as np
from scipy.optimize import minimize
import matplotlib.pyplot as plt
import matplotlib.font_manager as fm

warnings.filterwarnings('ignore')

# 设置中文字体
font_path = 'C:/Windows/Fonts/simhei.ttf'  # 例如，使用黑体
prop = fm.FontProperties(fname=font_path)
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号

def get_weights(df: pd.DataFrame, target='sharp', canshort=False) -> pd.Series:
    '''
    :param df: 资产日度涨跌幅矩阵
    :param target: 优化目标 sharp→最大夏普比组合 rp→风险平价组合  var→最小风险组合
    :param canshort: 是否可以做空
    :return: 组合比率
    '''
    MeanReturn = df.mean().values  # 期望收益
    Cov = df.cov()  # 协方差
   
    # 定义优化函数、初始值、约束条件
    # 负夏普比
    def neg_sharp(w):
        R = w @ MeanReturn
        Var = w @ Cov @ w.T
        sharp = R / Var ** 0.5
        return -sharp * np.sqrt(240)

    # 风险
    def variance(w):
        Var = w @ Cov @ w.T
        return Var * 10000

    def RiskParity(w):
        weights = np.array(w)  # weights为一维数组
        sigma = np.sqrt(np.dot(weights, np.dot(Cov, weights)))  # 获取组合标准差
        MRC = np.dot(Cov, weights) / sigma  # MRC = Cov@weights/sigma
        TRC = weights * MRC
        delta_TRC = [sum((i - TRC) ** 2) for i in TRC]
        return sum(delta_TRC)

    # 设置初始值
    w0 = np.ones(df.shape[1]) / df.shape[1]
    # 约束条件 w之和为1
    cons = [{'type': 'eq', 'fun': lambda w: np.sum(w) - 1}]
    bnds = tuple((0, 1) for w in w0)  # 做多的约束条件，如果可以做空，则不传入该条件

    if target == 'sharp':
        fc = neg_sharp
    elif target == 'rp':
        fc = RiskParity
    elif target == 'var':
        fc = variance

    if canshort:
        res = minimize(fc, w0, method='SLSQP', constraints=cons, options={'maxiter': 100})
    else:
        res = minimize(fc, w0, method='SLSQP', constraints=cons, options={'maxiter': 100}, bounds=bnds)

    weight = pd.Series(res.x, index=df.columns)
    return weight


def get_ret(code, start_date, end_date):
    data = ak.stock_zh_a_hist(symbol=code, period="daily", start_date=start_date, end_date=end_date, adjust="hfq")
    data.index = pd.to_datetime(data['日期'], format='%Y-%m-%d')  # 设置日期索引
    close = data['收盘']  # 日收盘价
    close.name = code
    ret = close.pct_change()  # 日收益率
    return ret

end_date = datetime.datetime.now().strftime('%Y%m%d')
index_stock_cons_weight_csindex_df = ak.index_stock_cons_weight_csindex(symbol="000016")
stock_codes = index_stock_cons_weight_csindex_df['成分券代码'].to_list()
start_date = (index_stock_cons_weight_csindex_df['日期'].iat[0] - pd.Timedelta(days=365 * 1)).strftime('%Y%m%d')

ret_list = []
for code in stock_codes:
    ret = get_ret(code, start_date=start_date, end_date=end_date)
    ret_list.append(ret)
df_ret = pd.concat(ret_list, axis=1).dropna()


records = []
for trade_date in df_ret.loc[index_stock_cons_weight_csindex_df['日期'].iat[0]:].index.to_list():
    df_train = df_ret.loc[:trade_date].iloc[-1 - 240:-1]
    df_test = df_ret.loc[trade_date]
    StockSharpDf = get_weights(df_train, target='sharp')  # 最大夏普组合
    StockRPDf = get_weights(df_train, target='rp')  # 风险平价组合
    StockVarDf = get_weights(df_train, target='var')  # 最小风险组合
    records.append([trade_date,
                    (df_test.mul(StockSharpDf)).sum(),
                    (df_test.mul(StockRPDf)).sum(),
                    (df_test.mul(StockVarDf)).sum(),
                    df_test.mean()])
df_record = pd.DataFrame(records, columns=['日期', '最大夏普组合', '风险平价组合', '最小风险组合', '等权重组合'])
df_record = df_record.set_index('日期')

# 计算累计收益率
df_record_cum = (1 + df_record).cumprod() - 1

# 绘制图表
df_record_cum.plot(figsize=(12, 8), title='组合累计收益率对比')
plt.ylabel('累计收益率')
plt.xlabel('日期')
plt.legend()
plt.show()

# 输出分析结果
print("最大夏普组合累计收益率: ", df_record_cum['最大夏普组合'].iloc[-1])
print("风险平价组合累计收益率: ", df_record_cum['风险平价组合'].iloc[-1])
print("最小风险组合累计收益率: ", df_record_cum['最小风险组合'].iloc[-1])
print("等权重组合累计收益率: ", df_record_cum['等权重组合'].iloc[-1])

我们以股票代码000016为例，查看不同组合下最终的累计组合收益率;

运行结果如下：

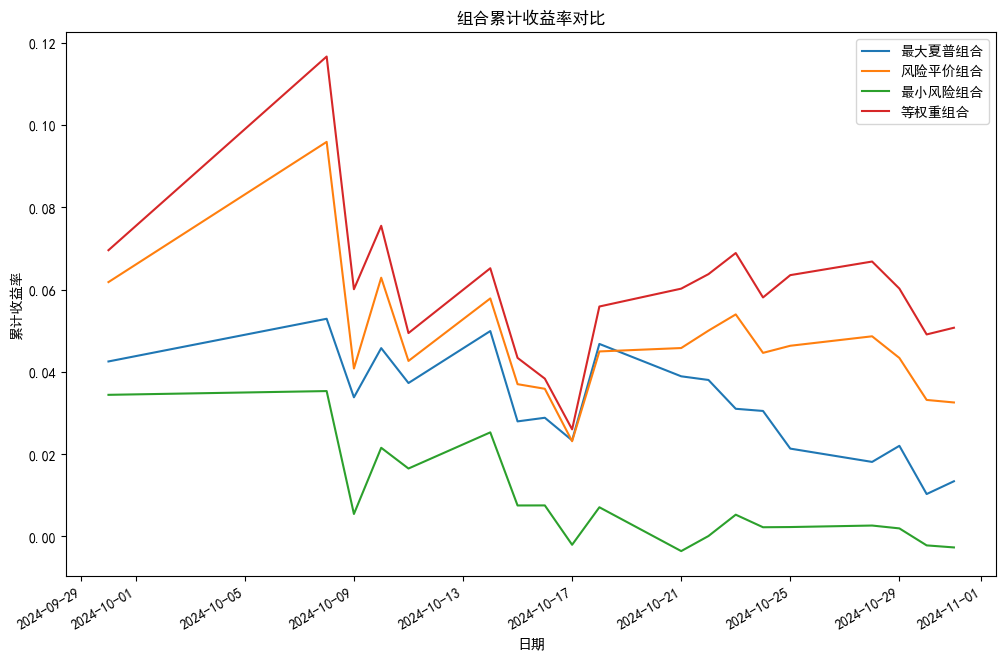
最大夏普组合累计收益率:  0.013409313781817422
风险平价组合累计收益率:  0.03255441274765092
最小风险组合累计收益率:  -0.0026702352488964243
等权重组合累计收益率:  0.050712459752697114

五、投资组合的有效前沿与资本市场线（选修）

1. 效用函数（Utility Function）

效用函数是用来衡量投资者对不同投资组合所获得的满足程度。通过效用函数，我们可以量化投资者在不同风险和收益情况下的满足感，从而进行投资组合的优化。

① 效用函数的公式

效用函数的基本公式如下：

$U=E(R)-\frac{1}{2}\lambda {\sigma }^2$

其中：

• ($E(R)$) 是组合预期收益
• ($\sigma$) 是组合标准差
• ($\lambda$) 是风险厌恶系数

② 效用函数的变形

如果给定效用值 ( U’ )，公式可以变形为：

$E(R)=U^{\prime }+\frac{1}{2}\lambda {\sigma }^2$

这个公式表示在效用不变的情况下，预期收益与风险之间的关系。

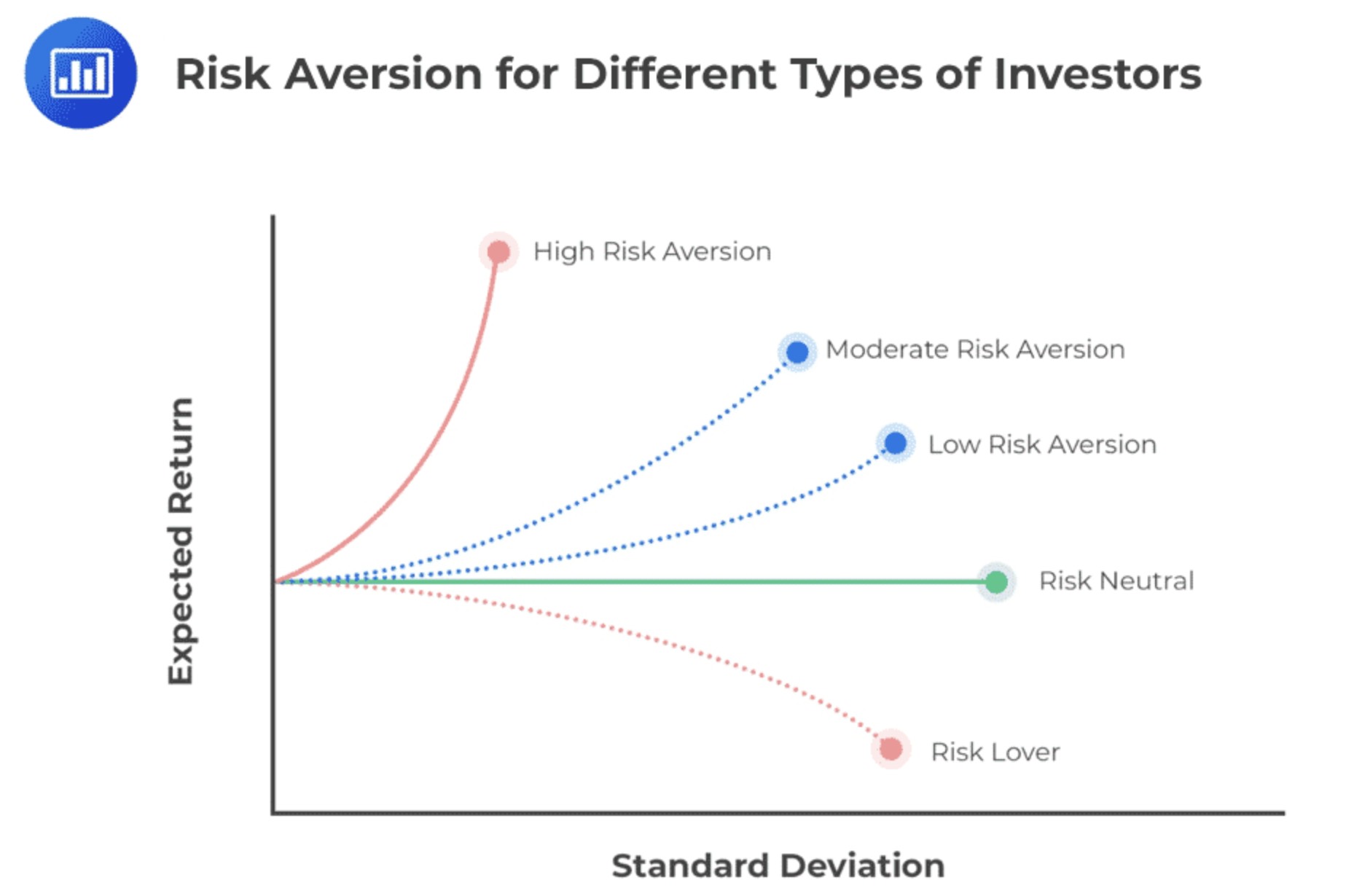
③ 风险厌恶程度的影响

• 风险厌恶（Risk-Averse）：当 ($\lambda$> 0 )，图形为开口向上的曲线。$\lambda$越大，风险厌恶程度越高，曲线开口越窄。
• 风险中性（Risk-Neutral）：当 ($\lambda$= 0 )，投资者对风险不关心。
• 风险喜好（Risk-Seeking）：当 ($\lambda$< 0 )，图形为开口向下的曲线。$\lambda$负的越多，风险喜好程度越高。

2. 无差异曲线（Indifference Curves）

无差异曲线表示在相同的效用下，不同的风险和收益组合。每条曲线上的点都提供相同的效用，投资者可以在这些点之间进行选择。

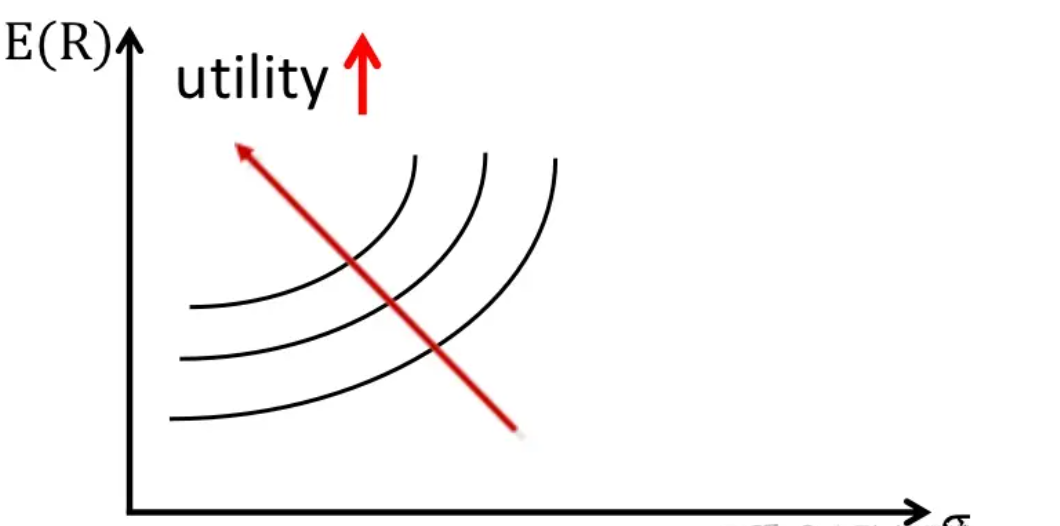
横轴为风险，纵轴为效用；对于风险厌恶者，曲线越往左上侧走，效用越大；

3. 有效前沿（Efficient Frontier）

有效前沿是投资者在不同风险水平下可以获得的最大收益组合的集合。有效前沿上的组合在给定风险下提供最高的预期收益。

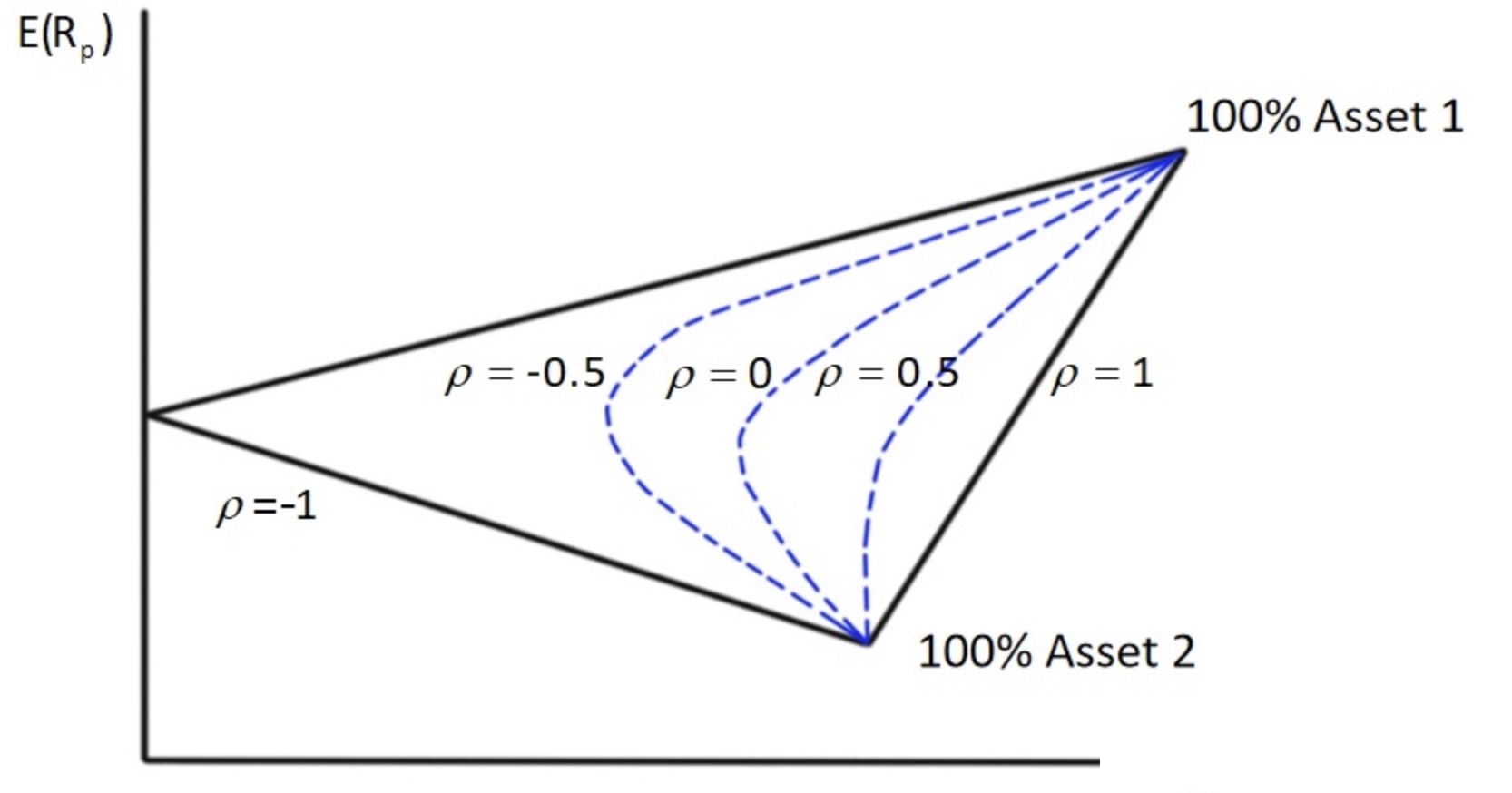
① 两个风险资产的组合

假设有两个风险资产，组合收益和风险分别为：

$R_p=w_1{R}_1+(1-w_1)R_2$
${\sigma }_p=\sqrt{w_{1}2{\sigma }_{1}2+w_{2}2{\sigma }_{2}2+2w_1{w}_2{\rho }_{1,2}{\sigma }_1{\sigma }_2}$

其中：

+${\rho }_{1,2}$是两个资产的相关系数

② 相关系数的影响

• 当 ($\rho$= 1 )，组合风险为线性组合：

${\sigma }_p=w_1{\sigma }_1+w_2{\sigma }_2$

• 当 ($\rho$< 1 )，组合风险小于线性组合：

${\sigma }_p<w_1{\sigma }_1+w_2{\sigma }_2$

• 当 ($\rho$= -1 )，可以通过调整权重使组合风险为零：

${\sigma }_p=|w_1{\sigma }_1-w_2{\sigma }_2|$

4. 资产配置线（Capital Allocation Line）

资产配置线（CAL）表示在考虑无风险资产和风险资产的情况下，投资者可以构建的不同风险和收益组合。

① 资产配置线的公式

$E(R_p)=R_{risk-free}+\frac{E(R_i)-R_{risk-free}}{{\sigma }_i}{\sigma }_p$

其中：

• ($R_{risk-free}$) 是无风险收益率
• ($E(R_i)$) 是风险资产的预期收益率
• (${\sigma }_i$) 是风险资产的标准差

② 无差异曲线与CAL的切点

投资者的最优组合是无差异曲线与CAL的切点。切点处的组合满足投资者的效用最大化。

5. 资本市场线（Capital Market Line）

资本市场线（CML）是在考虑无风险资产和市场组合的情况下，投资者可以构建的最优风险和收益组合。

① CML的公式

$E(R_p)=R_{risk-free}+\frac{E(R_M)-R_{risk-free}}{{\sigma }_M}{\sigma }_p$

其中：

• ($R_M$) 是市场组合的预期收益率
• (${\sigma }_M$) 是市场组合的标准差

② 市场组合与无风险资产的组合

投资者可以通过调整市场组合和无风险资产的权重，构建不同的风险和收益组合。

6. 现代资产组合理论（MPT）

现代资产组合理论（MPT）是由Harry Markowitz在1952年提出的，用于在给定风险水平下最大化收益，或在给定收益水平下最小化风险。

① 风险与收益的衡量

• 风险：使用收益率序列的方差来衡量
• 收益：使用预期收益率来衡量

② 资产组合的优化问题

$\text{min}var(R_p)={\sum }_{i=1}^n{\sum }_{j=1}^{n}cov(R_i,R_j)$
$\text{s.t.}E(R_p)={\sum }_{i=1}^n{w}_{i}E(R_i)\ge \mu ,{\sum }_{i=1}^n{w}_i=1$

7. 资本资产定价模型（CAPM）

资本资产定价模型（CAPM）描述了风险资产的预期收益率与市场组合收益率之间的关系。

① CAPM的公式

$E(R_s)=R_f+{\beta }_s(E(R_M)-R_f)$

其中：

• ( R_s ) 是风险资产的预期收益率
• ( R_f ) 是无风险收益率
• ( R_M ) 是市场组合的预期收益率
• ( \beta_s ) 是风险资产相对于市场的敏感性

② 市场组合的β值

${\beta }_s=\frac{\text{cov}(R_s,R_M)}{\text{var}(R_M)}$

CAPM模型通过引入β值，量化了风险资产的预期收益率与市场组合收益率之间的关系，为投资者提供了一个简单而有效的风险定价工具。

---

相关链接

• 项目地址：AlgoQuant-CookBook
• 相关文档：专栏地址
• 作者主页：GISer Liu-CSDN博客

如果觉得我的文章对您有帮助，三连+关注便是对我创作的最大鼓励！或者一个star🌟也可以😂.

---