文章目录
1.背景
雷达接收机在接收回波信号的同时,不可避免地会遇到噪声,同时还会受到各种干扰,如各种分布物体产生的杂波干扰、敌方施放的噪声调制干扰等。为了选出有用目标,同时抑制各种噪声和干扰,需要滤波器做出频率选择,滤波器是完成这一任务的重要器件。滤波器的频带宽度和频率特性影响滤波效果,直接关系到雷达接收机的灵敏度、波形失真等重要指标。对应于不同的输入信号和噪声干扰,为了使接收机输出端的信号噪声比最大,波形失真最小,要求滤波器有一个最佳的频带宽度和频率特性形状,以实现最佳滤波。
所谓最佳是在某种准则下系统性能达到最佳。在数字通信中,最常采用的最佳准则是输出信噪比最大准则和差错概率最小准则。
最佳线性滤波器的设计通常有两种准则:
- 使滤波器输出的信号波形与发送信号波形之间的均方误差最小——维纳滤波器;
- 使滤波器输出信噪比在某一特定时刻达到最大——匹配滤波器。
2.数字信号接收等效原理图
解调器中抽样判决以前各部分电路可以用一个线性滤波器来等效,如图所示:

这里, n ( t ) n(t) n(t)为高斯白噪声,均值为 0,方差为 σ 2 \sigma^2 σ2,双边功率谱密度为 n 0 2 \frac{n_0}{2} 2n0
抽样判决器输出数据正确与否,与滤波器输出信号波形和发送信号波形之间的相似程度无关,也即与滤波器输出信号波形的失真程度无关;只取决于抽样时刻信号的瞬时功率与噪声平均功率之比,即信噪比
3.匹配滤波器的基本概念
匹配滤波器是在白噪声背景中检测信号的最佳线性滤波器,其输出信噪比在抽样判决时刻
t
=
t
0
t=t_0
t=t0可以达到最大。
4.匹配滤波器的频率响应函数
匹配滤波器的输入信号 r ( t ) = s ( t ) + n ( t ) r(t)=s(t)+n(t) r(t)=s(t)+n(t)
匹配滤波器的输出信号 y ( t ) = s o ( t ) + n o ( t ) y(t)=s_o(t)+n_o(t) y(t)=so(t)+no(t)
其中,根据傅里叶反变换, s o ( t ) = 1 2 π ∫ − ∞ ∞ S o ( ω ) e j ω t d ω = 1 2 π ∫ − ∞ ∞ S ( ω ) H ( ω ) e j ω t d ω s_o(t)=\frac{1}{2\pi}\int_{-∞}^{∞} {\color{Maroon}S_o(\omega)}e^{j\omega t}\,d\omega=\frac{1}{2\pi}\int_{-∞}^{∞} {\color{Maroon}S(\omega)H(\omega)}e^{j\omega t}\,d\omega so(t)=2π1∫−∞∞So(ω)ejωtdω=2π1∫−∞∞S(ω)H(ω)ejωtdω
在
t
=
t
0
t=t_0
t=t0时刻信号的瞬时功率:
∣
s
o
(
t
0
)
∣
2
=
∣
1
2
π
∫
−
∞
∞
S
(
ω
)
H
(
ω
)
e
j
ω
t
0
d
ω
∣
2
\big|s_o(t_0)\big|^2=\Big|\frac{1}{2\pi}\int_{-∞}^{∞} S(\omega)H(\omega)e^{j\omega t_0}\,d\omega\Big|^2
∣∣so(t0)∣∣2=∣∣∣2π1∫−∞∞S(ω)H(ω)ejωt0dω∣∣∣2
噪声的平均功率:
N
o
=
1
2
π
∫
−
∞
∞
P
n
o
(
ω
)
d
ω
=
1
2
π
∫
−
∞
∞
P
n
i
(
ω
)
∣
H
(
ω
)
∣
2
d
ω
=
1
2
π
∫
−
∞
∞
n
0
2
∣
H
(
ω
)
∣
2
d
ω
\begin{aligned} N_o&=\frac{1}{2\pi}\int_{-∞}^{∞} P_{no}(\omega)\,d\omega\\ &=\frac{1}{2\pi}\int_{-∞}^{∞} P_{ni}(\omega)\big|H(\omega)\big|^2\,d\omega\\ &=\frac{1}{2\pi}\int_{-∞}^{∞}\frac{n_0}{2}\big|H(\omega)\big|^2\,d\omega\\ \end{aligned}
No=2π1∫−∞∞Pno(ω)dω=2π1∫−∞∞Pni(ω)∣∣H(ω)∣∣2dω=2π1∫−∞∞2n0∣∣H(ω)∣∣2dω
抽样时刻的输出信噪比:
(
S
N
)
o
=
∣
s
o
(
t
0
)
∣
2
N
o
=
∣
1
2
π
∫
−
∞
∞
H
(
ω
)
S
(
ω
)
e
j
ω
t
0
d
ω
∣
2
n
0
2
1
2
π
∫
−
∞
∞
∣
H
(
ω
)
∣
2
d
ω
(\frac{S}{N})_o=\frac{\big|s_o(t_0)\big|^2}{N_o}=\frac{\Big|\frac{1}{2\pi}\int_{-∞}^{∞} {\color{DarkOrchid}H(\omega)}{\color{Royalblue}S(\omega)e^{j\omega t_0}}\,d\omega\Big|^2}{\frac{n_0}{2}\frac{1}{2\pi}\int_{-∞}^{∞}\big|H(\omega)\big|^2\,d\omega}
(NS)o=No∣∣so(t0)∣∣2=2n02π1∫−∞∞∣∣H(ω)∣∣2dω∣∣∣2π1∫−∞∞H(ω)S(ω)ejωt0dω∣∣∣2
根据
S
c
h
w
a
r
t
z
Schwartz
Schwartz不等式
∣
1
2
π
∫
−
∞
∞
X
(
ω
)
Y
(
ω
)
d
ω
∣
2
≤
1
2
π
∫
−
∞
∞
∣
X
(
ω
)
∣
2
d
ω
1
2
π
∫
−
∞
∞
∣
Y
(
ω
)
∣
2
d
ω
\Big|\frac{1}{2\pi}\int_{-∞}^{∞} X(\omega)Y(\omega)\,d\omega\Big|^2\leq \frac{1}{2\pi}\int_{-∞}^{∞} \big|X(\omega)\big|^2\,d\omega\frac{1}{2\pi}\int_{-∞}^{∞} \big|Y(\omega)\big|^2\,d\omega
∣∣∣2π1∫−∞∞X(ω)Y(ω)dω∣∣∣2≤2π1∫−∞∞∣∣X(ω)∣∣2dω2π1∫−∞∞∣∣Y(ω)∣∣2dω
其中,等号仅当
X
(
ω
)
=
k
Y
∗
(
ω
)
X(\omega)=kY^*(\omega)
X(ω)=kY∗(ω)时成立,这里
k
k
k为不等于0的常数
因此有
(
S
N
)
o
=
∣
1
2
π
∫
−
∞
∞
H
(
ω
)
S
(
ω
)
e
j
ω
t
0
d
ω
∣
2
n
0
2
1
2
π
∫
−
∞
∞
∣
H
(
ω
)
∣
2
d
ω
≤
1
2
π
∫
−
∞
∞
∣
H
(
ω
)
∣
2
d
ω
⋅
1
2
π
∫
−
∞
∞
∣
S
(
ω
)
e
j
ω
t
0
∣
2
d
ω
n
0
2
1
2
π
∫
−
∞
∞
∣
H
(
ω
)
∣
2
d
ω
=
1
2
π
∫
−
∞
∞
∣
S
(
ω
)
∣
2
d
ω
n
0
2
\begin{aligned} (\frac{S}{N})_o&=\frac{\Big|\frac{1}{2\pi}\int_{-∞}^{∞} {\color{DarkOrchid}H(\omega)}{\color{Royalblue}S(\omega)e^{j\omega t_0}}\,d\omega\Big|^2}{\frac{n_0}{2}\frac{1}{2\pi}\int_{-∞}^{∞}\big|H(\omega)\big|^2\,d\omega}\\ &\leq\frac{\frac{1}{2\pi}\int_{-∞}^{∞} \big|H(\omega)\big|^2\,d\omega\cdot\frac{1}{2\pi}\int_{-∞}^{∞} \big|S(\omega)e^{j\omega t_0}\big|^2\,d\omega}{\frac{n_0}{2}\frac{1}{2\pi}\int_{-∞}^{∞}\big|H(\omega)\big|^2\,d\omega}\\ &=\frac{\frac{1}{2\pi}\int_{-∞}^{∞} \big|S(\omega)\big|^2\,d\omega}{\frac{n_0}{2}} \end{aligned}
(NS)o=2n02π1∫−∞∞∣∣H(ω)∣∣2dω∣∣∣2π1∫−∞∞H(ω)S(ω)ejωt0dω∣∣∣2≤2n02π1∫−∞∞∣∣H(ω)∣∣2dω2π1∫−∞∞∣∣H(ω)∣∣2dω⋅2π1∫−∞∞∣∣S(ω)ejωt0∣∣2dω=2n02π1∫−∞∞∣∣S(ω)∣∣2dω
根据帕塞瓦尔定理,信号的能量
E
E
E 可以用时域能量和频域能量表示为
E
=
∫
−
∞
∞
∣
s
(
t
)
2
d
t
=
1
2
π
∫
−
∞
∞
∣
S
(
ω
)
∣
2
d
ω
E=\int_{-∞}^{∞}|s(t)^2\,dt=\frac{1}{2\pi}\int_{-∞}^{∞}|S(\omega)|^2\,d\omega
E=∫−∞∞∣s(t)2dt=2π1∫−∞∞∣S(ω)∣2dω
由此可得
(
S
N
)
o
≤
2
E
n
0
(\frac{S}{N})_o \leq \frac{2E}{n_0}
(NS)o≤n02E
只有当接收机频率响应函数满足:
H
(
ω
)
=
k
S
∗
(
ω
)
e
−
j
w
t
0
{\color{BROWN} H(\omega)=kS^*(\omega)e^{-jwt_0}}
H(ω)=kS∗(ω)e−jwt0
时,上式的等号才成立,此时输入/输出信号噪声比达到最大值,即
(
S
N
)
m
a
x
=
2
E
n
0
{\color{Brown}(\frac{S}{N})_{max} = \frac{2E}{n_0}}
(NS)max=n02E
这表明,当一个线性系统的频率响应函数 H ( ω ) H(\omega) H(ω)为输入信号的复共轭时,其输出的信号噪声比达到最大,这个线性系统称作匹配滤波器。
匹配滤波器的重要特性是:不管输入信号的波形、带宽、持续时间如何,最大输出信号噪声比总是两倍于接收信号能量 ( 2 E ) (2E) (2E) 除以单位带宽的噪声功率 n 0 n_0 n0。这里 n 0 = k T 0 F n n_0=kT_0F_n n0=kT0Fn, k k k为玻尔兹曼常数 ( k = 1.38 × 1 0 − 23 J / K ) (k=1.38×10^{-23} J/K) (k=1.38×10−23J/K), T 0 T_0 T0为室温17℃对应的热力学温度 ( T 0 = 290 ° K ) (T_0=290°K) (T0=290°K), F n F_n Fn为接收机的噪声系数。
5.匹配滤波器的脉冲响应函数
根据傅里叶反变换:
h
(
t
)
=
1
2
π
∫
−
∞
∞
H
(
ω
)
e
j
w
t
d
ω
=
1
2
π
∫
−
∞
∞
k
S
∗
(
ω
)
e
−
j
w
t
0
e
j
w
t
d
ω
=
k
2
π
∫
−
∞
∞
S
∗
(
ω
)
e
−
j
w
(
t
0
−
t
)
d
ω
=
k
2
π
∫
−
∞
∞
[
∫
−
∞
∞
s
(
τ
)
e
−
j
w
τ
d
τ
]
∗
e
−
j
w
(
t
0
−
t
)
d
ω
=
k
∫
−
∞
∞
[
1
2
π
∫
−
∞
∞
e
j
w
(
τ
−
t
0
+
t
)
d
τ
]
s
∗
(
τ
)
d
τ
=
k
∫
−
∞
∞
s
∗
(
τ
)
δ
(
τ
−
t
0
+
t
)
d
τ
=
k
s
∗
(
t
0
−
t
)
\begin{aligned} h(t)&=\frac{1}{2\pi}\int_{-∞}^{∞}H(\omega)e^{jwt}\,d\omega\\ &=\frac{1}{2\pi}\int_{-∞}^{∞}kS^*(\omega)e^{-jwt_0} e^{jwt}\,d\omega\\ &=\frac{k}{2\pi}\int_{-∞}^{∞}S^*(\omega)e^{-jw(t_0-t)}\,d\omega\\ &=\frac{k}{2\pi}\int_{-∞}^{∞}\Big[\int_{-∞}^{∞}s(\tau)e^{-jw\tau}\,d\tau\Big]^*e^{-jw(t_0-t)}\,d\omega\\ &=k\int_{-∞}^{∞}\Big[\frac{1}{2\pi}\int_{-∞}^{∞}e^{jw(\tau-t_0+t)}\,d\tau\Big]s^*(\tau)\,d\tau\\ &=k\int_{-∞}^{∞}s^*(\tau)\delta(\tau-t_0+t)\,d\tau\\ &=ks^*(t_0-t) \end{aligned}
h(t)=2π1∫−∞∞H(ω)ejwtdω=2π1∫−∞∞kS∗(ω)e−jwt0ejwtdω=2πk∫−∞∞S∗(ω)e−jw(t0−t)dω=2πk∫−∞∞[∫−∞∞s(τ)e−jwτdτ]∗e−jw(t0−t)dω=k∫−∞∞[2π1∫−∞∞ejw(τ−t0+t)dτ]s∗(τ)dτ=k∫−∞∞s∗(τ)δ(τ−t0+t)dτ=ks∗(t0−t)
这表明,匹配滤波器的脉冲响应函数 h(t) 是输入信号在时间上的反转后,再向右平移
t
0
t_0
t0时间,即
s
[
−
(
t
−
t
0
)
]
s[-(t-t_0)]
s[−(t−t0)],这等效为频率响应函数 H(ω) 必须有相移
e
−
j
ω
t
0
e^{-j\omega t_0}
e−jωt0。

注:对于一个因果可实现系统
h
(
t
)
=
0
,
t
<
0
h(t)=0,t<0
h(t)=0,t<0
也就是说要求
−
τ
+
t
0
≥
0
-\tau+t_0≥0
−τ+t0≥0,即
t
0
≥
τ
t_0≥ \tau
t0≥τ,而
t
0
t_0
t0是抽样判决时刻,实际上是时延,我们希望时延越小越好,尽早进行判决,因此取
t
0
=
τ
t_0=\tau
t0=τ
6.匹配滤波器的输出信号
匹配滤波器的输出
y
(
t
)
y(t)
y(t)为
y
(
t
)
=
r
(
t
)
∗
h
(
t
)
=
∫
−
∞
∞
r
(
τ
)
h
(
t
−
τ
)
d
τ
y(t)=r(t)*h(t)=\int_{-∞}^{∞}r(\tau)h(t-\tau)d\tau
y(t)=r(t)∗h(t)=∫−∞∞r(τ)h(t−τ)dτ
由于
h
(
t
)
=
k
s
∗
(
t
0
−
t
)
h(t)=ks^*(t_0-t)
h(t)=ks∗(t0−t),因此输出也可表示为
y
(
t
)
=
k
∫
−
∞
∞
r
(
τ
)
s
∗
(
t
0
−
t
+
τ
)
d
τ
=
k
R
r
s
(
t
0
−
t
)
y(t)=k\int_{-∞}^{∞}r(\tau)s^*(t_0-t+\tau)d\tau=kR_{rs}(t_0-t)
y(t)=k∫−∞∞r(τ)s∗(t0−t+τ)dτ=kRrs(t0−t)
其中,
R
r
s
(
t
0
−
t
)
R_{rs}(t_0-t)
Rrs(t0−t)为
r
(
t
)
r(t)
r(t)和
s
∗
(
t
0
−
t
)
s^*(t_0-t)
s∗(t0−t)互相关函数。
可见,匹配滤波的过程可看作接收信号sr与系统冲激响应ht的卷积:
so = conv( sr , ht) = conv( sr , conj(fliplr( si )) );
也可看作雷达接收信号sr与发射信号si的延迟的互相关函数:
so = xcorr( sr , si );
7.匹配滤波器的输出噪声
n
o
(
t
)
=
n
(
t
)
∗
h
(
t
)
=
∫
−
∞
∞
n
(
τ
)
h
(
t
−
τ
)
d
τ
=
k
∫
−
∞
∞
n
(
τ
)
s
(
t
0
−
t
+
τ
)
d
τ
=
k
R
n
s
(
t
0
−
t
)
\begin{aligned} n_o(t)&=n(t)*h(t)\\ &=\int_{-∞}^{∞}n(\tau)h(t-\tau)d\tau\\ &=k\int_{-∞}^{∞}n(\tau)s(t_0-t+\tau)d\tau\\ &=kR_{ns}(t_0-t) \end{aligned}
no(t)=n(t)∗h(t)=∫−∞∞n(τ)h(t−τ)dτ=k∫−∞∞n(τ)s(t0−t+τ)dτ=kRns(t0−t)
其中,
R
n
s
(
t
0
−
t
)
R_{ns}(t_0-t)
Rns(t0−t)为输入噪声与输入信号的互相关函数,由于
n
(
t
)
n(t)
n(t)与
s
(
t
)
s(t)
s(t)不相关,输出的噪声很小。
8.线性调频信号的匹配滤波输出推导
8.1 时域分析
线性调频信号
s
(
t
)
=
r
e
c
t
(
t
T
)
e
j
π
K
t
2
s(t)=rect(\frac{t}{T})e^{j\pi K t^2}
s(t)=rect(Tt)ejπKt2
匹配滤波器的脉冲响应函数
h
(
t
)
=
s
∗
(
−
t
)
=
r
e
c
t
(
t
T
)
e
−
j
π
K
t
2
h(t)=s^*(-t)=rect(\frac{t}{T})e^{-j\pi K t^2}
h(t)=s∗(−t)=rect(Tt)e−jπKt2
匹配滤波器的输出
s
o
u
t
(
t
)
=
s
(
t
)
∗
h
(
t
)
s_{out}(t)=s(t)*h(t)
sout(t)=s(t)∗h(t)
8.2 频域分析
线性调频信号
S
(
f
)
=
1
K
r
e
c
t
(
f
K
T
)
e
−
j
π
f
2
K
e
j
π
4
S(f)=\frac{1}{\sqrt K}rect(\frac{f}{KT})e^{-j\pi \frac{f^2}{K}}e^{j\frac{\pi}{4}}
S(f)=K1rect(KTf)e−jπKf2ej4π
匹配滤波器的频率响应函数
H
(
f
)
=
S
∗
(
f
)
=
1
K
r
e
c
t
(
f
K
T
)
e
j
π
f
2
K
e
−
j
π
4
H(f)=S^*(f)=\frac{1}{\sqrt K}rect(\frac{f}{KT})e^{j\pi \frac{f^2}{K}}e^{-j\frac{\pi}{4}}
H(f)=S∗(f)=K1rect(KTf)ejπKf2e−j4π
匹配滤波器的频率输出
S
o
u
t
(
f
)
=
S
(
f
)
H
(
f
)
=
1
K
r
e
c
t
(
f
K
T
)
S_{out}(f)=S(f)H(f)=\frac{1}{K}rect(\frac{f}{KT})
Sout(f)=S(f)H(f)=K1rect(KTf)
8.3 再变换回时域
s
o
u
t
(
t
)
=
∫
−
∞
∞
S
o
u
t
(
f
)
e
j
2
π
f
t
d
f
=
1
K
∫
−
B
/
2
B
/
2
e
j
2
π
f
t
d
f
=
1
K
e
j
2
π
f
t
j
2
π
t
∣
−
B
/
2
B
/
2
=
1
K
s
i
n
(
π
B
t
)
π
t
=
T
s
i
n
c
(
π
B
t
)
\begin{aligned} s_{out}(t)&=\int_{-∞}^{∞}S_{out}(f)e^{j2\pi ft}df\\ &=\frac{1}{K}\int_{-B/2}^{B/2}e^{j2\pi ft}df\\ &=\frac{1}{K}\frac{e^{j2\pi ft}}{j2\pi t}\Bigg|_{-B/2}^{B/2}\\ &=\frac{1}{K}\frac{sin(\pi Bt)}{\pi t}\\ &=Tsinc(\pi Bt) \end{aligned}
sout(t)=∫−∞∞Sout(f)ej2πftdf=K1∫−B/2B/2ej2πftdf=K1j2πtej2πft∣∣∣∣∣−B/2B/2=K1πtsin(πBt)=Tsinc(πBt)

由此可见,线性调频信号的匹配滤波器输出为sinc函数,其时宽为 τ = 1 B \tau=\frac{1}{B} τ=B1(-4dB点);
根据能量守恒, P 0 P t = T p τ = B T p = D \frac{P_0}{P_t}=\frac{T_p}{\tau}=BT_p=D PtP0=τTp=BTp=D,输出脉冲峰值功率比输入脉冲峰值功率增大了D倍,也就是线性调频信号经过压缩处理后的接收信号幅度峰值是原来发射信号峰值的D的1/2次方。(D为时宽带宽积)
8.4 匹配滤波脉压输出性能分析
-
峰值旁瓣比:
峰值与最大的第一对旁瓣之比。

-
高旁瓣影响:
强目标回波的旁瓣会埋没附近较小目标的主瓣,导致目标丢失。 -
解决方法:
为了提高分辨多目标的能力,必须采用旁瓣抑制或加权技术。
9.线性调频信号脉冲压缩的匹配滤波实现
对于线性调频信号
时域为:
s
(
t
)
=
r
e
c
t
(
t
T
)
e
j
π
K
t
2
s(t)=rect(\frac{t}{T})e^{j\pi K t^2}
s(t)=rect(Tt)ejπKt2
频谱为(驻定相位原理):
S
(
f
)
=
1
K
r
e
c
t
(
f
K
T
)
e
−
j
π
f
2
K
e
j
π
4
S(f)=\frac{1}{\sqrt K}rect(\frac{f}{KT})e^{-j\pi \frac{f^2}{K}}e^{j\frac{\pi}{4}}
S(f)=K1rect(KTf)e−jπKf2ej4π
9.1 时域匹配滤波
根据 h ( t ) = s ∗ ( − t ) h(t)=s^*(-t) h(t)=s∗(−t)可构造时域匹配滤波器为发射信号时间反褶再取共轭,再与发射信号进行线性卷积即可实现脉冲压缩。
s 0 ( t ) = s ( t ) ∗ s ∗ ( − t ) s0(t)=s(t)*s^*(-t) s0(t)=s(t)∗s∗(−t)
ht = conj(fliplr(st));
s = conv(st,ht);
9.2 频域匹配滤波
9.2.1 方法一
- 原理:
将发射信号时间反褶后取共轭得到h(t),补零后计算FFT,再与信号补零后的FFT在频域相乘,最后IFFT。
ht = conj(fliplr(st));
Hf = fft(ht,Nfft);
Sf = fft(st,Nfft);
s = ifft(Hf.*Sf);
- 说明:
- 为什么需要补零?
因为匹配滤波需要计算线性卷积,但 (DFT) FFT 计算的是循环卷积,所以需要对信号进行补零直到长度超过线性卷积的长度。对于点数分别为N1与N2的两信号,它们线性卷积的长度为 N1+N2-1;若循环卷积长度为N,则有如下关系:
① N < N1 + N2 - 1 时,循环卷积是线性卷积长度为 N 的混叠;
② N = N1 + N2 - 1 时,循环卷积 = 线性卷积;
③ N > N1 + N2 - 1 时,循环卷积 = 线性卷积末尾补 N-(N1+N2-1) 个 0 (弃置区)。 - 弃置区位置
由于发射信号时间反褶后再补零,故最终得到IFFT结果后,弃置区位于信号前端。
9.2.2 方法二
- 原理:
将发射脉冲补零后进行FFT,再取共轭(无需反褶),与信号补零后的FFT在频域相乘,最后IFFT。
Hf = conj(fft(st,Nfft));
Sf = fft(st,Nfft);
s = ifft(Hf.*Sf);
-
说明:
-
方法二与方法一的关系?
根据傅里叶变换的性质,时域反褶+共轭 ↔ 频域共轭(方法一);因此,也可先变换到频域再取共轭(方法二)。但由于它们补零时存在是否反褶的差别,故最终结果的弃置区也存在反褶。 -
弃置区位置
由于是直接在发射信号末尾补零,故最终得到IFFT结果后,弃置区位于信号末端。
9.2.3 方法三
直接在频域生成匹配滤波器:
H ( f ) = 1 K r e c t ( f K T ) e j π f 2 K e − j π 4 H(f)=\frac{1}{\sqrt K}rect(\frac{f}{KT})e^{j\pi \frac{f^2}{K}}e^{-j\frac{\pi}{4}} H(f)=K1rect(KTf)ejπKf2e−j4π
然后与信号的FFT在频域相乘,最后IFFT。
Hf = exp(1i*pi*f_h.^2/K);
Sf = fft(st,Nfft);
s = ifft(Hf.*Sf);
10.MATLAB仿真
10.1 线性调频信号的匹配滤波器输出
- 代码:
clear all;
close all;
clc;
%%******************* 线性调频与脉冲压缩 ********************%%
set(0,'defaultfigurecolor','w'); %设置MATLAB的图形窗口背景为白色
%% 线性调频信号参数设置
T = 1e-6; %时宽
B = 200e6; %带宽
Fs = 4*B; %采样率
K = B/T; %调谐频率
N = round(T/(1/Fs) ); %采样点数,四舍五入
%% 产生线性调频信号
t = linspace( -T/2 ,T/2 ,N);
st = ( abs(t) < T/2 ) .* exp( 1j * pi * K * t.^2 );
phase = pi * K * t.^2; %信号相位
f= K * t; %信号频率
%% 频谱
freq = linspace(-Fs/2,Fs/2,N); %频域采样
Sf = fftshift( fft(st) );
%% 时域匹配滤波
% conj()函数用于计算复数的共轭值;
% fliplr()函数将数组从左到右翻转.
ht = conj( fliplr(st) ); %时域匹配滤波为发射信号时间反褶再取共轭:h(t)=s*(-t)
s1 = conv(st,ht); %线性调频信号经过匹配滤波器后的输出(时域卷积)
N1 = N+N-1 ; %线性卷积后信号长度变为 N1+N2-1
t1 = linspace( -T/2 , T/2 , N1);
%% 频域匹配滤波1 (复制发射脉冲进行时间反褶并取共轭,计算补零DFT)
N2 = 2*N; %循环卷积长度 (N2应当≥N+N-1,其中弃置区位于长度大于N+N-1的部分)
t2 = linspace( -T/2 , T/2 , N2);
Hf1 = fftshift(fft(ht,N2)); %频域匹配滤波器
Sf2 = fftshift(fft(st,N2)); %频域信号
S2 = Sf2 .* Hf1; %频域乘积
s2 = ifft(S2);
%% 频域匹配滤波2(复制发射脉冲补零后计算FFT,再取共轭)
Hf2 = fftshift(conj(fft(st,N2)));
S3 = Sf2.* Hf2;
s3 = fftshift(ifft(S3));
%% 频域匹配滤波3(直接生成频域滤波器)
f_h = (-N2/2:N2/2-1)*Fs/N2;
Hf3 = exp(1i*pi*f_h.^2/K);
S4 = Sf2.*Hf3;
s4 = ifft(S4);
%% 绘图
% 时域
figure,plot( t*1e6, real(st) ),xlabel('t /us'),ylabel('幅度'),title('Chirp信号 实部');
figure,plot( t*1e6, imag(st) ),xlabel('t /us'),ylabel('幅度'),title('Chirp信号 虚部');
figure,plot( t*1e6, f*1e-6 ),xlabel('t /us'),ylabel('频率 /MHz'),title('Chirp信号 频率');
figure,plot( t*1e6, phase ),xlabel('t /us'),ylabel('相位 /rad'),title('Chirp信号 相位');
% 频域
figure,plot( freq*1e-6,abs(Sf) ),xlabel('f /MHz'),ylabel('幅度谱'),title('Chirp信号 幅度谱');
figure,plot( freq*1e-6,-pi*freq.^2/K+pi/4 ),xlabel('f /MHz'),ylabel('相位谱'),title('Chirp信号 相位谱');
% 时域匹配滤波
figure,plot( t1*1e6 , abs(s1) ),xlabel('t /us'),ylabel('幅度谱'),title('时域匹配滤波');
% 频域匹配滤波1
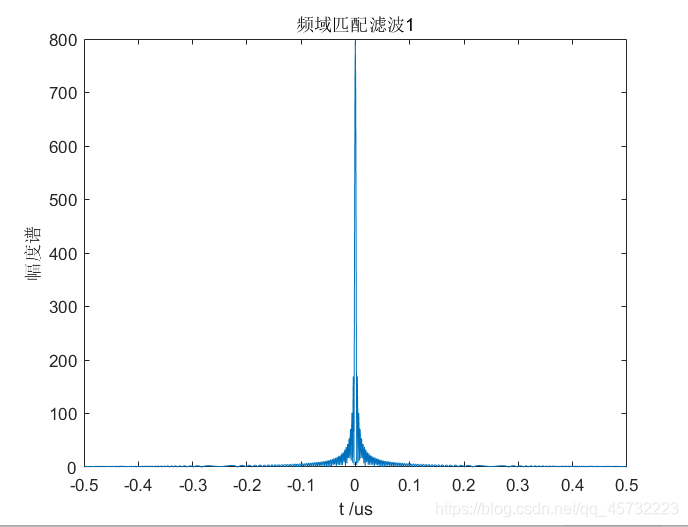
figure,plot( t2*1e6 , abs(s2) ),xlabel('t /us'),ylabel('幅度谱'),title('频域匹配滤波1');
% 频域匹配滤波2
figure,plot( t2*1e6 , abs(s3) ),xlabel('t /us'),ylabel('幅度谱'),title('频域匹配滤波2');
% 频域匹配滤波3
figure,plot( t2*1e6 , abs(s4) ),xlabel('t /us'),ylabel('幅度谱'),title('频域匹配滤波3');
- 结果:



10.2 利用匹配滤波器对回波信号进行脉冲压缩来测距
- 代码:
%%------------------------------------------------------------------------------------------------------------%%
%%说明:使用匹配滤波器进行脉冲压缩,matched_filter函数的输出包括未压缩和压缩的信号图形,以及在脉冲压缩中使用的线性调频信号%%
%%------------------------------------------------------------------------------------------------------------%%
function [y] =matched_filter(nscat,taup,b,rrec,scat_range,scat_rcs,winid)
%********* y: 归一化的压缩输出 **************%
%***** nscat: 目标个数 *********************%
%****** taup: 信号时宽,单位为s *************%
%********* b: 信号带宽,单位为Hz ************%
%****** rrec: 接收窗的大小,单位为m *********%
% scat_range: 目标的相对距离向量,单位为m ****%
%** scat_rcs: 目标的雷达截面积向量,单位为m^2 %
%***** winid: 决定了选用什么样的滤波器形式 ***%
%%%%% 时宽带宽积--time bandwidth product %%%%%
T_B_product=b*taup;
if(T_B_product<5)
fprintf('**********Time Bandwidth product is TOO SMALL**********')
fprintf('\nChange b and or taup');
return
end
c=3e8; %光速--speed of light
n=fix(5*taup*b); %采样点数--number of samples;函数fix():向零方向取整
%根据奈奎斯特采样定理及频率分辨率△f=fs/N的要求可以确定采样点数N的取值
%%%%% 初始化输入输出--initialize input,output %%%%%
x(nscat,1:n)=0;
y(1:n)=0;
%%%%% 确定合适的接收窗--determine proper window %%%%%
if(winid==0) %不加窗
win(1:n)=1;
win=win';
else
if(winid==1) %汉明窗
win=hamming(n);
else
if(winid==2) %带参数pi的凯泽窗
win=kaiser(n,pi);
else
if(winid==3) %旁瓣为-60dB的切比雪夫窗
win=chebwin(n,60);
end
end
end
end
%%%%%% 确保目标在接收窗内--check to ensure that scatters are within receive window %%%%%
index=find(scat_range>rrec);
if(index~=0)
fprintf('Error.Receive window is too large or scatters fall outside window');
return
end
%%%%% 计算采样间隔--calculate sampling interval %%%%%
t=linspace(-taup/2,taup/2,n);
LFM=exp(1i*pi*(b/taup).*t.^2); %载频为0的线性调频信号
figure(1);
subplot(2,1,1);
plot(t,real(LFM));
xlabel('时间/s');
ylabel('线性调频信号的实部');
grid on;
subplot(2,1,2);
sampling_interval=taup/n;
freqlimit=1/sampling_interval; %采样频率Fs=1/Ts
freq=linspace(-freqlimit/2,freqlimit/2,n);
plot(freq,fftshift(abs(fft(LFM))));
xlabel(' 频率/Hz');
ylabel('线性调频信号的幅度谱');
grid on;
for j=1:1:nscat
range=scat_range(j);
x(j,:)=scat_rcs(j).*exp(1i*pi*(b/taup).*(t+2*range/c).^2); %第j个目标的回波信号
y=x(j,:)+y; %实现对nscat个目标回波信号的叠加
end
figure(2);
plot(t,real(y),'m');
xlabel('相对延迟/s');
ylabel('未压缩回波');
grid on;
out=xcorr(LFM,y); %xcorr(x,y):互相关函数
out=out./n;
s=taup*c/2;
Npoints=ceil(rrec*n/s); %ceil():朝正无穷方向取整
dist=linspace(0,rrec,Npoints);
figure(3);
plot(dist,abs(out(n:n+Npoints-1)),'k');
xlabel('目标相对距离');
ylabel('压缩回波');
grid on;
end
-
结果:
-
2个目标的回波信号的匹配滤波
clear all;
close all;
clc;
%%调用matched_filter函数,观察结果,这两个目标回波是重叠的,不能被分辨,但是脉冲压缩后,这两个脉冲是完全分开的,即可以被分辨出来
nscat=2; %两个目标
taup=10e-6; %10us信号时宽
b=50.0e6; %50MHz脉宽
rrec=50; %50m的接收窗
scat_range=[15 25]; %目标的相对距离分别为15m、25米
scat_rcs=[1 2]; %目标的雷达截面积分别是1m^2和2m^2
winid=0; %不加窗
[y]=matched_filter(nscat,taup,b,rrec,scat_range,scat_rcs,winid);



- 3个目标的回波信号的匹配滤波
clear all;
close all;
clc;
%%%%%%%%%% 调用matched_filter函数观测3个目标相对距离为[10 75 120]m的结果 %%%%%%%%%%
nscat=3; %3个目标
taup=5e-6; %5us非压缩脉冲
b=100e6; %100MHz脉宽
rrec=200; %200m的处理窗
scat_range=[10 75 120]; %目标相对雷达的距离分别为10m、75m及120m
scat_rcs=[1 2 1]; %目标的雷达截面积分别是1m^2、2m^2及1m^2
winid=2; %凯泽窗
[y]=matched_filter(nscat,taup,b,rrec,scat_range,scat_rcs,winid);











 本文探讨了匹配滤波器在数字信号接收中的关键作用,通过频域和时域分析,详细解释了其设计原理、输出性能和在线性调频信号脉冲压缩中的实现方法。MATLAB仿真展示了如何利用匹配滤波器对回波信号进行有效脉冲压缩,以提高雷达测距精度。
本文探讨了匹配滤波器在数字信号接收中的关键作用,通过频域和时域分析,详细解释了其设计原理、输出性能和在线性调频信号脉冲压缩中的实现方法。MATLAB仿真展示了如何利用匹配滤波器对回波信号进行有效脉冲压缩,以提高雷达测距精度。
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








