【强化学习】基础离线算法：Q-Learning算法

最新推荐文章于 2025-03-08 10:05:04 发布

不去幼儿园

最新推荐文章于 2025-03-08 10:05:04 发布

阅读量2.1k

点赞数 127

分类专栏：强化学习（RL） # 单智能体强化学习【SARL】文章标签：算法人工智能强化学习 python 机器学习

本文链接：https://blog.csdn.net/qq_51399582/article/details/144207901

版权

强化学习（RL）同时被 2 个专栏收录

66 篇文章

订阅专栏

单智能体强化学习【SARL】

14 篇文章

订阅专栏

📢本篇文章是博主强化学习（RL）领域学习时，用于个人学习、研究或者欣赏使用，并基于博主对相关等领域的一些理解而记录的学习摘录和笔记，若有不当和侵权之处，指出后将会立即改正，还望谅解。文章分类在👉强化学习专栏：

【强化学习】- 【单智能体强化学习】（2）---《基础算法：Q-Learning算法》

基础算法：Q-Learning算法

[Python] Q-learning实现

一、概述

在强化学习中，Q-Learning 是一种基于值函数的强化学习算法。它通过学习一个状态-动作值函数（Q函数）来选择最优策略。Q-Learning 是一种 无模型（model-free） 的强化学习方法，意味着它不需要了解环境的动态（即转移概率和奖励函数），而只依赖于与环境的交互。

Q-Learning 的目标是通过不断地更新 Q 值，使得智能体能够选择在给定状态下能获 $( 0 \leq \gamma \leq 1 )$ 得最大累积奖励的动作。Q-Learning 的一个重要特点是，它保证在探索足够多的状态-动作对后，最终会收敛到最优策略。

二、Q函数的定义

Q-Learning 中，Q函数 $Q(s, a)$ 表示在状态 $s$ 下采取动作 $a$ 所能获得的期望回报。Q函数是 Q-Learning 的核心，通过对 Q 值的不断更新，最终得到最优的 Q 函数 $Q^*(s, a)$ 。

三、Q-Learning算法的核心思想

Q-Learning 的核心思想是通过贝尔曼方程来更新 Q 值。贝尔曼方程描述了某一状态-动作对的 Q 值与其后续状态-动作对之间的关系。

在 Q-Learning 中，更新公式为：

$Q(s_t, a_t) = Q(s_t, a_t) + \alpha \left( R_{t+1} + \gamma \max_{a'} Q(s_{t+1}, a') - Q(s_t, a_t) \right)$

其中：

$s_t$ 和 $a_t$ 分别是当前状态和当前动作。
$R_{t+1}$ 是智能体在执行动作 $a_t$ 后，从环境中获得的即时奖励。
$\gamma$ 是折扣因子，表示未来奖励的衰减程度 $( 0 \leq \gamma \leq 1 )$ 。
$\max_{a'} Q(s_{t+1}, a')$ 是状态 $s_{t+1}$ 下所有可能动作的最大 Q 值，代表智能体在下一状态下选择最优动作后的预期回报。 $R_{t+1}$
$\alpha$ 是学习率，控制每次 Q 值更新的步长。

通过这个公式，Q-Learning 在每个时间步 $t$ 都会根据当前的经验（状态、动作、奖励、下一状态）来更新 Q 值。随着学习的进行，Q 值逐渐收敛到最优 Q 值 $Q^*(s, a)$ ，从而得到最优策略。

四、Q-Learning算法的工作流程

初始化 Q 表：首先，我们初始化 Q 值表格，通常将所有状态-动作对的 Q 值初始化为零或小的随机值。
选择动作：在每个时间步，智能体基于当前的 Q 值选择一个动作。常见的选择策略有：
- 贪婪策略（Greedy Policy）：选择当前 Q 值最大的动作，即选择 $\max_a Q(s_t, a)$ 。
- ε-贪婪策略（ε-greedy Policy）：以 $1-\epsilon$ 的概率选择 Q 值最大的动作，以 $\epsilon$ 的概率随机选择其他动作（探索新的状态），避免陷入局部最优。
执行动作并更新 Q 值：智能体根据选择的动作与环境交互，获得奖励 $R_{t+1}$ 和下一个状态 $s_{t+1}$ ，然后根据 Q-Learning 的更新公式更新 Q 值。
重复步骤2和步骤3：直到达到某个终止条件（例如，达到最大步数或者 Q 值收敛）。

五、Q-Learning 算法的推导

Q-Learning 的更新公式来自于 贝尔曼最优方程（Bellman Optimality Equation），它为求解最优值函数提供了递归关系。假设 $Q^*(s, a)$ 是最优状态-动作值函数，即在每个状态下，选择最优动作可以获得最大回报。根据贝尔曼最优方程，我们有：

$Q^(s, a) = \mathbb{E}{s'} \left[ R{t+1} + \gamma \max_{a'} Q^(s', a') \right]$

这表示，某一状态-动作对的 Q 值等于当前奖励 $R_{t+1}$ 加上未来状态 $s'$ 下，采取最优动作 $a'$ 所得到的最大预期回报。

通过与实际更新公式的对比，Q-Learning 通过贝尔曼方程递归地更新 Q 值，使得 Q 值逐渐逼近最优值 $Q^*(s, a)$ 。

六、Q-Learning 的收敛性

Q-Learning 算法具有 收敛性，即在所有状态-动作对的 Q 值都经过足够多的更新后，Q-Learning 会收敛到最优的 Q 值 $Q^*(s, a)$ 。这一收敛性基于以下条件：

充分探索：每个状态-动作对都被充分探索。
学习率衰减：学习率 $\alpha$ 随着时间逐渐减小，确保 Q 值能够稳定下来。

[Python] Q-learning实现

下面代码实现了一个经典的 Q-learning 强化学习算法，用于训练一个智能体在一个简单的环境中寻找从左到右的目标（状态从0到19，目标在19）。智能体的任务是通过向左或向右移动来最大化累积奖励。

项目代码我已经放入GitCode里面，可以通过下面链接跳转：🔥

【强化学习】--- Q-Learning算法

后续相关单智能体强化学习算法也会不断在【强化学习】项目里更新，如果该项目对你有所帮助，请帮我点一个星星✨✨✨✨✨，鼓励分享，十分感谢！！！

若是下面代码复现困难或者有问题，也欢迎评论区留言。

"""《Q-learning算法实现》
    时间：2024.12
    作者：不去幼儿园
"""
import numpy as np  # 导入NumPy库，用于数值计算
import pandas as pd  # 导入Pandas库，用于数据结构操作
import matplotlib.pyplot as plt  # 导入Matplotlib库，用于绘制图形
import time  # 导入time库，用于控制程序暂停时间

参数设置

ALPHA = 0.1  # 学习率，决定每次Q值更新的幅度
GAMMA = 0.95  # 折扣因子，决定未来奖励的权重
EPSILION = 0.9  # epsilon-greedy策略中的探索概率，控制随机选择动作的比例
N_STATE = 20  # 状态空间的大小，表示状态的数量
ACTIONS = ['left', 'right']  # 可用的动作集合，左移和右移
MAX_EPISODES = 200  # 最大训练回合数
FRESH_TIME = 0.1  # 每步之间的时间间隔，用于渲染环境

构建Q表

# 构建Q表，Q表存储每个状态-动作对的Q值
def build_q_table(n_state, actions):
    q_table = pd.DataFrame(
        np.zeros((n_state, len(actions))),  # 创建一个形状为(n_state, len(actions))的全零矩阵
        np.arange(n_state),  # 状态的行索引为0到n_state-1
        actions  # 动作的列索引为'left'和'right'
    )
    return q_table  # 返回Q表

选择动作

# 选择当前状态下的动作
def choose_action(state, q_table):
    # epsilon-greedy 策略
    state_action = q_table.loc[state, :]  # 获取当前状态下所有动作的Q值
    if np.random.uniform() > EPSILION or (state_action == 0).all():  # 探索（随机选择）或当Q值全为0时
        action_name = np.random.choice(ACTIONS)  # 随机选择一个动作
    else:  # 利用（选择Q值最大的动作）
        action_name = state_action.idxmax()  # 选择Q值最大对应的动作
    return action_name  # 返回选择的动作

环境反馈

# 获取环境反馈，依据当前状态和所选动作返回下一个状态和奖励
def get_env_feedback(state, action):
    if action == 'right':  # 如果选择了向右的动作
        if state == N_STATE - 2:  # 如果已经到达倒数第二个状态
            next_state = 'terminal'  # 终止状态
            reward = 1  # 到达终止状态时给予奖励1
        else:
            next_state = state + 1  # 否则，状态右移
            reward = -0.5  # 每步奖励为-0.5
    else:  # 如果选择了向左的动作
        if state == 0:  # 如果已经到达最左端
            next_state = 0  # 保持在状态0
        else:
            next_state = state - 1  # 否则，状态左移
        reward = -0.5  # 每步奖励为-0.5
    return next_state, reward  # 返回下一个状态和奖励

更新环境状态

# 更新环境的状态并打印出来
def update_env(state, episode, step_counter):
    env = ['-'] * (N_STATE - 1) + ['T']  # 创建一个状态列表，其中T表示目标终止状态
    if state == 'terminal':  # 如果状态是终止状态
        print("Episode {}, the total step is {}".format(episode + 1, step_counter))  # 输出当前回合和步数
        final_env = ['-'] * (N_STATE - 1) + ['T']  # 终止状态时的环境状态
        return True, step_counter  # 返回终止状态和步数
    else:
        env[state] = '*'  # 将当前状态位置标记为*表示智能体所在的位置
        env = ''.join(env)  # 将状态列表转为字符串显示
        print(env)  # 打印当前环境状态
        time.sleep(FRESH_TIME)  # 暂停FRESH_TIME秒以控制显示速度
        return False, step_counter  # 返回非终止状态和步数

Q-learning算法实现

# Q-learning算法实现
def q_learning():
    q_table = build_q_table(N_STATE, ACTIONS)  # 构建Q表
    step_counter_times = []  # 用于存储每个回合的步数
    for episode in range(MAX_EPISODES):  # 遍历每个回合
        state = 0  # 每个回合从状态0开始
        is_terminal = False  # 是否到达终止状态的标志
        step_counter = 0  # 步数计数器
        update_env(state, episode, step_counter)  # 更新环境并显示
        while not is_terminal:  # 如果没有到达终止状态
            action = choose_action(state, q_table)  # 选择动作
            next_state, reward = get_env_feedback(state, action)  # 获取环境反馈
            next_q = q_table.loc[state, action]  # 获取当前状态-动作对的Q值
            if next_state == 'terminal':  # 如果到达终止状态
                is_terminal = True  # 标记为终止状态
                q_target = reward  # 目标Q值为奖励值
            else:  # 如果没有到达终止状态
                delta = reward + GAMMA * q_table.iloc[next_state, :].max() - q_table.loc[state, action]  # 计算TD误差
                q_table.loc[state, action] += ALPHA * delta  # 更新Q值
            state = next_state  # 更新状态
            is_terminal, steps = update_env(state, episode, step_counter + 1)  # 更新环境并显示
            step_counter += 1  # 步数+1
            if is_terminal:  # 如果到达终止状态
                step_counter_times.append(steps)  # 记录回合的步数
    return q_table, step_counter_times  # 返回更新后的Q表和每个回合的步数列表

程序入口

# 程序入口
if __name__ == '__main__':
    q_table, step_counter_times = q_learning()  # 运行Q-learning算法
    print("Q table\n{}\n".format(q_table))  # 打印最终的Q表
    print('end')  # 打印训练结束信息

    # 绘制每回合步数的图表
    plt.plot(step_counter_times, 'g-')  # 以绿色线条绘制步数
    plt.ylabel("steps")  # 设置Y轴标签为"steps"
    plt.show()  # 显示图表
    print("The step_counter_times is {}".format(step_counter_times))  # 打印每个回合的步数

[Results] 运行结果

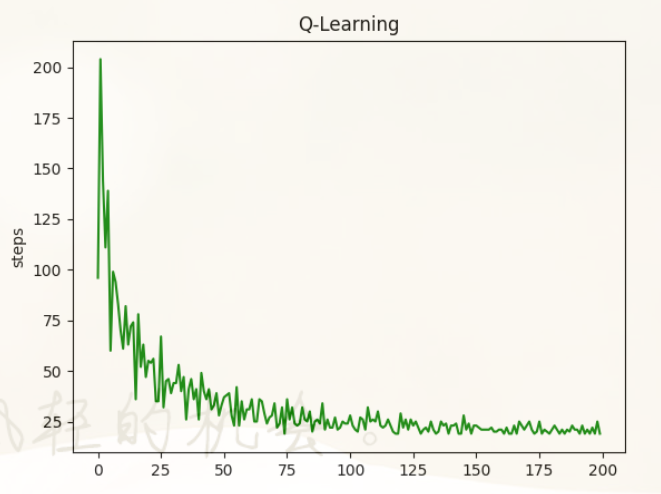
[Content] 算法内容

状态空间：智能体有20个状态（从0到19），目标状态是状态19。
动作空间：智能体可以选择两个动作："left"（向左）和 "right"（向右）。
奖励机制：每一步都会受到-0.5的惩罚，只有在到达目标状态时（状态N_STATE-2），智能体会获得+1的奖励。
Q-learning：智能体通过 epsilon-greedy 策略来选择动作，以平衡探索和利用。Q值根据 TD-error 更新，学习率为 ALPHA，折扣因子为 GAMMA。

[Notice] 注意事项：

状态和动作空间的大小：此实现仅适用于较小的状态和动作空间，状态空间非常大时需要考虑更高效的策略。
Q值更新：Q-learning 算法通过不断更新 Q 表来改进策略，但每个状态-动作对的 Q 值更新会比较缓慢，可能需要更多回合来收敛。
终止条件：训练通过状态 'terminal' 来标识终止状态，若达到目标状态，即进入终止状态，智能体会停止该回合的学习。
学习率与折扣因子：学习率和折扣因子需要根据实际问题进行调优，以保证学习过程稳定且高效。

# 环境配置
Python                  3.11.5
torch                   2.1.0
torchvision             0.16.0
gym                     0.26.2

七、优缺点

优点：

简单易实现：Q-Learning 算法简单，易于实现，并且不需要对环境的模型做任何假设。
无模型方法：Q-Learning 是一个无模型的方法，意味着它不需要环境的转移概率和奖励函数。
保证收敛性：在充分探索且适当设置学习率的情况下，Q-Learning 保证最终能够收敛到最优策略。

缺点：

大规模状态空间问题：对于大型状态空间或连续状态空间，Q-Learning 需要保存一个巨大的 Q 值表，这在实际应用中不可行。为了解决这个问题，通常会使用 深度Q网络（DQN） 来进行近似。
探索和利用的平衡问题：Q-Learning 需要在探索新的动作和利用已学得的知识之间做平衡，特别是当状态空间较大时，探索的效率和效果是一个挑战。