三维点云处理第三章（1）--Clustering（聚类）

相似的东西放在一起，看作一个类。聚类涉及到的相关知识很多。

线性代数：谱聚类的物理意义，对一个矩阵SVD的物理意义，就是把它分解成两个旋转矩阵，加一个缩放矩阵，A在这里是一个对称矩阵，所以两个旋转矩阵是一样的，所以就可写成下面这种形式，进一步拆开就有特征值，以及uu正交的矩阵。

 这里是瑞利熵，它同样可以通过SVD的物理原理来理解，既然一个向量，同样可以分解成两个旋转矩阵，加一个缩放矩阵。缩放矩阵其实是一个对角矩阵，对角线放的就是在每一个轴上我要缩放多少，旋转矩阵不会对一个向量的长度做出改变的，所以瑞利熵最大可以取多少，最小可以取多少，就取决于这个A里面的缩放矩阵。概率l论基础知识:两个事件X、Y,P(x,y)就是两个事件发生的概率，两个事件可以是离散的、连续的、也可以是离散加连续的。连续情况下，，边缘分布和全概率公式很相似。如右下图，x\y的分布，颜色越白越亮的部分，说明x,y取这个值的概率会更大。想得到x就把y给积分，想得到y就把x积分。

 离散情况下同理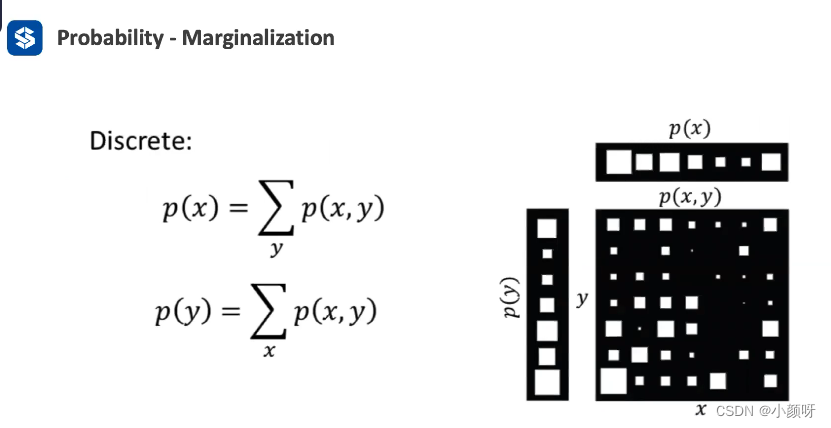

 那么做完积分后，这还是不是一个合法的概率分布呢（也就是概率总和等于1）？一定是。因为我对积分后得到的x概率做一次求和，它一定会等于1。

但是，在条件概率情况下（之前是不管其中一个，只要另一个的全概率），也就是假如我先知道y是某一个确定已知的值，比如y = y1或y = y2，那么此时就出现条件概率的分布，在这种条件下，x是一种什么样的分布呢？其实现在就只需要考虑y = y1那一条线上的值就可以了，就可以得到该情况x的分布。但此时这个切片并不是一个合法的分布，因此我们需要对它做一个归一化，如下式。也就是贝叶斯公式。

 扩展到更多的维度，如下式。

 图论知识：图论里面的图有两种，一种是有向图，一种是无向图。有向图由一系列的节点和一系列的边组成，如图右上角。每一个节点代表每一个随机变量，每一条边代表两个随机变量之间的联系。它们的分布就可以写成，也就是前面提到的条件概率。如果两个变量没有关系，那么。

 无向图的变量之间的联系是没有方向的。就像两个城市，以及中间的一条路。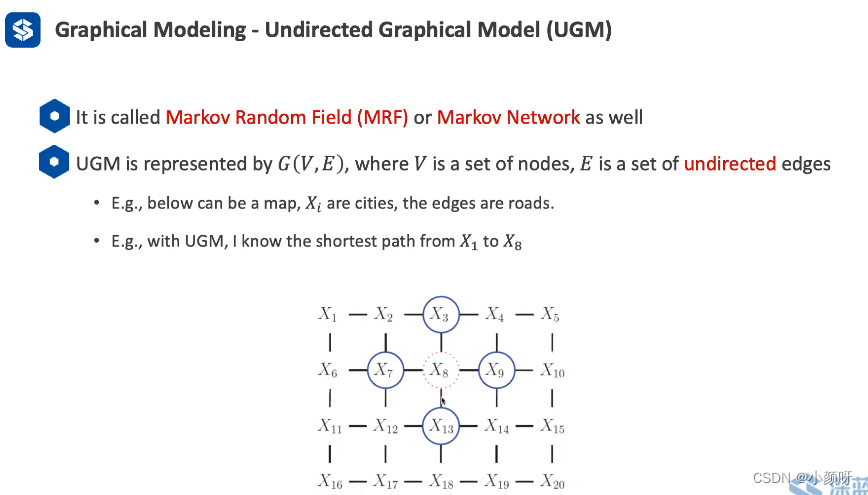

 优化方法：拉格朗日求解法。想优化一个二元函数，但做优化时有一个限制，就是要求，那么一定有（一阶求导符号），可以取到最大值。

 数学上，其实就是拉格朗日求法。先写这样一个式子,然后让其对每一个变量求一阶导并令为0，也就是，再求解,如图所示。