GaN HEMT器件在栅极偏置下的寿命模型

一、GaN器件高温栅偏应力失效机理

应力研究分为动静态，分别对应不同的研究模型

本节重点介绍温度应力对器件失效机理的影响，主要是栅偏应力对器件失效机理的影响，称之为HTGB（High Temperature Gate Bias）研究。从栅压应力大小、栅压应力时间等不同的实验条件出发，研究p-GaN HEMT器件相关电学参数的稳定性（也即高温偏置下的可靠性）问题。通过器件电学参数的退化结果，对其失效机理进行研究和分析。对不同的栅压应力及作用时间来说，不同电学参数的退化程度不一定相同，从而能够反映不同的失效机理。主要分析的电学参数包括阈值电压（Vth）、导通电阻（Ron）、栅极漏电流（Igss）、关态漏电流（Idss）以及电容等。

进行HTGB考核时，将HV1（D）端子（即漏极）与GND端子进行短接并接地，将HV2 （G）端子（即栅极）接输入电源正极，如图1.1所示。

图1.1 HTGB 考核板

为进行动态栅偏置应力的研究，需要搭建测试平台。为模拟功率p-GaN HEMT在半桥电路中的续流工作状态，搭建了续流应力测试平台，使p-GaN HEMT的栅偏置交替工作Vgs>0,Vgs<0和Vgd>0的状态，如图1.2所示。在应力过程中， 将p-GaN HEMT器件作为续流器件，器件工作在反向导通状态，即工作在第三象限，类似于 MOSFET的体二极管特性器件的反向开启电压随栅源电压偏置Vgs的不同而变化，Vgs越负，反向开启电压就越大，反向工作电流越大，随之源漏电压(Vsd)越大且Vgd 越大。随着DUT工作电流的变化，DUT的栅偏置出现动态变化，DUT的Vgs>0,Vgs<0和Vgd>0交替出现。在测试过程中，应该控制开关器件的脉冲信号，使得DUT的工作电流间歇出现，防止DUT过热而带来额外的温度影响，影响器件退化机理的研究。

为了验证动态栅偏置应力导致的电学参数退化机理，改变了器件的续流应力的条件，如表1.1

表1.1 动态栅应力条件

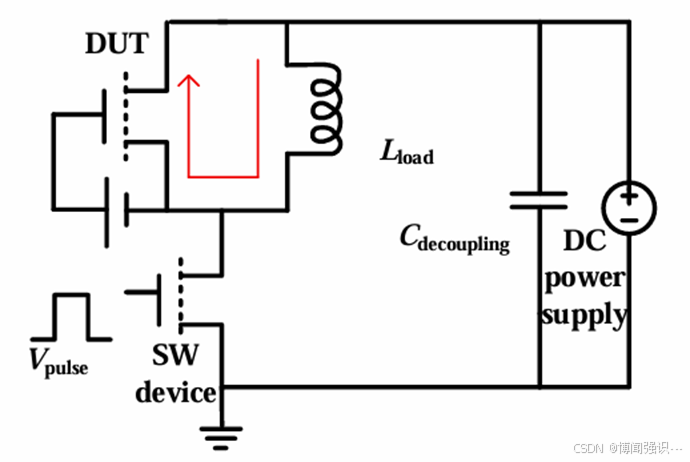
图1.2 续流应力电路原理图

本节参考文献：

[1]辛树轩.p-GaN HEMT器件高温偏置可靠性研究[D].东南大学,2022.DOI:10.27014/d.cnki.gdnau.2022.004027.

[2]李胜.增强型功率p-GaN HEMT可靠性研究[D].东南大学,2022.DOI:10.27014/d.cnki.gdnau.2022.000214.

[3]J. He, J. Wei, S. Yang, M. Hua, K. Zhong and K. J. Chen, "Temperature-Dependent Gate Degradation of p-GaN Gate HEMTs under Static and Dynamic Positive Gate Stress," 2019 31st International Symposium on Power Semiconductor Devices and ICs (ISPSD), Shanghai, China, 2019, pp. 295-298, doi: 10.1109/ISPSD.2019.8757574.

二、GaN器件温度应力寿命模型选取

要构建寿命模型，首先要明确与器件的寿命相关的各种影响因子。本试验重点研究对象是高温偏置条件下的器件寿命特性，因此，首要影响因子是温度应力；其次要研究的影响因子则是电应力。那么，要对多个影响因子展开研究，应采取控制变量法，先对单因子变量进行研究，再对多个影响因子的叠加效应进行研究。

加速寿命试验的方式有很多种，而不同的加速方式满足不同的寿命加速方程，如表2.1所示

表2.1 加速寿命模型类别

由表2.1可知，寿命加速模型与所施加的应力种类息息相关。Arrhenius模型适用于单温度加速应力，逆幂率模型适用于单电压加速应力，Eyring模型则适用于温度和电压混合加速应力。本试验中高温偏置应力即温度应力与电压应力的叠加，应选取Eyring模型。但是，Eyring模型仅仅是由经验得出的公式，该公式的形式是否准确还有待验证。因此，必须通过试验的方式对GaN HEMT器件的失效时间与所加应力之间的关系进行推导和验证。

按照控制变量法，应首先从温度应力对器件寿命的影响出发进行加速寿命试验。 需要明确的是，由于GaN HEMT器件通常工作在高压条件下，在进行温度应力加速试验时，应保持器件处于固定的工作电压（即漏压或栅压保持不变）的条件下，然后通过温度的改变，研究温度应力的变化对器件失效时间（即寿命）的影响，否则加速寿命试验脱离了真实的工作条件，也就失去了研究意义。

其次，在进行温度应力加速寿命试验时，要保证在试验条件范围内，影响因子仅仅是改变了器件的失效速度，而不改变器件的失效机理，否则在同一加速方程下，加速因子将产生质的变化，所求得的加速系数也就失去了意义。因此，在进行试验时，还应保证所加应力处在同一失效机理机理模式下。这一点将在加速寿命试验数据的基础上进行证实。

寿命模型的建立要用到Weibull分布（威布尔分布），它是一种概率密度分布模型。根据传统经验，产品的寿命分布函数有指数分布、对数分布、正态分布以及接下来要研究的 Weibull分布。由应力敏感参数退化量决定的 GaN HEMT 器件的寿命规律符合最弱环节模型，即局部失效导致整体失效的模型，而Weibull分布函数模型的基础就是最弱环节模型。

图2.1 浴盆曲线示意图

不同失效阶段对应着不同的失效诱因，分别是器件固有缺陷、外界偶然因素和器件长期处于应力环境发生老化所导致。而我们所要重点研究的就是器件的老化规律，因此应排除前两种因素的干扰。Weibul分布的概率分布函数的一般形式如式2-1所示。

那么，Weibull分布的概率密度函数则由式 2-1求导可得

 Weibull分布模型具有三个关键参数，分别是𝛾参数（位置参数）、m参数（形状参数）、𝜂参数（尺度参数）寿命模型的建立需要根据试验数据求解出Weibull分布的概率密度函数的三个参数。一般的，对半导体器件的寿命进行预测时，器件可能从一开始（即t=0时刻）就发生失效，因此，在本试验的研究中，位置参数𝛾取0。

此时对应的概率分布函数可变形为：

那么此时的概率密度函数为：

当𝑡=𝜂时，𝐹(𝑡)=63.2%，是一个常数，与形状参数无关。称此时的t值为该模型的特征寿命

那么，关于t-F（t）的坐标曲线和关于x-y的坐标曲线即可通过实际试验得到的数据在同一平面中绘制出来，如图2.2所示(示例)。

图2.2 威布尔分布曲线示例

时间-失效率关系曲线代表了一批器件在达到某一失效率时对应的，即可获得器件在某应力条件下的特征寿命。

在单温度应力条件下，器件从正常状态过渡到失效状态，其根本原因在于某些电学参数发生了退化。根据化学家Arrhenius在1880年提出的Arrhenius模型，反应速率与温度的关系满足式2-9：

其中，EA表示器件的失效激活能；k表示玻尔兹曼常数（8.617×10−5𝑒𝑉/𝐾），A表示加速系数（也就是在该应力作用条件下失效快慢的斜率）

对温度加速应力而言，加速寿命试验通常在三种不同但较高的温度下进行，通过记录器件的失效率，来确定三种温度应力下的具体失效时间。因此，该试验又称为“三温（3T）”寿命试验。

由式2-9变形得

 

由此可见，ln𝑡与1/𝑇 满足线性关系。

在式2-13中，称𝑛为温度应力加速系数，𝑚为温度加速寿命方程的常系数。

根据前述器件在不同温度下的特征寿命，能够得到特征寿命-温度应力关系图，也称为器件与应力之间的特征寿命图，如图2.3所示。

图2.3 应力-特征寿命分布图示例

该拟合曲线的斜率即温度应力加速系数n，截距即常系数m。

这里我们还需要进行应力敏感参数的确定(在下节预测试方案中给出)以及失效激活能EA的提取，确定了器件的失效激活能，即确定了寿命方程中的加速系数，从而能够推导出寿命-温度应力方程。但是，这样求得的失效激活能并不准确，因为寿命与温度应力之间并非严格遵循简单的数学关系，根据任意两点所确定的失效激活能不一定准确，而是需要通过大量试验数据进行二者之间关系的拟合。只有根据一系列散点图拟合出的线性表达式才更加准确并符合实际失效规律，因此，有必要在不同应力组别中设置一定数量的器件进行加速寿命试验。

本节参考文献：

[1] 茆诗松.加速寿命试验的加速模型[J].质量与可靠性,2003(02):15-17.

[2] 王乔方,郑万祥,王冲文,刘剑,罗瑞,赵远荣.基于威布尔分布的某半导体器件贮存寿命分布规律初探[J].红外技术,2020,42(11):1077-1080.

[3] 贾骄.GaAs pHEMT可靠性测试研究[D].电子科技大学,2014.

[4] R. Pazirandeh, J. Wurfl and G. Trankle, "Comparison of DC measurement methods to determine GaN HEMT reliability," 2009 Reliability of Compound Semiconductors Digest (ROCS), Greensboro, NC, USA, 2009, pp. 41-51.

[5]辛树轩.p-GaN HEMT器件高温偏置可靠性研究[D].东南大学,2022.DOI:10.27014/d.cnki.gdnau.2022.004027.

三、GaN器件栅极反向偏置应力下的寿命模型及测试方案的选择

3.1测试标准与规范

3.1.1 测试样品的审查和选择

被选的测试器件必须能代表绝大部分的器件。如果要对特定应用的器件进行测试，那么对样品的审查不能比装载产品时的审查还要严格。对于比较通用的器件，必须对样品进行一个热阻和可靠性审查，以减少潜在的早期失效，这样寿命测试时便有足够多的样品能存活下来，以便进行有效的寿命计算

3.1.2 电学和热学特征测试

每一个将要进行寿命测试的器件（以及控制样品）在它们的寿命测试过程中，必须进行电学特征测试。被测参数应该基于器件的电学功能，除此之外，每个参数必须有一个失效的标准，并且在寿命测试过程中各个参数必须分别用同一个方法去测量。有时候MMIC产品的设计将会妨碍某些参数的测量。 另外被测参数必须包含：Idss漏电流密度为1mA每毫米沟道宽度时的漏栅电压，应力中用到的偏压，工作电流，跨导，以及S参数。功率器件和通用器件必须有1dB的压缩点，如果可行的话，需测量栅电流，对低噪声器件必须测量噪声图像数据。

器件热阻可以采用红外扫描或者其他方法测试。在该标准发行之后，模型技术将被广泛采纳用于热阻的测试。实验数据当至少被至少10%的器件证明无误时，就可被采纳。 如果由器件的电源耗散引起的测量偏差不超过５摄氏度时,这个热阻的平均值就可用于所有的器件；如果不满足这个条件，那么必须测量每个器件的相对热阻，以确定在实际工作中器件管壳和沟道温度的不同。

3.1.3 测试环境温度和其他操作条件的选择

最高的稳定测试应力温度必须在器件的预期寿命中位值至少是100小时的条件下才能应用。如果测试时间间隔太长，那么最低温度时的寿命将是一个不合理的时间或者各寿命测试的温度间隔将会太近而使得不能做出正确的推断。 如果测试采用是步进应力的方法，那么最高的稳定应力测试平台温度至少要比在 24小时内产生50%失效率的步进应力测试平台温度低20℃。 另外，如果已知器件的主要失效机理会因为器件温度高于正常工作温度而改变，那么器件的寿命测试必须在低于正常工作温度下进行。

测试至少需要三个稳定应力温度。第二个温度至少要比最高温度低15℃， 第三个温度至少要比第二个温度低15℃。另外，如果三个测试平台的温度都高于200℃，那么第四份器件样品必须在高于器件最高工作温度50℃的测试平台上进行测试(如果器件的最高工作温度未标明，则测试平台的温度取150℃)，且测试至少要保持2000小时，以鉴明关于器件工作范围的推断的有效性。在这个温度下，我们期望器件很少失效，与温度不同的是，应力还可用于器件的加速退化。

虽然应力不可作为失效的激活能但是器件的寿命依赖于工作电压、电流及其它与器件有关的因素，可以通过让器件工作于高于正常工作的应力条件下而加速测试过程。除了每个变量与器件寿命的关系函数不同之外。其它的数据分析都与温度一样。当使用过量的电应力时，器件的温度可能改变得足够多，以致于影响器件的寿命，为保证FET的沟道温度一致，每个过载电应力测试集必须有不同的环境温度。

3.1.4 失效标准

失效标准必须表示成一个参数的改变范围的形式，如表3.1，就必须声明。 除非特殊声明，测试过程中FET的漏电压和栅电压必须保持恒定，而电流在保持其它测试条件的前提下改变。测试温度必须是常数。如下表所示

表3.1 JEDEC功率器件失效标准

电流(Idss)	+/-20%
跨导	+/-20%
射频小信号增益	+/-1dB
功率附加效率	初始值的+/-20%
1dB压缩点输出功率	-2dB(仅适用于功率器件)

3.2 测试方案

根据前文分析，加速寿命试验首先要进行应力敏感参数的确定，该过程也可以称之为加速寿命试验的预实验。 选取一组待测器件，在Vds_test、T_test恒定应力作用下，测试5分钟，取出并记录器件各项电学参数（如Vth、Ron、Igss、Idss等）的变化；继续测试，至10分钟时，取出并记录器件的各项电学参数的变化；继续测试，直至测试时间达到30min，逐一记录器件的各项电学参数的变化。将实验结果填入表3.2。

表3.2 电学参数退化量记录表(预测试)

应力时间	Vth	Igss	Idss	Ron
初始值	V1	Ig1	Id1	R1
5min	V2	Ig2	Id2	R2
15min	V3	Ig3	Id3	R3
30min	V4	Ig4	Id4	R4
退化量百分比	∆1%	∆2%	∆3%	∆4%

根据器件各电学参数的实测值，计算出每个参数对应的退化量，选取退化百分比最大的参数作为应力敏感参数M，后续测量均选取此参数作为失效判断的标准。

根据实验条件和实验时长要求，作出如下规定：应力敏感参数M的变化量超过20％（不包括20％）时，该器件即为失效。

将器件等分为3组，分别为G1、G2、G3，每组5个，共计15个。

先确定负栅压条件下GaN HEMT器件的栅极漏电流。

图3.1 负栅压条件下某GaN cascode器件的栅极漏电流(示例，按实际测试改)

测试方案：在常规测试应力条件下（取T=100℃，Vgs =-V0），根据器件栅极漏电流的测试曲线，-V0为栅极应力区间的分界，当Vgs>-V0，器件Igss随Vgs的递减缓慢增长，此时电流传输以扩散电流及电场导致的漂移电流为主；当Vgs<-V0 V，器件Igss随Vgs的递减呈指数增长，此时隧穿电流为电流传输的主导。对所有待测器件进行应力预测试，测试时间为10min，观察器件状态并记录应力敏感参数M的变化，将失效器件筛除。该操作为偶然失效排查，排除早期失效或偶然失效的器件。拟选取的温度加速应力分别为：T1=375K（100℃，G1 组）、T2=425K（150℃，G2 组）、 T3=475K（200℃，G3 组）。

每组器件的测试时间共计300h。

取G1组器件，测试条件：T1=375K。

连接好测试电路，设置所加应力到达规定条件，开始进行测试计时，并按照对数时间曲线记录各时刻被测器件的应力敏感参数M的值。

当测试进行到12h时，取出被测器件，待器件结温恢复至室温时记录M的值；

继续施加该应力条件，当测试时间达到24h时，按照前述条件记录M的值； 记录测试进行到48h时M的值；

……

如此循环，直至测试时间达到300h。

仿照G1组器件测试流程，对G2、G3组器件进行测试和记录，如表3.3所示。

表3.3 不同温度应力下器件寿命预测(三温测试)

温度应力(个)	被测器件数(个)	试验时间（h）	参数退化率（%）	特征寿命（h）
375	5	300	∂1	T1
425	5	300	∂2	T2
475	5	300	∂3	T3

根据三组加速寿命试验的退化情况，计算失效率。在有限的试验时间内，器件可能发生失效，也可能未达到失效标准。但是，可以在已获得的退化数据基础上拟合出退化率-时间关系曲线，从而合理预测出当器件的退化率达到失效标准时所需要的应力作用时间，也即失效时间。同一批次器件中的不同个体在相同应力下的失效时间可能不一致，那么，根据应力-失效时间散点图，可以作出GaN HEMT器件在某应力条件下的失效率F（t）-失效时间（t）关系散点图，并进行拟合，得到失效率F（t）-失效时间（t）关系曲线。

如果三组应力下的失效率F（t）-失效时间（t）曲线近似平行，也就是说，在该试验的温度范围内，GaN HEMT器件的失效机理基本保持一致，说明实验数据有效。根据式2-8求得器件在不同应力下的特征寿命𝜂。

最后依据特征寿命值与温度应力的对应关系，在坐标系中绘制出特征寿命-温度应力关系散点图，并进行拟合，就能得到特征寿命图。

那么，根据拟合曲线，即可以得到寿命加速方程中的各系数，并计算得到器件的失效激活能，从而确定具体的寿命加速方程形式：

由寿命加速方程，能够推出在给定的温度应力下，p-GaN HEMT器件在该应力条件下正常工作的时间，即器件的寿命。

例如，在室温下（T=300K，即25℃时），某特定GaN HEMT器件的特征寿命值为

也就是说，在某一批次GaN HEMT器件中，在失效率不高于63.2%的前提下，该批次器件大约能够正常工作的时间不低于  

下面几个表格为测试需要测量的所有参数

表3.4 加速寿命预实验器件各电学参数变化量

应力时间	Vth(V)	Igss(μA)	Idss(μA)	Ro(mΩ)
应力前
应力1h
变化量

表3.5 批次GaN HEMT器件某电学参数M随应力时间退化表（T=375K，Vgs=-V0V）

器件编号	A1#	A2#	A3#	A4#	A5#
初始值
应力12h
应力24h
应力48h
应力72h
应力100h
应力150h
应力200h
应力250h
应力300h

表3.6 批次GaN HEMT器件某电学参数M随应力时间退化表（T=425K，Vgs=-V0V）

器件编号	A6#	A7#	A8#	A9#	A10#
初始值
应力12h
应力24h
应力48h
应力72h
应力100h
应力150h
应力200h
应力250h
应力300h

表3.7 批次GaN HEMT器件某电学参数M随应力时间退化表（T=475K，Vgs=-V0V）

器件编号	A11#	A12#	A13#	A14#	A15#
初始值
应力12h
应力24h
应力48h
应力72h	(可能失效)
应力100h	(先存放着)
应力150h
应力200h
应力250h
应力300h

表3.8 批GaN HEMT器件某电学参数M随应力时间退化表（T=375K，Vgs=-V0-2V）

器件编号	A16#	A17#	A18#	A19#	A20#
初始值
应力12h
应力24h
应力48h
应力72h
应力100h
应力150h
应力200h
应力250h
应力300h

表3.9 批GaN HEMT器件某电学参数M随应力时间退化表（T=375K，Vgs=-V0-4V）

器件编号	A21#	A22#	A23#	A24#	A25#
初始值
应力12h
应力24h
应力48h
应力72h
应力100h
应力150h
应力200h
应力250h
应力300h

表3.10 批GaN HEMT器件某电学参数M随应力时间退化表(T=375K，Vgs=-V0-6V)

器件编号	A26#	A27#	A28#	A29#	A30#
初始值
应力12h
应力24h
应力48h
应力72h
应力100h
应力150h
应力200h
应力250h
应力300h

表3.9 批GaN HEMT器件某电学参数M随应力时间退化表（T=375K，Vgs=-V0-8V）

器件编号	A31#	A32#	A33#	A34#	A35#
初始值
应力12h
应力24h
应力48h
应力72h
应力100h
应力150h
应力200h
应力250h
应力300h

处理上述数据可以提取的参数：(失效激活能、电压加速因子，经计算可得这一批次任意器件的预测寿命)，然后再将实测验证与预测寿命进行验证

3.3 高温栅极反偏加速寿命模型的确定

艾琳模型虽然是经验公式，但符合高温偏置应力下的寿命模型。

根据已选取的加速寿命模型，将加速寿命方程中的系数重新进行定义，定义系数φ1为温度加速因子，定义系数φ2为电压加速因子。

采用控制变量的方式，将式（3-4）变形为

改变电压应力大小，就得到关于电压应力的特征寿命-电压应力关系曲线，对该曲线进行拟合，即可求出电压加速因子φ2。

改进措施：其中在文献[4]和文献[6]中提出的器件工作结温问题，即器件工作时结温与外壳温度不一致，这与热阻有关，计算公式在文献[4]中表示为：器件的结温确定由两部分组成，即芯片耗散功率产生的温升和管壳上面的温度 （热沉的温度），结温（沟道温度）的确定公式为

                       (3-13)

公式中,Rth为器件的热阻，Tc为管壳温度，VDS为源漏电压, IDS为器件漏极。而文献[6]认为热阻Rth不是固定不变的，而是在不同的区域有不同的值，并进行了热阻模型的建立，模型可根据此进行改进。

本节参考文献：

[1] JEDEC,JESD22A-108,Temperature,Bias, and operating life[S]，JEDEC,01 Nov, 2010；

[2] JEDEC,JEP118A, Guidelines for GaAs MMIC and FET life testing[S],JEDEC,25 Jan 1993；

[3] 沈雨桐.宽禁带半导体功率器件关态应力退化机理及寿命建模研究[D].西安电子科技大学,2023.DOI:10.27389/d.cnki.gxadu.2023.003409.

[4]刘曦.GaN HEMT可靠性及寿命评估研究[D].西安电子科技大学,2013.DOI:10.27389/d.cnki.gxadu.2013.000011.

[5]辛树轩.p-GaN HEMT器件高温偏置可靠性研究[D].东南大学,2022.DOI:10.27014/d.cnki.gdnau.2022.004027.

[6] E. R. Heller, "Simulation of Life Testing Procedures for Estimating Long-Term Degradation and Lifetime of AlGaN/GaN HEMTs," in IEEE Transactions on Electron Devices, vol. 55, no. 10, pp. 2554-2560, Oct. 2008, doi: 10.1109/TED.2008.2003220.