大学物理复习6->刚体运动学（转动定律+转动惯量）
A.角度（位移）、角速度（速度）、角加速度（加速度）的关系式↓：
B.刚体定轴转动例题实战↓：
A.力矩部分（分成两种情况：力在转动平面内；力在转动平面之外）
a.力在转动平面内（示意图见下↓）：只需要进行一次分解
注：需要将力在平面内分解成与位置矢量平行和垂直的方向，只有垂直的方向才有力矩
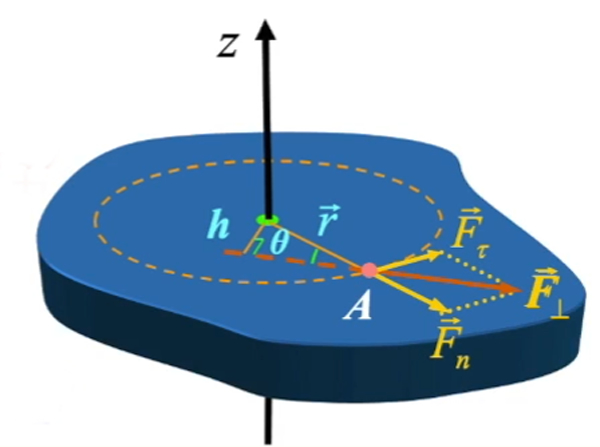
b.力在空间中（示意图见下↓）需要进行两次分解
注：需要先将力分解成与转动轴垂直和平行两个方向的分力，平行的力没有转动效果（相当于在门底抬门，或者在门上压门，起不到开门的效果），垂直的力才有转动的效果（垂直的力在转动平面内，相当于把情况转化成了a情况）再根据a情况分解即可
c.两种情况的推导分析↓：
B.角动量部分（具体推导见下图↓）
C.转动惯量（由角动量部分推导而来↓）
a.转动惯量的表达式↓
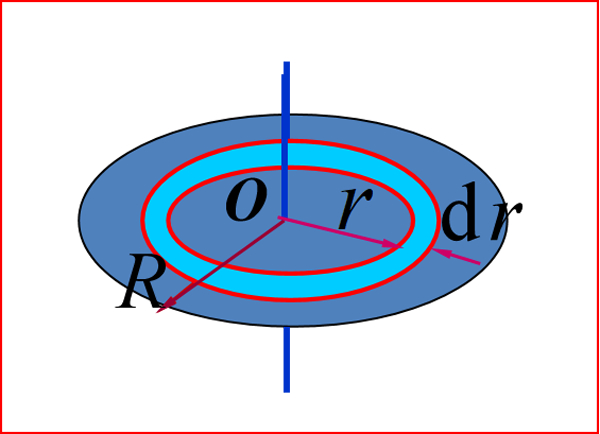
b.求解各种几何体的转动惯量**（解题步骤：先列出元转动惯量的表达式dj，再利用线密度面密度等参数表达dm的微分，最后等式两边同时进行积分即可）**
①圆环的转动惯量↓
②圆盘的转动惯量↓
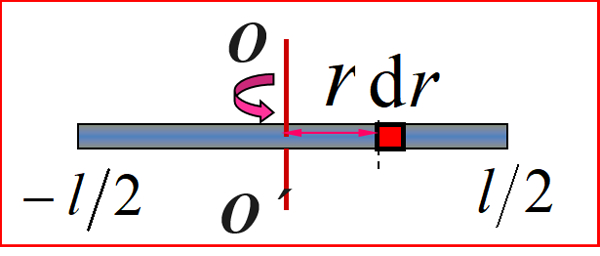
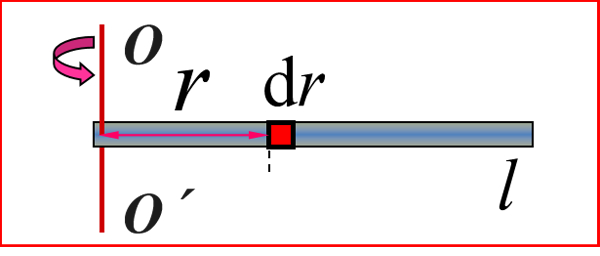
③细棒的转动惯量↓（前者为轴在中间的转动惯量，后者为轴在左侧的转动惯量）
D.转动定律的实际应用（与求转动惯量一样，都是表达出元物理量，转换微元的形式，再积分求解）
扫一扫
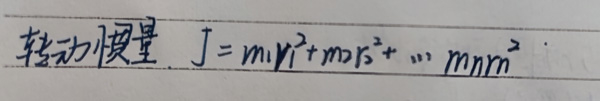
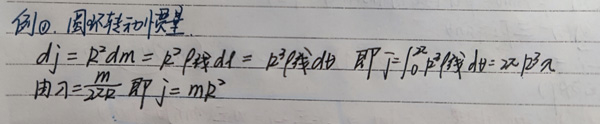
5万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
