前言
刚体运动旋转一般用:欧拉角、四元数、轴角对等表示,在对某个坐标旋转的时候,只需将欧拉角或四元数转换为旋转矩阵,并与原始坐标相乘,便可得到旋转以后的坐标。这里主要看看欧拉角、四元数和旋转矩阵。
国际惯例,参考博客:
欧拉角
静态定义:
描述定点转动刚体的位形需要三个独立坐标变量。描述定轴转动刚体的位形需要一个独立坐标变量,即转角。将定点运动的过程分解为三个相互独立的转角即欧拉角,由章动角,旋进角(即进动角)和自转角组成。
欧拉角的基本思想是将角位移分解为绕三个互相垂直轴的三个旋转组成的序列。欧拉角用来描述刚体在三维欧几里得空间的取向。对于三维空间里的一个参考系,任何坐标系的取向,都可以用三个欧拉角来表现。参考系又称为实验室参考系,是静止不动的。而坐标系则固定于刚体,随着刚体的旋转而旋转。
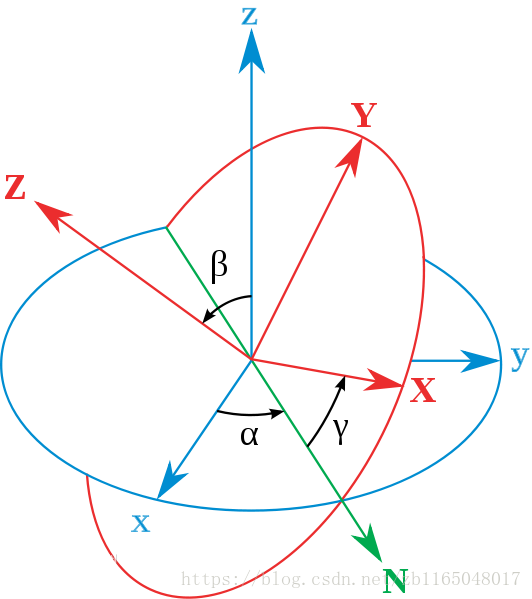
图1. 三个欧拉角 ( α , β , γ ) (\alpha,\beta,\gamma) (α,β,γ),蓝色的轴是xyz轴,红色的轴是XYZ坐标轴,绿色的线是交点线N
对于图1 的一些解释和规范:
- 由定点O做出固定坐标系Oxyz和固定于刚体的动坐标系OXYZ,以轴Oz与OZ为基本轴,以其垂直面Oxy和OXY为基本平面。
- 由Oz转动到OZ的角 β β β称为章动角。平面zOZ的垂线(基本平面Oxy和OXY的交线)ON称为节线。由固定轴x到节线ON的角度 α α α称旋进角;由节线到动轴OX的角 γ γ γ称为自转角
zxz顺规的欧拉角的定义:
- α α α是x-轴与交点线的夹角(0-2π)
- β β β是z轴与Z轴之间的夹角(0-π,因为Z与z的夹角不可能大于180度)
- γ γ γ是交点线与X-轴之间的夹角(0-2π)
对应于每一个取向,设定的一组欧拉角都是独特唯一的,除了某些例外:
- 两组欧拉角 α α α,一个是0,一个是2π,而β和γ分别相等,则此两组欧拉角都描述同样的取向。
- 两组欧拉角 γ γ γ,一个是0,一个是2π,而α与β分别相等,则此两组欧拉角都描述同样的取向。
动态定义:
有两种不同的动态定义。一种是绕着固定于刚体的坐标轴的三个旋转的复合。另一种是绕着实验室参考轴的三个旋转复合。注意XYZ坐标轴是旋转的刚体坐标轴,而xyz坐标轴是静止不动的实验室参考轴。
A) 绕着XYZ坐标轴旋转:最初,两个坐标系统xyz和XYZ的坐标轴都是重叠着的,开始绕着Z轴旋转 α α α角度,然后绕着X旋转 β β β角度,再绕Z轴旋转 γ γ γ角度。
B) 绕着xyz坐标轴旋转:最初,两个坐标系统xyz和XYZ的坐标轴都是重叠着的,开始绕着z轴旋转 γ γ γ角度,然后绕着x旋转 α α α角度,最后绕着z轴旋转 β β β。
万向锁
欧拉角的一个相关概念:万向节死锁(Gimbal Lock)简称万向节锁或者万向锁
产生原因是:三个万向节其中两个的轴发生重合,会失去一个自由度的情形。
导致的后果:由于万向锁的存在,欧拉角无法实现球面平滑插值。解决方法是使用四元数球面线性插值。
其它
三个欧拉角是相互独立变化的,改变其中任一个不改变其它两个。确定了三个欧拉角在任意时刻的大小,也就确定了刚体在任意时刻的位形。
欧拉角描述的常用来描述物体相对于父坐标空间方位的方法。基本思想是将角位移分解为绕三个相互垂直轴的三个旋转组成的序列。对于三维空间中的一个坐标系,任何坐标系的去向都可以用三个欧拉角来表现,其中参考坐标系是静止不动的,又称为实验室坐标系。
xzx顺规的方法:初始坐标系XYZ可看做与参考坐标系xyz重合,之后先绕z轴旋转φ角度值,再绕x轴旋转θ角度值,最后绕z轴旋转ψ角度值。
ASF文件中有明确规定,应该都是zyx顺规方向。
欧拉角仅用三个角度值就可以表示方位信息,并且这三个数值的范围都是 ( 0 , 2 π ) (0,2π) (0,2π)任取的。这两个特征是欧拉角独有的。
然而欧拉角两个致命缺点是:
- 对于一个给定的方位存在多个欧拉角与之对应,称为“别名问题”
- 由于欧拉角顺规的规定,欧拉角 的旋转一定要按照某个特定次序进行。等量的欧拉角变化可能引起完全不同的旋转变化结构。并且欧拉角可能导致自由度丧失,造成旋转不平衡问题,从而造成“万向锁”现象,导致抖动、路径错误等现象。
欧拉动力学方程
角速度与欧拉角之间的关系推导:设三个欧拉角分别为旋进角(进动角) φ,章动角θ,自转角ψ。
在任意时刻角速度可分解为如下三个定轴转动角速度之和:
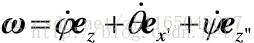


四元数
定义:
四元数都是 1 、 i 、 j 、 k 1、i、j、k 1、i、j、k的线性组合,一般可表示为
d + a i + b j + c k ( i ∗ i = j ∗ j = k ∗ k = − 1 , i j = k 、 j i = − k 、 j k = i 、 k j = − i 、 k i = j 、 i k = − j ) d+ai+bj+ck(i*i=j*j=k*k=-1,ij=k、ji=-k、jk=i、kj=-i、ki=j、ik=-j) d+ai+bj+ck(i∗i=j∗j=k∗k=−1,ij=k、ji=−k、jk=i、kj=−i、ki=j、ik=−j)
a , b , c , d a,b,c,d a,b,c,d都是实数。如把四元数的集合考虑成多维实数空间的话,四元数就代表着一个四维空间,相对于复数为二维空间。
对于 i , j , k i,j,k i,j,k本身的几何意义可以理解为一种旋转,其中 i i i旋转代表X轴与Y轴相交平面中X轴正向向Y轴正向的旋转。 j j j旋转代表Z轴与X轴相交平面中Z轴正向向X轴正向的旋转。 k k k旋转代表Y轴与Z轴相交平面中Y轴正向向Z轴正向的旋转。
加乘运算:
两个四元数: p = d + a i + b j + c k , q = w + x i + y j + z k p=d+ai+bj+ck,q=w+xi+yj+zk p=d+ai+bj+ck,q=w+xi+yj+zk
加法: p + q = ( d + w ) + ( a + x ) i + ( b + y ) j + ( c + z ) k p+q=(d+w)+(a+x)i+(b+y)j+(c+z)k p+q=(d+w)+(a+x)i+(b+y)j+(c+z)k
乘法:
p
⋅
q
=
(
d
+
a
i
+
b
j
+
c
k
)
(
w
+
x
i
+
y
j
+
z
k
)
=
(
d
w
−
a
x
−
b
y
−
c
z
)
+
(
a
w
+
d
x
+
b
z
−
c
y
)
i
+
(
b
w
+
d
y
+
c
x
−
a
z
)
j
+
(
c
w
+
d
z
+
a
y
−
b
x
)
k
\begin{aligned} p\cdot q&=(d+ai+bj+ck)(w+xi+yj+zk)\\ &=(dw-ax-by-cz)+(aw+dx+bz-cy)i\\ &\quad +(bw+dy+cx-az)j+(cw+dz+ay-bx)k \end{aligned}
p⋅q=(d+ai+bj+ck)(w+xi+yj+zk)=(dw−ax−by−cz)+(aw+dx+bz−cy)i+(bw+dy+cx−az)j+(cw+dz+ay−bx)k
四元数也可以描述为
q
=
[
w
,
v
]
q=[w,v]
q=[w,v],其中
V
=
(
x
,
y
,
z
)
V=(x,y,z)
V=(x,y,z)是矢量,
w
w
w是标量
我们通常称这两个部分是四元数的实数部分和(三维)向量部分,那么两个四元数的乘积就可以表示为
p
⋅
q
=
(
d
+
u
)
(
w
+
v
)
=
d
w
−
<
u
,
v
>
+
d
v
+
w
u
+
u
×
v
p\cdot q=(d+u)(w+v)=dw-<u,v>+dv+wu+u\times v
p⋅q=(d+u)(w+v)=dw−<u,v>+dv+wu+u×v
如果交换乘积
q
⋅
p
=
w
d
−
<
v
,
u
>
+
w
u
+
d
v
+
v
×
u
q\cdot p=wd-<v,u>+wu+dv+v\times u
q⋅p=wd−<v,u>+wu+dv+v×u
如果向量部分外积为零,那么四元数的乘积就可以互换了
四元数的优点:
四元数表达式无奇点,角度计算的工作量较少,使误差减小,结果更加准确,其次能够避免“万向锁”问题,在插值方面有极大的优越性。最后,单位四元数可以表示三维空间中的一个转动。
轴角对
提供一个旋转轴以及绕此轴旋转的角度,可以转换为四元数:
w
=
cos
(
α
2
)
x
=
sin
(
α
2
)
cos
(
β
x
)
y
=
sin
(
α
2
)
cos
(
β
y
)
z
=
sin
(
α
2
)
cos
(
β
z
)
\begin{aligned} w&=\cos (\frac{\alpha}{2})\\ x&=\sin (\frac{\alpha}{2})\cos (\beta_x)\\ y&=\sin (\frac{\alpha}{2})\cos (\beta_y)\\ z&=\sin (\frac{\alpha}{2})\cos (\beta_z) \end{aligned}
wxyz=cos(2α)=sin(2α)cos(βx)=sin(2α)cos(βy)=sin(2α)cos(βz)
其中
α
\alpha
α是绕旋转轴旋转的角度,
cos
(
β
x
)
,
cos
(
β
y
)
,
cos
(
β
z
)
\cos(\beta_x),\cos(\beta_y),\cos(\beta_z)
cos(βx),cos(βy),cos(βz)是旋转轴在xyz方向的分量
旋转矩阵
三维空间中的旋转变化比二维的复杂。需要指定旋转角和旋转轴。若以坐标系的三个坐标轴xyz作为旋转轴,则点实际只是在垂直坐标轴的平面上做二维变换,可以用二维公式推出三维变换矩阵。规定,右手坐标系中,旋转正方向是右手螺旋方向,即从该轴正半轴向原点看是逆时针方向。
绕z轴旋转:
(
x
′
,
y
′
,
z
′
)
=
(
x
,
y
,
z
,
1
)
[
cos
γ
sin
γ
0
0
−
sin
γ
cos
γ
0
0
0
0
1
0
0
0
0
1
]
(x',y',z')=(x,y,z,1)\begin{bmatrix} \cos \gamma&\sin \gamma & 0&0\\ -\sin\gamma&\cos \gamma &0&0\\ 0&0&1&0\\ 0&0&0&1 \end{bmatrix}
(x′,y′,z′)=(x,y,z,1)⎣⎢⎢⎡cosγ−sinγ00sinγcosγ0000100001⎦⎥⎥⎤
绕x轴旋转:
(
x
′
,
y
′
,
z
′
)
=
(
x
,
y
,
z
,
1
)
[
1
0
0
0
0
cos
α
sin
α
0
0
−
sin
α
cos
α
0
0
0
0
1
]
(x',y',z')=(x,y,z,1)\begin{bmatrix} 1&0&0&0\\ 0&\cos \alpha&\sin\alpha&0\\ 0&-\sin \alpha&\cos \alpha&0\\ 0&0&0&1 \end{bmatrix}
(x′,y′,z′)=(x,y,z,1)⎣⎢⎢⎡10000cosα−sinα00sinαcosα00001⎦⎥⎥⎤
绕y轴旋转:
(
x
′
,
y
′
,
z
′
)
=
(
x
,
y
,
z
,
1
)
[
cos
β
0
−
sin
β
0
0
1
0
0
sin
β
0
cos
β
0
0
0
0
1
]
(x',y',z')=(x,y,z,1)\begin{bmatrix} \cos\beta&0&-\sin\beta&0\\ 0&1&0&0\\ \sin\beta&0&\cos\beta&0\\ 0&0&0&1 \end{bmatrix}
(x′,y′,z′)=(x,y,z,1)⎣⎢⎢⎡cosβ0sinβ00100−sinβ0cosβ00001⎦⎥⎥⎤
绕任意轴旋转公式(
(
a
,
b
,
c
)
(a,b,c)
(a,b,c)表示旋转轴,
θ
\theta
θ表示旋转角度):
[
a
2
+
(
1
−
a
2
)
cos
θ
a
b
(
1
−
cos
θ
+
c
sin
θ
a
c
(
1
−
cos
θ
)
−
b
sin
θ
0
a
b
(
1
−
cos
θ
)
−
c
sin
θ
b
2
+
(
1
−
b
2
)
cos
θ
b
c
(
1
−
cos
θ
)
+
a
sin
θ
0
a
c
(
1
−
cos
θ
)
+
b
sin
θ
b
c
(
1
−
cos
θ
)
−
a
sin
θ
c
2
+
(
1
−
c
2
)
cos
θ
0
0
0
0
1
]
\begin{bmatrix} a^2+(1-a^2)\cos\theta&ab(1-\cos\theta+c\sin\theta&ac(1-\cos\theta)-b\sin\theta&0\\ ab(1-\cos\theta)-c\sin\theta&b^2+(1-b^2)\cos\theta&bc(1-\cos\theta)+a\sin\theta&0\\ ac(1-\cos\theta)+b\sin\theta&bc(1-\cos\theta)-a\sin\theta&c^2+(1-c^2)\cos\theta&0\\ 0&0&0&1 \end{bmatrix}
⎣⎢⎢⎡a2+(1−a2)cosθab(1−cosθ)−csinθac(1−cosθ)+bsinθ0ab(1−cosθ+csinθb2+(1−b2)cosθbc(1−cosθ)−asinθ0ac(1−cosθ)−bsinθbc(1−cosθ)+asinθc2+(1−c2)cosθ00001⎦⎥⎥⎤
互相转换
欧拉角到四元数的转换
q
=
[
w
x
y
z
]
=
[
cos
(
φ
2
)
cos
(
θ
2
)
cos
(
ψ
2
)
+
sin
(
φ
2
)
sin
(
θ
2
)
sin
(
ψ
2
)
sin
(
φ
2
)
cos
(
θ
2
)
cos
(
ψ
2
)
−
cos
(
φ
2
)
sin
(
θ
2
)
sin
(
ψ
2
)
cos
(
φ
2
)
sin
(
θ
2
)
cos
(
ψ
2
)
+
sin
(
φ
2
)
cos
(
θ
2
)
sin
(
ψ
2
)
cos
(
φ
2
)
cos
(
θ
2
)
sin
(
ψ
2
)
−
sin
(
φ
2
)
sin
(
θ
2
)
cos
(
ψ
2
)
]
q=\begin{bmatrix} w\\x\\y\\z \end{bmatrix}=\begin{bmatrix} \cos(\frac{\varphi}{2})\cos(\frac{\theta}{2})\cos(\frac{\psi}{2})+\sin(\frac{\varphi}{2})\sin(\frac{\theta}{2})\sin(\frac{\psi}{2})\\ \sin(\frac{\varphi}{2})\cos(\frac{\theta}{2})\cos(\frac{\psi}{2})-\cos(\frac{\varphi}{2})\sin(\frac{\theta}{2})\sin(\frac{\psi}{2})\\ \cos(\frac{\varphi}{2})\sin(\frac{\theta}{2})\cos(\frac{\psi}{2})+\sin(\frac{\varphi}{2})\cos(\frac{\theta}{2})\sin(\frac{\psi}{2})\\ \cos(\frac{\varphi}{2})\cos(\frac{\theta}{2})\sin(\frac{\psi}{2})-\sin(\frac{\varphi}{2})\sin(\frac{\theta}{2})\cos(\frac{\psi}{2}) \end{bmatrix}
q=⎣⎢⎢⎡wxyz⎦⎥⎥⎤=⎣⎢⎢⎡cos(2φ)cos(2θ)cos(2ψ)+sin(2φ)sin(2θ)sin(2ψ)sin(2φ)cos(2θ)cos(2ψ)−cos(2φ)sin(2θ)sin(2ψ)cos(2φ)sin(2θ)cos(2ψ)+sin(2φ)cos(2θ)sin(2ψ)cos(2φ)cos(2θ)sin(2ψ)−sin(2φ)sin(2θ)cos(2ψ)⎦⎥⎥⎤
四元数到欧拉角的转换
[
φ
θ
ψ
]
=
[
arctan
2
(
w
x
+
y
z
)
1
−
2
(
x
2
+
y
2
)
arcsin
(
2
(
w
y
−
z
x
)
)
arctan
(
2
(
w
z
+
x
y
)
1
−
2
(
y
2
+
z
2
)
)
]
\begin{bmatrix} \varphi\\\theta\\\psi \end{bmatrix}=\begin{bmatrix} \arctan \frac{2(wx+yz)}{1-2(x^2+y^2)}\\ \arcsin(2(wy-zx))\\ \arctan(\frac{2(wz+xy)}{1-2(y^2+z^2)}) \end{bmatrix}
⎣⎡φθψ⎦⎤=⎣⎢⎡arctan1−2(x2+y2)2(wx+yz)arcsin(2(wy−zx))arctan(1−2(y2+z2)2(wz+xy))⎦⎥⎤
arctan和arcsin的结果是
[
−
π
2
,
π
2
]
[-\frac{\pi}{2},\frac{\pi}{2}]
[−2π,2π],这无法覆盖所有的朝向(对于
θ
\theta
θ角
[
−
π
2
,
π
2
]
[-\frac{\pi}{2},\frac{\pi}{2}]
[−2π,2π]已经满足),因此需要atan2代替arctan
[
φ
θ
ψ
]
=
[
a
t
a
n
2
(
2
(
w
x
+
y
z
)
,
1
−
2
(
x
2
+
y
2
)
)
arcsin
(
2
(
w
y
−
z
x
)
)
a
t
a
n
2
(
2
(
w
z
+
x
y
)
,
1
−
2
(
y
2
+
z
2
)
)
]
\begin{bmatrix} \varphi\\\theta\\\psi \end{bmatrix}=\begin{bmatrix} atan2(2(wx+yz),1-2(x^2+y^2))\\ \arcsin(2(wy-zx))\\ atan2(2(wz+xy),1-2(y^2+z^2)) \end{bmatrix}
⎣⎡φθψ⎦⎤=⎣⎡atan2(2(wx+yz),1−2(x2+y2))arcsin(2(wy−zx))atan2(2(wz+xy),1−2(y2+z2))⎦⎤
【注】*atan2(y,x)*表达的意思是坐标原点为起点,指向
(
x
,
y
)
(x,y)
(x,y)的射线在坐标平面上与
x
x
x轴正方向之间的角度
旋转矩阵,欧拉角,四元数比较
旋转矩阵,欧拉角,四元数主要用于:向量的旋转、坐标系之间的转换、角位移的计算、方位的平滑插值计算。
不同的方位表示方法适用于不同的情况:
- 欧拉角最容易使用。当需要为世界中的物体指定方位时,欧拉角能大大简化人机交互,包括直接键盘输入方位、在代码中指定方位(如为渲染设定摄像机)、在调试中测试。
- 如果需要在坐标系之间转换向量,就选择矩阵形式。另一种方法是用欧拉角作为方位的“主拷贝“,但同时维护一个旋转矩阵,当欧拉角发生改变时,矩阵也要同时进行更新。
- 当需要大量保存方位数据(如动画)时,就使用欧拉角或者四元数,欧拉角少占用25%内存,但是转换到矩阵慢。如果动画数据需要嵌套坐标系之间的连接,四元数可能是最好的选择。
- 平滑插值只能用四元数。用其它形式则必须转到四元数,插值完毕再转回去。
| 任务/性质 | 旋转矩阵 | 欧拉角 | 四元数 |
|---|---|---|---|
| 在坐标系间(物体和惯性)旋转点 | 能 | 不能(必须转换到矩阵) | 不能(必须转换到矩阵) |
| 连接或增量旋转 | 能,但是经常比四元数慢,小心矩阵蠕变的情况 | 不能 | 能,比矩阵快 |
| 插值 | 基本不能 | 能,但是容易遇到万向锁或者其他问题 | Slerp提供了平滑插值 |
| 易用程度 | 难 | 易 | 难 |
| 在内存或文件中存储 | 9个数 | 3个数 | 4个数 |
| 对给定方位的表达式是否唯一 | 是 | 不是,对同一方位有无数多中方法 | 不是,有两种方法,它们互相为互 |
| 可能导致非法 | 矩阵蠕变 | 任意三个数都能构成合法的欧拉角 | 容易产生误差积累,从而产生非法的四元数 |
matlab自带函数
**angle2quat.m **
function q = angle2quat( r1, r2, r3, varargin )
% ANGLE2QUAT Convert rotation angles to quaternion.
% Q = ANGLE2QUAT( R1, R2, R3 ) calculates the quaternion, Q, for given,
% R1, R2, R3. R1 is an M array of first rotation angles. R2 is an M
% array of second rotation angles. R3 is an M array of third rotation
% angles. Q returns an M-by-4 matrix containing M quaternions. Q has its
% scalar number as the first column. Rotation angles are input in radians.
%
% Q = ANGLE2QUAT( R1, R2, R3, S ) calculates the quaternion, Q, for a
% given set of rotation angles, R1, R2, R3, and a specified rotation
% sequence, S.
%
% The default rotation sequence is 'ZYX' where the order of rotation
% angles for the default rotation are R1 = Z Axis Rotation, R2 = Y Axis
% Rotation, and R3 = X Axis Rotation.
%
% All rotation sequences, S, are supported: 'ZYX', 'ZYZ', 'ZXY', 'ZXZ',
% 'YXZ', 'YXY', 'YZX', 'YZY', 'XYZ', 'XYX', 'XZY', and 'XZX'.
%
% Examples:
%
% Determine the quaternion from rotation angles:
% yaw = 0.7854;
% pitch = 0.1;
% roll = 0;
% q = angle2quat( yaw, pitch, roll )
%
% Determine the quaternions from multiple rotation angles:
% yaw = [0.7854 0.5];
% pitch = [0.1 0.3];
% roll = [0 0.1];
% q = angle2quat( pitch, roll, yaw, 'YXZ' )
%
% See also DCM2QUAT, QUAT2DCM, QUAT2ANGLE.
% Copyright 2000-2011 The MathWorks, Inc.
if any(~isreal(r1) || ~isnumeric(r1))
error(message('aero:angle2quat:isNotReal1'));
end
if any(~isreal(r2) || ~isnumeric(r2))
error(message('aero:angle2quat:isNotReal2'));
end
if any(~isreal(r3) || ~isnumeric(r3))
error(message('aero:angle2quat:isNotReal3'));
end
if (length(r1) ~= length(r2)) || (length(r1) ~= length(r3))
error(message('aero:angle2quat:wrongDimension'));
end
if nargin == 3
type = 'zyx';
else
if ischar( varargin{1} )
type = varargin{1};
else
error(message('aero:angle2quat:notChar'));
end
end
angles = [r1(:) r2(:) r3(:)];
cang = cos( angles/2 );
sang = sin( angles/2 );
switch lower( type )
case 'zyx'
q = [ cang(:,1).*cang(:,2).*cang(:,3) + sang(:,1).*sang(:,2).*sang(:,3), ...
cang(:,1).*cang(:,2).*sang(:,3) - sang(:,1).*sang(:,2).*cang(:,3), ...
cang(:,1).*sang(:,2).*cang(:,3) + sang(:,1).*cang(:,2).*sang(:,3), ...
sang(:,1).*cang(:,2).*cang(:,3) - cang(:,1).*sang(:,2).*sang(:,3)];
case 'zyz'
q = [ cang(:,1).*cang(:,2).*cang(:,3) - sang(:,1).*cang(:,2).*sang(:,3), ...
cang(:,1).*sang(:,2).*sang(:,3) - sang(:,1).*sang(:,2).*cang(:,3), ...
cang(:,1).*sang(:,2).*cang(:,3) + sang(:,1).*sang(:,2).*sang(:,3), ...
sang(:,1).*cang(:,2).*cang(:,3) + cang(:,1).*cang(:,2).*sang(:,3)];
case 'zxy'
q = [ cang(:,1).*cang(:,2).*cang(:,3) - sang(:,1).*sang(:,2).*sang(:,3), ...
cang(:,1).*sang(:,2).*cang(:,3) - sang(:,1).*cang(:,2).*sang(:,3), ...
cang(:,1).*cang(:,2).*sang(:,3) + sang(:,1).*sang(:,2).*cang(:,3), ...
cang(:,1).*sang(:,2).*sang(:,3) + sang(:,1).*cang(:,2).*cang(:,3)];
case 'zxz'
q = [ cang(:,1).*cang(:,2).*cang(:,3) - sang(:,1).*cang(:,2).*sang(:,3), ...
cang(:,1).*sang(:,2).*cang(:,3) + sang(:,1).*sang(:,2).*sang(:,3), ...
sang(:,1).*sang(:,2).*cang(:,3) - cang(:,1).*sang(:,2).*sang(:,3), ...
cang(:,1).*cang(:,2).*sang(:,3) + sang(:,1).*cang(:,2).*cang(:,3)];
case 'yxz'
q = [ cang(:,1).*cang(:,2).*cang(:,3) + sang(:,1).*sang(:,2).*sang(:,3), ...
cang(:,1).*sang(:,2).*cang(:,3) + sang(:,1).*cang(:,2).*sang(:,3), ...
sang(:,1).*cang(:,2).*cang(:,3) - cang(:,1).*sang(:,2).*sang(:,3), ...
cang(:,1).*cang(:,2).*sang(:,3) - sang(:,1).*sang(:,2).*cang(:,3)];
case 'yxy'
q = [ cang(:,1).*cang(:,2).*cang(:,3) - sang(:,1).*cang(:,2).*sang(:,3), ...
cang(:,1).*sang(:,2).*cang(:,3) + sang(:,1).*sang(:,2).*sang(:,3), ...
sang(:,1).*cang(:,2).*cang(:,3) + cang(:,1).*cang(:,2).*sang(:,3), ...
cang(:,1).*sang(:,2).*sang(:,3) - sang(:,1).*sang(:,2).*cang(:,3)];
case 'yzx'
q = [ cang(:,1).*cang(:,2).*cang(:,3) - sang(:,1).*sang(:,2).*sang(:,3), ...
cang(:,1).*cang(:,2).*sang(:,3) + sang(:,1).*sang(:,2).*cang(:,3), ...
cang(:,1).*sang(:,2).*sang(:,3) + sang(:,1).*cang(:,2).*cang(:,3), ...
cang(:,1).*sang(:,2).*cang(:,3) - sang(:,1).*cang(:,2).*sang(:,3)];
case 'yzy'
q = [ cang(:,1).*cang(:,2).*cang(:,3) - sang(:,1).*cang(:,2).*sang(:,3), ...
sang(:,1).*sang(:,2).*cang(:,3) - cang(:,1).*sang(:,2).*sang(:,3), ...
cang(:,1).*cang(:,2).*sang(:,3) + sang(:,1).*cang(:,2).*cang(:,3), ...
cang(:,1).*sang(:,2).*cang(:,3) + sang(:,1).*sang(:,2).*sang(:,3)];
case 'xyz'
q = [ cang(:,1).*cang(:,2).*cang(:,3) - sang(:,1).*sang(:,2).*sang(:,3), ...
cang(:,1).*sang(:,2).*sang(:,3) + sang(:,1).*cang(:,2).*cang(:,3), ...
cang(:,1).*sang(:,2).*cang(:,3) - sang(:,1).*cang(:,2).*sang(:,3), ...
cang(:,1).*cang(:,2).*sang(:,3) + sang(:,1).*sang(:,2).*cang(:,3)];
case 'xyx'
q = [ cang(:,1).*cang(:,2).*cang(:,3) - sang(:,1).*cang(:,2).*sang(:,3), ...
cang(:,1).*cang(:,2).*sang(:,3) + sang(:,1).*cang(:,2).*cang(:,3), ...
cang(:,1).*sang(:,2).*cang(:,3) + sang(:,1).*sang(:,2).*sang(:,3), ...
sang(:,1).*sang(:,2).*cang(:,3) - cang(:,1).*sang(:,2).*sang(:,3)];
case 'xzy'
q = [ cang(:,1).*cang(:,2).*cang(:,3) + sang(:,1).*sang(:,2).*sang(:,3), ...
sang(:,1).*cang(:,2).*cang(:,3) - cang(:,1).*sang(:,2).*sang(:,3), ...
cang(:,1).*cang(:,2).*sang(:,3) - sang(:,1).*sang(:,2).*cang(:,3), ...
cang(:,1).*sang(:,2).*cang(:,3) + sang(:,1).*cang(:,2).*sang(:,3)];
case 'xzx'
q = [ cang(:,1).*cang(:,2).*cang(:,3) - sang(:,1).*cang(:,2).*sang(:,3), ...
cang(:,1).*cang(:,2).*sang(:,3) + sang(:,1).*cang(:,2).*cang(:,3), ...
cang(:,1).*sang(:,2).*sang(:,3) - sang(:,1).*sang(:,2).*cang(:,3), ...
cang(:,1).*sang(:,2).*cang(:,3) + sang(:,1).*sang(:,2).*sang(:,3)];
otherwise
error(message('aero:angle2quat:unknownRotation', type));
end
**quat2angle.m **
function [r1, r2, r3] = quat2angle( q, varargin )
% QUAT2ANGLE Convert quaternion to rotation angles.
% [R1 R2 R3] = QUAT2ANGLE( Q ) calculates the calculates the set of
% rotation angles, R1, R2, R3, for a given quaternion, Q. Input Q is an
% M-by-4 matrix containing M quaternions. R1 returns an M array of
% first rotation angles. R2 returns an M array of second rotation
% angles. R3 returns an M array of third rotation angles. Each element
% of Q must be a real number. Additionally, Q has its scalar number as
% the first column. Rotation angles are output in radians.
%
% [R1 R2 R3] = QUAT2ANGLE( Q, S ) calculates the set of rotation
% angles, R1, R2, R3, for a given quaternion, Q, and a
% specified rotation sequence, S.
%
% The default rotation sequence is 'ZYX' where the order of rotation
% angles for the default rotation are R1 = Z Axis Rotation, R2 = Y Axis
% Rotation, and R3 = X Axis Rotation.
%
% All rotation sequences, S, are supported: 'ZYX', 'ZYZ', 'ZXY', 'ZXZ',
% 'YXZ', 'YXY', 'YZX', 'YZY', 'XYZ', 'XYX', 'XZY', and 'XZX'.
%
% Examples:
%
% Determine the rotation angles from q = [1 0 1 0]:
% [yaw, pitch, roll] = quat2angle([1 0 1 0])
%
% Determine the rotation angles from multiple quaternions:
% q = [1 0 1 0; 1 0.5 0.3 0.1];
% [pitch, roll, yaw] = quat2angle(q, 'YXZ')
%
% See also ANGLE2DCM, DCM2ANGLE, DCM2QUAT, ANGLE2QUAT, QUAT2DCM.
% Copyright 2000-2007 The MathWorks, Inc.
% $Revision: 1.1.6.1 $ $Date: 2007/05/10 13:42:36 $
% Limitations:
% The limitations for the 'ZYX', 'ZXY', 'YXZ', 'YZX', 'XYZ', and 'XZY'
% implementations generate an R2 angle that lies between +/- 90
% degrees, and R1 and R3 angles that lie between +/- 180 degrees.
%
% The limitations for the 'ZYZ', 'ZXZ', 'YXY', 'YZY', 'XYX', and 'XZX'
% implementations generate an R2 angle that lies between 0 and
% 180 degrees, and R1 and R3 angles that lie between +/- 180 degrees.
% error(nargchk(1, 2, nargin,'struct'));
if nargin == 1
type = 'zyx';
else
if ischar( varargin{1} )
type = varargin{1};
else
error('aero:quat2angle:notchar','Rotation sequence is not a string.');
end
end
qin = quatnormalize( q );
switch lower( type )
case 'zyx'
[r1, r2, r3] = threeaxisrot( 2.*(qin(:,2).*qin(:,3) + qin(:,1).*qin(:,4)), ...
qin(:,1).^2 + qin(:,2).^2 - qin(:,3).^2 - qin(:,4).^2, ...
-2.*(qin(:,2).*qin(:,4) - qin(:,1).*qin(:,3)), ...
2.*(qin(:,3).*qin(:,4) + qin(:,1).*qin(:,2)), ...
qin(:,1).^2 - qin(:,2).^2 - qin(:,3).^2 + qin(:,4).^2);
case 'zyz'
[r1, r2, r3] = twoaxisrot( 2.*(qin(:,3).*qin(:,4) - qin(:,1).*qin(:,2)), ...
2.*(qin(:,2).*qin(:,4) + qin(:,1).*qin(:,3)), ...
qin(:,1).^2 - qin(:,2).^2 - qin(:,3).^2 + qin(:,4).^2, ...
2.*(qin(:,3).*qin(:,4) + qin(:,1).*qin(:,2)), ...
-2.*(qin(:,2).*qin(:,4) - qin(:,1).*qin(:,3)));
case 'zxy'
[r1, r2, r3] = threeaxisrot( -2.*(qin(:,2).*qin(:,3) - qin(:,1).*qin(:,4)), ...
qin(:,1).^2 - qin(:,2).^2 + qin(:,3).^2 - qin(:,4).^2, ...
2.*(qin(:,3).*qin(:,4) + qin(:,1).*qin(:,2)), ...
-2.*(qin(:,2).*qin(:,4) - qin(:,1).*qin(:,3)), ...
qin(:,1).^2 - qin(:,2).^2 - qin(:,3).^2 + qin(:,4).^2);
case 'zxz'
[r1, r2, r3] = twoaxisrot( 2.*(qin(:,2).*qin(:,4) + qin(:,1).*qin(:,3)), ...
-2.*(qin(:,3).*qin(:,4) - qin(:,1).*qin(:,2)), ...
qin(:,1).^2 - qin(:,2).^2 - qin(:,3).^2 + qin(:,4).^2, ...
2.*(qin(:,2).*qin(:,4) - qin(:,1).*qin(:,3)), ...
2.*(qin(:,3).*qin(:,4) + qin(:,1).*qin(:,2)));
case 'yxz'
[r1, r2, r3] = threeaxisrot( 2.*(qin(:,2).*qin(:,4) + qin(:,1).*qin(:,3)), ...
qin(:,1).^2 - qin(:,2).^2 - qin(:,3).^2 + qin(:,4).^2, ...
-2.*(qin(:,3).*qin(:,4) - qin(:,1).*qin(:,2)), ...
2.*(qin(:,2).*qin(:,3) + qin(:,1).*qin(:,4)), ...
qin(:,1).^2 - qin(:,2).^2 + qin(:,3).^2 - qin(:,4).^2);
case 'yxy'
[r1, r2, r3] = twoaxisrot( 2.*(qin(:,2).*qin(:,3) - qin(:,1).*qin(:,4)), ...
2.*(qin(:,3).*qin(:,4) + qin(:,1).*qin(:,2)), ...
qin(:,1).^2 - qin(:,2).^2 + qin(:,3).^2 - qin(:,4).^2, ...
2.*(qin(:,2).*qin(:,3) + qin(:,1).*qin(:,4)), ...
-2.*(qin(:,3).*qin(:,4) - qin(:,1).*qin(:,2)));
case 'yzx'
[r1, r2, r3] = threeaxisrot( -2.*(qin(:,2).*qin(:,4) - qin(:,1).*qin(:,3)), ...
qin(:,1).^2 + qin(:,2).^2 - qin(:,3).^2 - qin(:,4).^2, ...
2.*(qin(:,2).*qin(:,3) + qin(:,1).*qin(:,4)), ...
-2.*(qin(:,3).*qin(:,4) - qin(:,1).*qin(:,2)), ...
qin(:,1).^2 - qin(:,2).^2 + qin(:,3).^2 - qin(:,4).^2);
case 'yzy'
[r1, r2, r3] = twoaxisrot( 2.*(qin(:,3).*qin(:,4) + qin(:,1).*qin(:,2)), ...
-2.*(qin(:,2).*qin(:,3) - qin(:,1).*qin(:,4)), ...
qin(:,1).^2 - qin(:,2).^2 + qin(:,3).^2 - qin(:,4).^2, ...
2.*(qin(:,3).*qin(:,4) - qin(:,1).*qin(:,2)), ...
2.*(qin(:,2).*qin(:,3) + qin(:,1).*qin(:,4)));
case 'xyz'
[r1, r2, r3] = threeaxisrot( -2.*(qin(:,3).*qin(:,4) - qin(:,1).*qin(:,2)), ...
qin(:,1).^2 - qin(:,2).^2 - qin(:,3).^2 + qin(:,4).^2, ...
2.*(qin(:,2).*qin(:,4) + qin(:,1).*qin(:,3)), ...
-2.*(qin(:,2).*qin(:,3) - qin(:,1).*qin(:,4)), ...
qin(:,1).^2 + qin(:,2).^2 - qin(:,3).^2 - qin(:,4).^2);
case 'xyx'
[r1, r2, r3] = twoaxisrot( 2.*(qin(:,2).*qin(:,3) + qin(:,1).*qin(:,4)), ...
-2.*(qin(:,2).*qin(:,4) - qin(:,1).*qin(:,3)), ...
qin(:,1).^2 + qin(:,2).^2 - qin(:,3).^2 - qin(:,4).^2, ...
2.*(qin(:,2).*qin(:,3) - qin(:,1).*qin(:,4)), ...
2.*(qin(:,2).*qin(:,4) + qin(:,1).*qin(:,3)));
case 'xzy'
[r1, r2, r3] = threeaxisrot( 2.*(qin(:,3).*qin(:,4) + qin(:,1).*qin(:,2)), ...
qin(:,1).^2 - qin(:,2).^2 + qin(:,3).^2 - qin(:,4).^2, ...
-2.*(qin(:,2).*qin(:,3) - qin(:,1).*qin(:,4)), ...
2.*(qin(:,2).*qin(:,4) + qin(:,1).*qin(:,3)), ...
qin(:,1).^2 + qin(:,2).^2 - qin(:,3).^2 - qin(:,4).^2);
case 'xzx'
[r1, r2, r3] = twoaxisrot( 2.*(qin(:,2).*qin(:,4) - qin(:,1).*qin(:,3)), ...
2.*(qin(:,2).*qin(:,3) + qin(:,1).*qin(:,4)), ...
qin(:,1).^2 + qin(:,2).^2 - qin(:,3).^2 - qin(:,4).^2, ...
2.*(qin(:,2).*qin(:,4) + qin(:,1).*qin(:,3)), ...
-2.*(qin(:,2).*qin(:,3) - qin(:,1).*qin(:,4)));
otherwise
error('aero:quat2angle:unknownrotation','Unknown rotation sequence, %s', type);
end
function [r1, r2, r3] = threeaxisrot(r11, r12, r21, r31, r32)
% find angles for rotations about X, Y, and Z axes
r1 = atan2( r11, r12 );
r2 = asin( r21 );
r3 = atan2( r31, r32 );
function [r1, r2, r3] = twoaxisrot(r11, r12, r21, r31, r32)
r1 = atan2( r11, r12 );
r2 = acos( r21 );
r3 = atan2( r31, r32 );
function qout = quatnormalize( q )
% QUATNORMALIZE Normalize a quaternion.
% N = QUATNORMALIZE( Q ) calculates the normalized quaternion, N, for a
% given quaternion, Q. Input Q is an M-by-4 matrix containing M
% quaternions. N returns an M-by-4 matrix of normalized quaternions.
% Each element of Q must be a real number. Additionally, Q has its
% scalar number as the first column.
%
% Examples:
%
% Normalize q = [1 0 1 0]:
% normal = quatnormalize([1 0 1 0])
%
% See also QUATCONJ, QUATDIVIDE, QUATINV, QUATMOD, QUATMULTIPLY,
% QUATNORM, QUATROTATE.
% Copyright 2000-2005 The MathWorks, Inc.
% $Revision: 1.1.6.1 $ $Date: 2005/11/01 23:39:35 $
qout = q./(quatmod( q )* ones(1,4));
function mod = quatmod( q )
% QUATMOD Calculate the modulus of a quaternion.
% N = QUATMOD( Q ) calculates the modulus, N, for a given quaternion, Q.
% Input Q is an M-by-4 matrix containing M quaternions. N returns a
% column vector of M moduli. Each element of Q must be a real number.
% Additionally, Q has its scalar number as the first column.
%
% Examples:
%
% Determine the modulus of q = [1 0 0 0]:
% mod = quatmod([1 0 0 0])
%
% See also QUATCONJ, QUATDIVIDE, QUATINV, QUATMULTIPLY, QUATNORM,
% QUATNORMALIZE, QUATROTATE.
% Copyright 2000-2005 The MathWorks, Inc.
% $Revision: 1.1.6.1 $ $Date: 2005/11/01 23:39:32 $
mod = sqrt(quatnorm( q ));
function qout = quatnorm( q )
% QUATNORM Calculate the norm of a quaternion.
% N = QUATNORM( Q ) calculates the norm, N, for a given quaternion, Q. Input
% Q is an M-by-4 matrix containing M quaternions. N returns a column vector
% of M norms. Each element of Q must be a real number. Additionally, Q has
% its scalar number as the first column.
%
% Examples:
%
% Determine the norm of q = [1 0 0 0]:
% norm = quatnorm([1 0 0 0])
%
% See also QUATCONJ, QUATDIVIDE, QUATINV, QUATMOD, QUATMULTIPLY,
% QUATNORMALIZE, QUATROTATE.
% Copyright 2000-2005 The MathWorks, Inc.
% $Revision: 1.1.6.1 $ $Date: 2005/11/01 23:39:34 $
if any(~isreal(q(:)))
error('aero:quatnorm:isnotreal','Input elements are not real.');
end
if (size(q,2) ~= 4)
error('aero:quatnorm:wrongdim','Input dimension is not M-by-4.');
end
qout = sum(q.^2,2);
测试文件**eularquat.m **
%matlab航空航天工具箱(Aerospace Toolbox)提供有:
%quat2angle函数实现四元数到欧拉角转换
%angle2quat函数实现欧拉角到四元数转换
%quat2angle调用示例
[yaw,pitch,roll]=quat2angle([1 0 1 0])
%angle2quat调用示例
q=angle2quat(0.7854,0.1,0)
结果:




























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










