概率统计·多维随机变量及其分布【二维随机变量、边缘分布、条件分布】

call me by ur name

已于 2022-10-31 19:48:47 修改

阅读量2.3k

点赞数 2

文章标签：概率论机器学习人工智能 1024程序员节

于 2022-10-15 14:36:03 首次发布

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/qq_61786525/article/details/127291273

版权

二维随机变量

在这里插入图片描述

(x,y)的左下部分

离散型

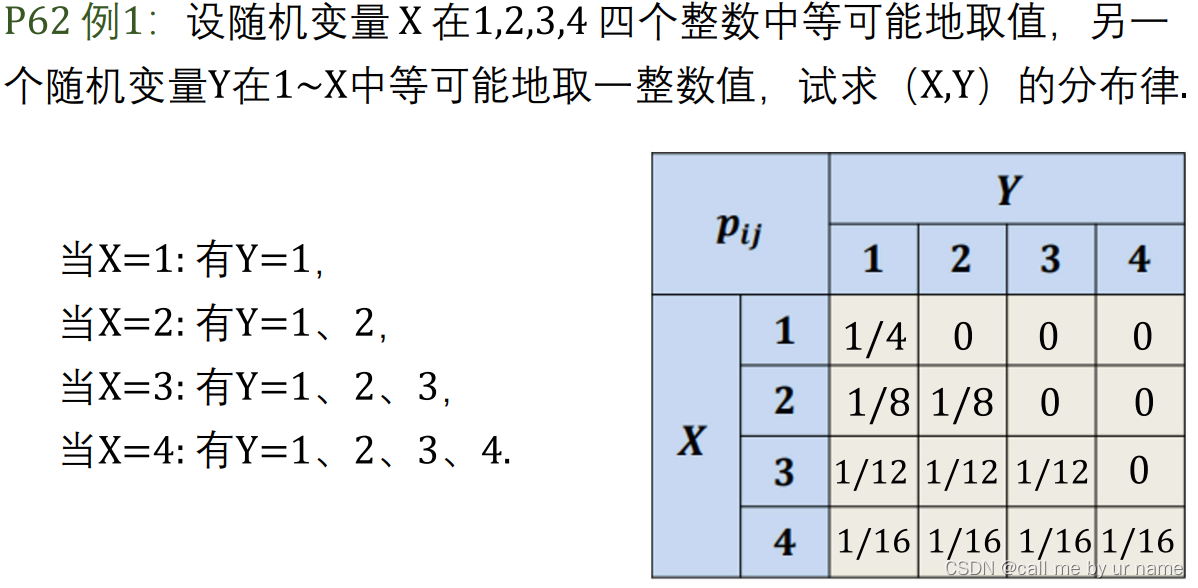
在这里插入图片描述

与一维不一样的是，二维离散在分布律中会写出概率为0的项

分布函数

在这里插入图片描述

就是将相应区域内的概率加起来

连续型

在这里插入图片描述

规范性还是要留意一下，有时会用到，用来求一些f(x)中的未知数k

例

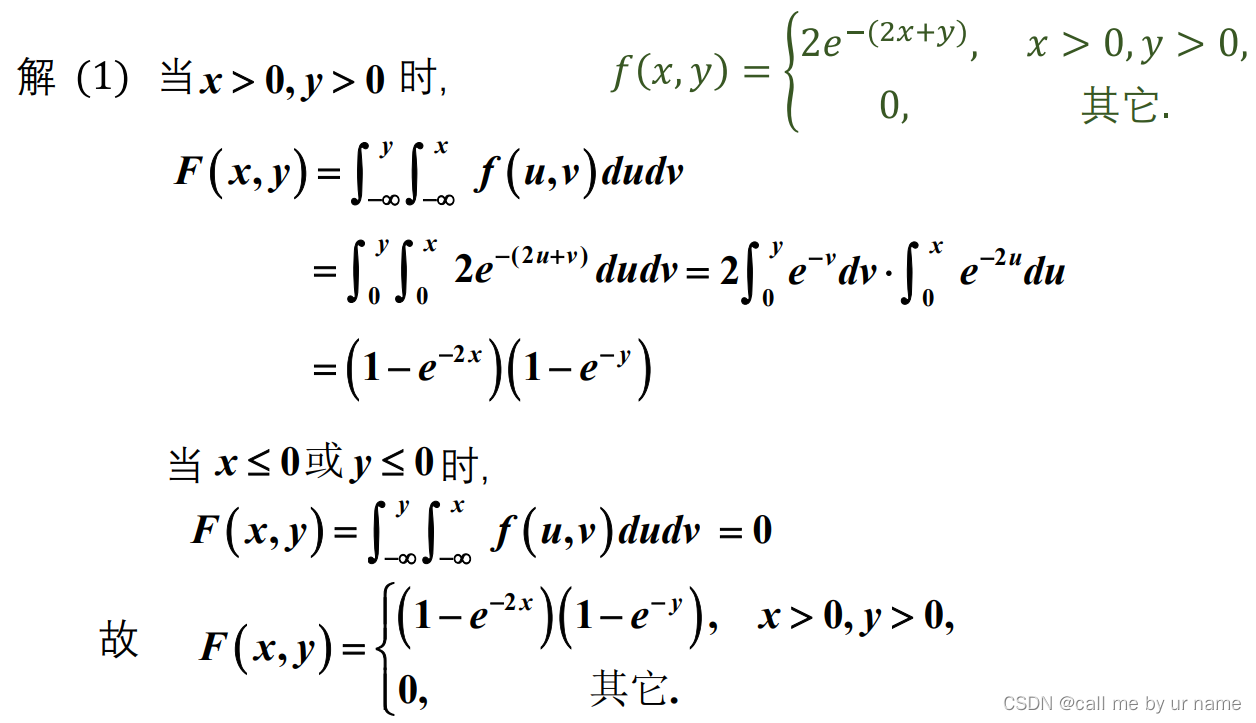
在这里插入图片描述

建议仔细思考一下，为什么第（1）问的二重积分上限不是+∞
因为二重积分的定义，F(x,y)=P{x≤X,y≤Y}。所以上限在这里已经确定了（2022.10.31，经过知识巩固后，发现细节）

注意二重积分的上下限，不能直接将f(u,v)代入2e^-(2x+y)，因为这个是在x>0，y>0的情况下的，所有要先变上下限
注意、注意、再注意。老师说考试的时候经常会错的😭😭😭

在这里插入图片描述

二重积分的积分方法还会吗😇
第（2）问，当多维分布函数概率出现时，可以想到用二重积分，在这个区域内的面积积分（2022.10.31期中复习）

在这里插入图片描述

第一问用了规范性

在这里插入图片描述

第2问同样要注意，不能直接将f(x,y)代入公式，先变上下限

边缘分布

在这里插入图片描述

就是默认一个量趋向正无穷，另一个变量可以改变
注意：F_x关于x的边缘分布函数右下角有x记号

离散型

在这里插入图片描述
也比较好理解，固定了一个变量x或y，另一个量从第一个i=1或者j=1开始到最后一个（趋向正无穷）
相当于将二维变成一维

分布函数

在这里插入图片描述
固定x_i，就是关于x的边缘分布函数
将在x_i条件下的所有y相加，极限相当于x_i的概率

在这里插入图片描述

连续型

在这里插入图片描述
~~这一页还是好好看看吧，虽然不难，但是好像也不是理解得非常透彻~~
注意概率密度
好好看看这一页吧

均匀分布

在这里插入图片描述

均匀分布——1/面积
不用特别知道那个3维的图

例

在这里插入图片描述

前面都忘记说了，二维首先要画图🥐🥐🥐
这个第一问用一下规范性即可，没什么好说的

在这里插入图片描述

边缘分布的上下限就用老师上课那样的方法（图上这种），f_x固定x观察y的范围，f_y固定y观察x的取值范围
这2个求边缘密度的题，虽然理解起来很简单，但是还是好好看一下，因为到自己实际写起来时，可能会出现意想不到的问题

正态分布

在这里插入图片描述

这个公式应该是不用记住的（毕竟有那么长，而且还复杂）

我个人估计考试考这个知识点的概率不是很大，因为这个知识点还是复杂的，不好考察边缘分布，通过边缘分布也不能确定联合分布

条件分布

离散型

在这里插入图片描述
注意划线部分的这种写法
简而言之——联合分布/边缘分布

性质

在这里插入图片描述
经典性质了属于是

例

在这里插入图片描述

注意范围

在这里插入图片描述
Y的边缘分布—— 因为联合分布实际上和m没有关系，所以∑就是单纯的求和，故最终结果的系数是(n-1)【从1——n-1】

X的边缘分布—— 是等比数列前n项的和

在这里插入图片描述
离散型最后结果可能与X和Y有关

连续型

在这里插入图片描述
注意划线部分的写法

在这里插入图片描述
一些基本关系，和一维的类似

例

在这里插入图片描述
注意这里需要2个定义域，第一个是为了分母的，第2个是为了条件概率的（要写出2个才不会被扣分）

在这里插入图片描述

这里的f_X(x)满足均匀分布（固定了X，y->+∞）【还是好好理解一下吧💦💦💦】

联合密度——条件*边缘 （注意定义域）
好好看一下f_Y(y)的求法

练习

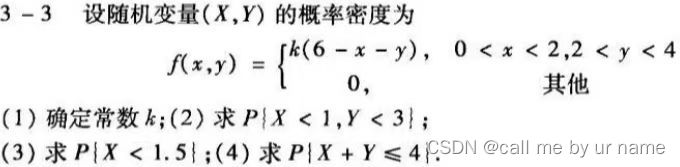
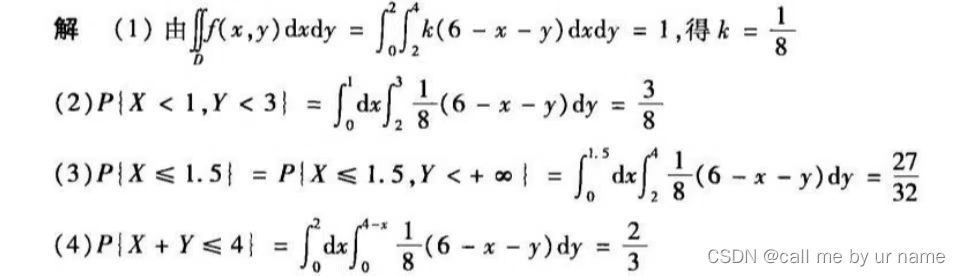
在这里插入图片描述

虽然这道题看上去很很很简单，但是我自己第一次做的时候，对于第1问的二重积分还不是很会积💢💢💢，因为x,y的定义域都是常数，而不是其中一个是另一个的相关的定义域

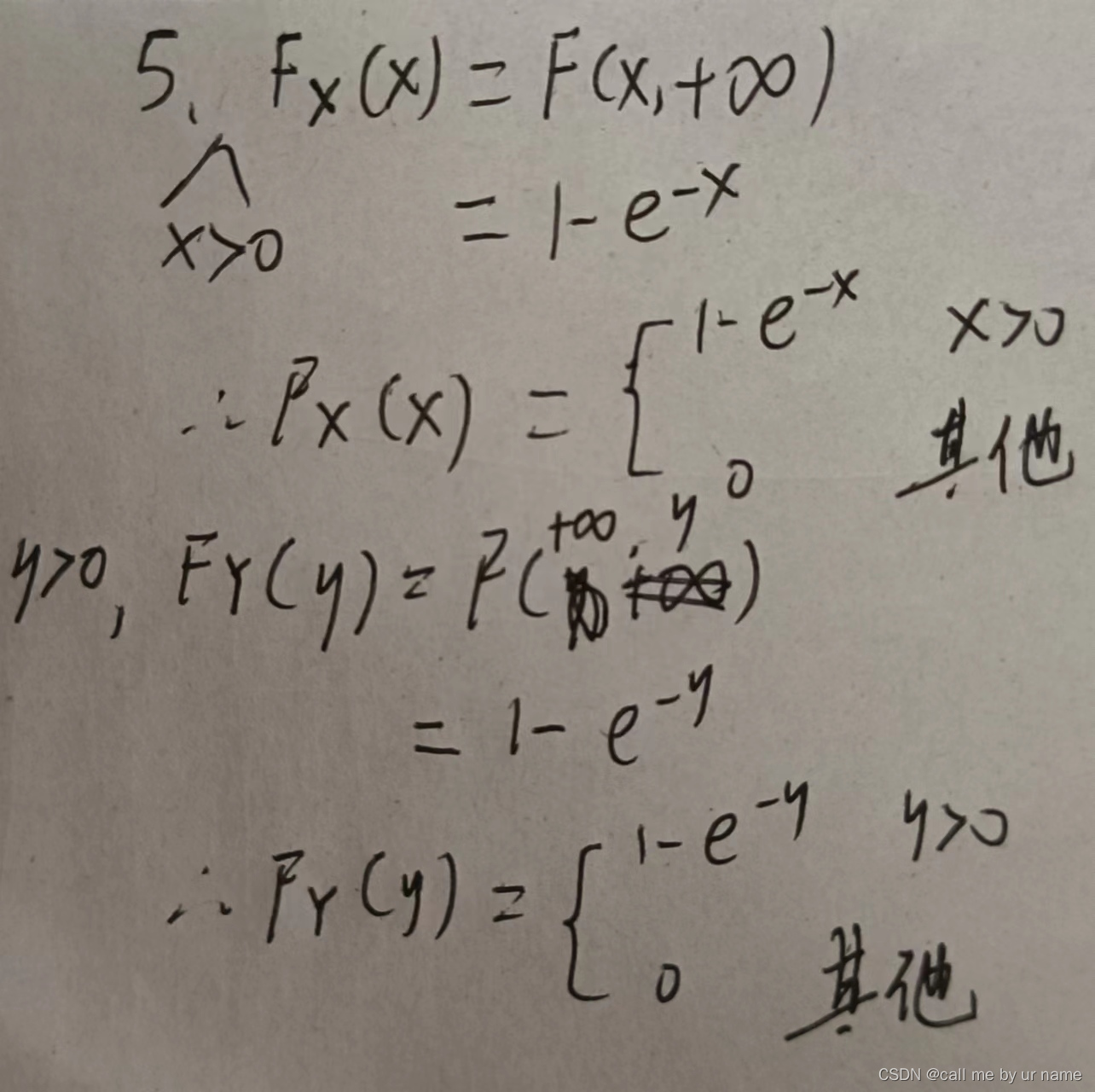
在这里插入图片描述

这道题看上去好像非常简单，但是我第一次做得时候真的分不清F_X和f_X的关系
所以仔细认真写写，切忌眼高手低
现在看来真的非常简单基础，心已累☕☕☕（2022.10.31期中复习，with listening to "Speak Softly Love"）
在这里插入图片描述

我的建议是画个图，清晰明了（自己第一次做，然后错了🧤🧤🧤）

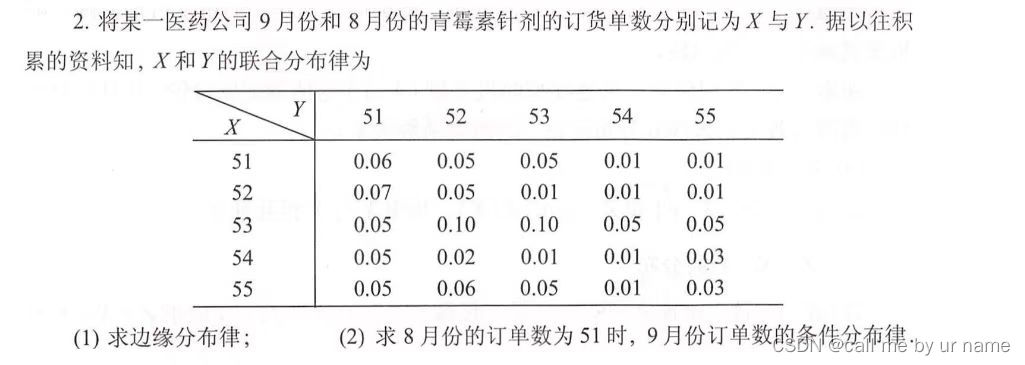
在这里插入图片描述

原来那个答案应该是错了，现在这个是正确的
~~第2问可以好好看看~~ 不太用了，现在感觉很简单了(2022.10.31)

在这里插入图片描述

条件概率要注意在前面加上y的取值范围（y作分母时），x的取值范围（x作分母时）
值得看看，对于知识的应用加深

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。