选频网络概述
在高频电子线路中,常以选频网络作为负载。选频网络能选出我们需要的频率分量和滤除不需要的频率分量。
选频网络分类:
1、振荡回路(由L、C组成,也称谐振回路):包括单振荡回路、耦合振荡回路。其中单振荡回路又分为串联和并联。
2、各种滤波器:例如LC滤波器、石英晶体滤波器、陶瓷滤波器、声表面波滤波器等。
重点讨论振荡回路。
串联谐振回路
单谐振回路:由信号源、电感线圈L、电容器C组成的组成的单个谐振回路。
串联谐振回路:信号源与电容、电感串接,就构成串联谐振回路。
R为电感线圈的损耗电阻,电容器的损耗一般可以忽略。
研究上述电路的阻抗:Z=R+jωL+jωC1=R+j(ωL−1/ωC)
阻抗模:
阻抗相角:
当信号的角频率为时发生谐振,此时总阻抗最小,为R;当回路出现谐振时的感抗或容抗称之为特性阻抗,用
表示:

谐振特性
(1)感性与容性
| 纯阻性 | ||
| 感性 | ||
| 容性 |
(2) 谐振时电流值(幅值)最大,且与电压源同相。
(3)在谐振点及其附近,电路电阻R是决定电流大小的主要因素;当频率远离谐振点时,电抗远大于电阻,这时电路电流大小几乎与R没什么关系。
谐振频率
阻抗在某一特定频率上有最小值,而偏离这个频率的时候阻抗将迅速增大,单振荡回路这种特性称为谐振特性,做个特定频率称为谐振频率。
品质因数
谐振时的回路感抗值(容抗值)与回路电阻R的比值定义为回路的品质因数,用Q来表示。它表示回路损耗的大小。
当谐振时,电感电压为:
电容电压为:
在谐振时,L与C上的电压大小相等,相位正好相差180° ,相互抵消。电容电感的电压大小也是信号源电压大小的 Q 倍。高频电子线路的Q值往往为几十到几百,因此在选择器件耐压参数时不仅要考虑电压源数值,还要考虑Q值。这是串联谐振时所特有的现象,所以串联谐振又称电压谐振。
广义失谐系数
广义失谐是表示回路失谐大小的量。
定义为:
其中X为失谐时的电抗,括号内为狭义失谐。
当
时,即失谐不大时:
,其中
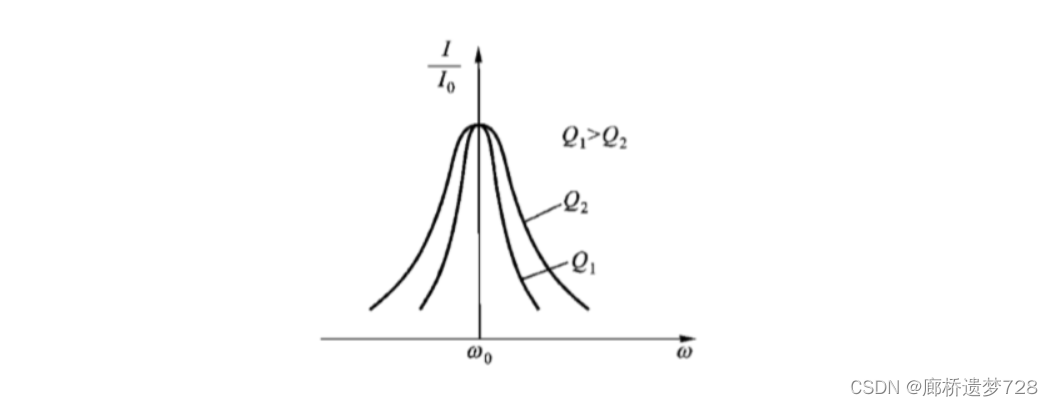
谐振曲线
通过分析电路结构可得到总阻抗Z的大小,进而得到电流的大小,其电流与角频率ω有关。将电流与ω之间的关系称为谐振曲线。可用N(f)表示谐振曲线的函数。
由于电流的表达式中含有电压这样一个参数,对分析有影响,通常取相对的电流来作为谐振曲线。
,其中I为失谐处电流,Io为谐振处电流。
引入广义失谐系数可得:
其模值为:

得到串联谐振回路的谐振曲线:
Q值大,曲线尖锐,选择性好;Q值小,曲线钝,通带宽,选择性差。
通频带
为了衡量谐振回路的选择性,引入通频带的概念。
定义:回路外加电压的幅值不变时,改变频率,回路电流I下降到Io的0.707倍时所对应的频率范围称为通频带。

在通频带的边界角频率处,回路中所损耗的功率为谐振时的一半,所以这两个角频率又称为半功率点。在半功率点处,=1或-1。
通频带的绝对值为:或
;
通频带的相对值为:
相频特性曲线
指回路电流的相角随频率的变化的曲线。
相位特性曲线表达式为:
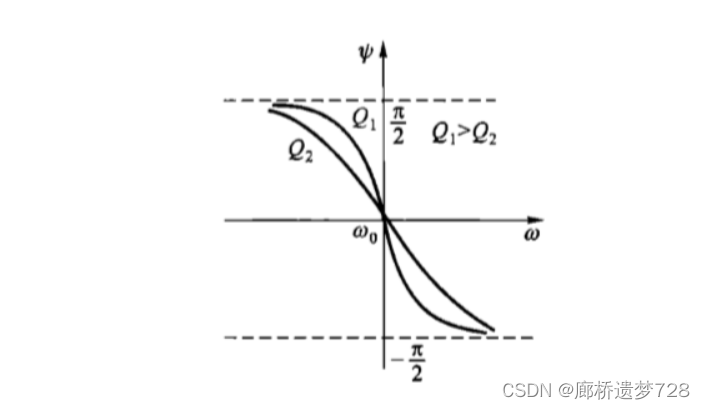
串联谐振回路通用相位特性曲线:










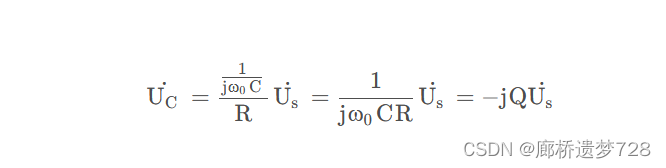
















 3670
3670

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








