由于高中数学,以及大学数学已经还给老师了,所以写的有点基础。
均方误差

期望=估计值=均值 期望一般的表示为E(X), 这里面的X表示的是事件。
为了能让这个生动一点

现在应该回忆起了高中数学的期望值的算法,也就是某一个事件X.
现在要求平均正点率,如果平常来想的话,就直接把三种情况的正点率相加,然后除以3就可以了,但是在这里给出了每一种情况出现的概率,也就是给每一种情况赋予了权重,使得权重不再是1/n了。因此我们就可以0.97x 10/(10+20+10)+0.98x20/40+0.99x10/40
这个是一个生活种的例子。
对于不同的变量:离散型随机变量和连续型随机变量,它们求解期望的公式不同,但是它们内在是相同的。具体怎么从离散推导到连续,可以看这个视频
https://www.bilibili.com/video/BV1pz411B7ZU?spm_id_from=333.337.search-card.all.click&vd_source=407f1c674163347577a4d2596de4e13d

上面那个离散型的比较好理解,就是这件事发生的某一种情况x它对应的概率。连续型的话,其实f(x)dx就是概率,f(x)是概率密度函数,dx可以想成是每一个频率直方图的每一格。
在这里,我们要求均方差,也就是方差的平均值,那也就是期望,所以用E来表示。
2.2 是离散型随机变量的写法 拆开 来写的话,就是(f(x)-y)21/m + (f(x)-y)^21/m ……
在这里面(f(x)-y)^2 相当于是我们要求的目标,所以就很容易推到到下面那一步,也就是f(x)dx 就相当于是概率。积分相当于求和
错误率和精确率
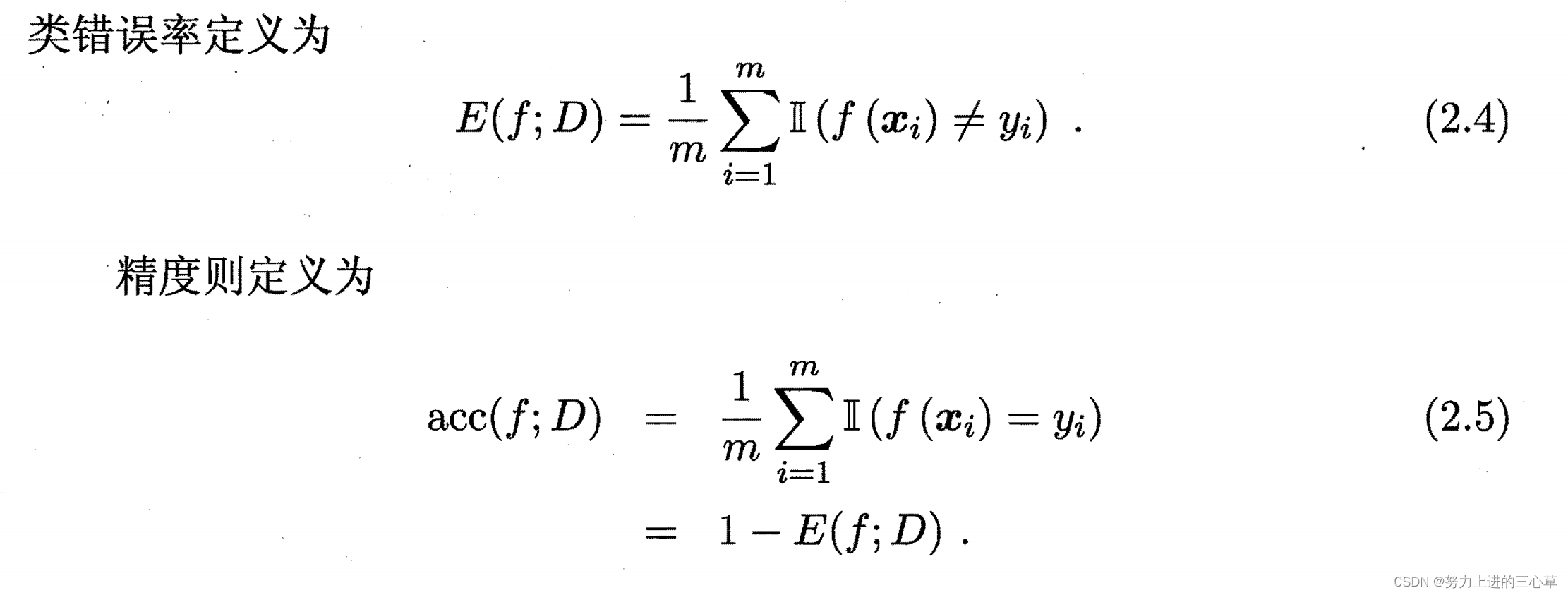
这里面有一个指示函数,如果它是真的话,那就是1,如果是假的话,就是0.知道这个之后就很容易理解。下面对于概率密度函数和上面的均方差的理解是一样的。
查准率,查全率和混淆矩阵
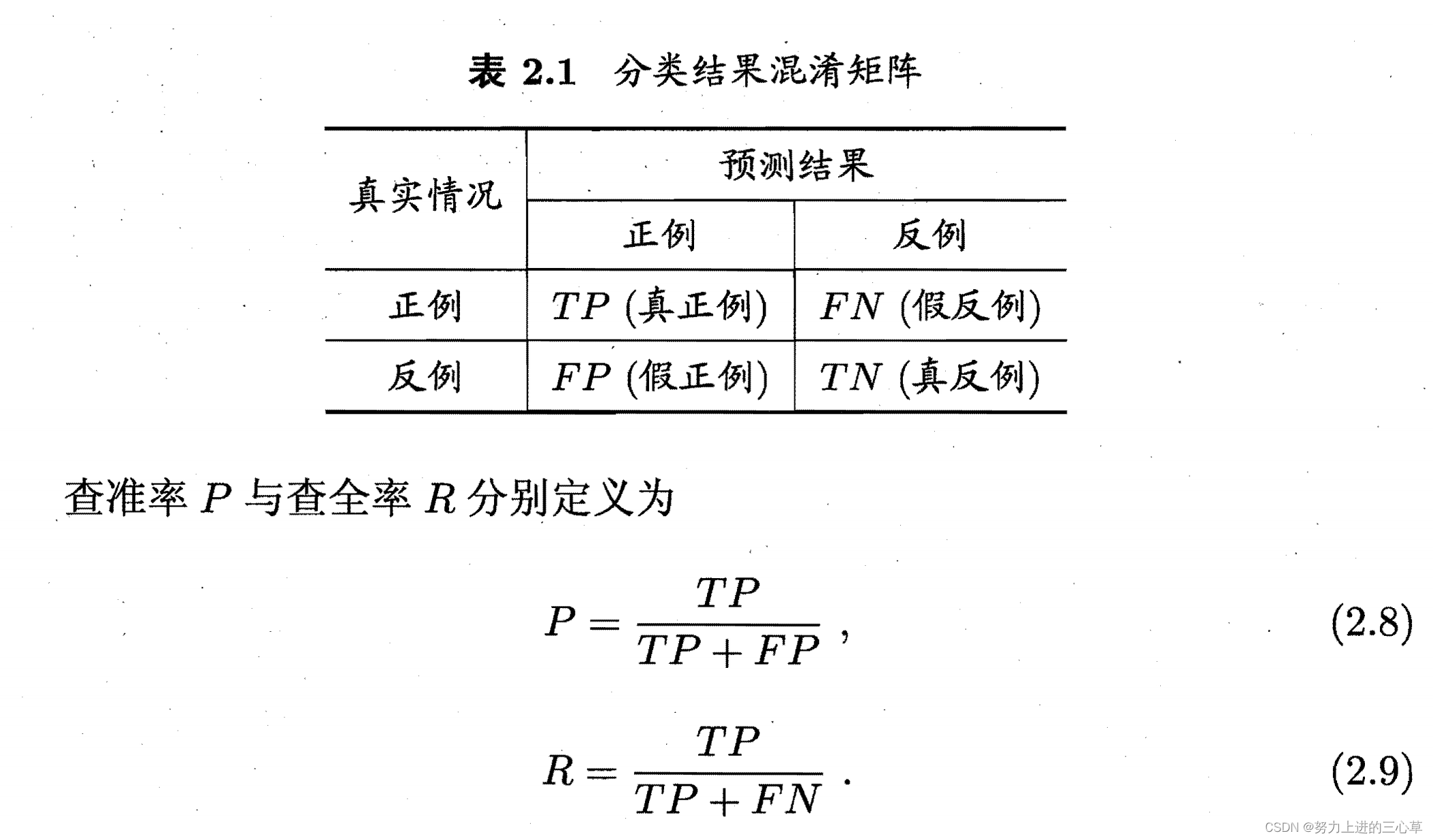
对于这个的话,首先得自己写出混淆矩阵,然后根据混淆矩阵得到precision (P) 和召回率 (R)recall
在这里面查全率就是召回率。precision和recall通常是一对矛盾的指标,两个并不能同时都很高。
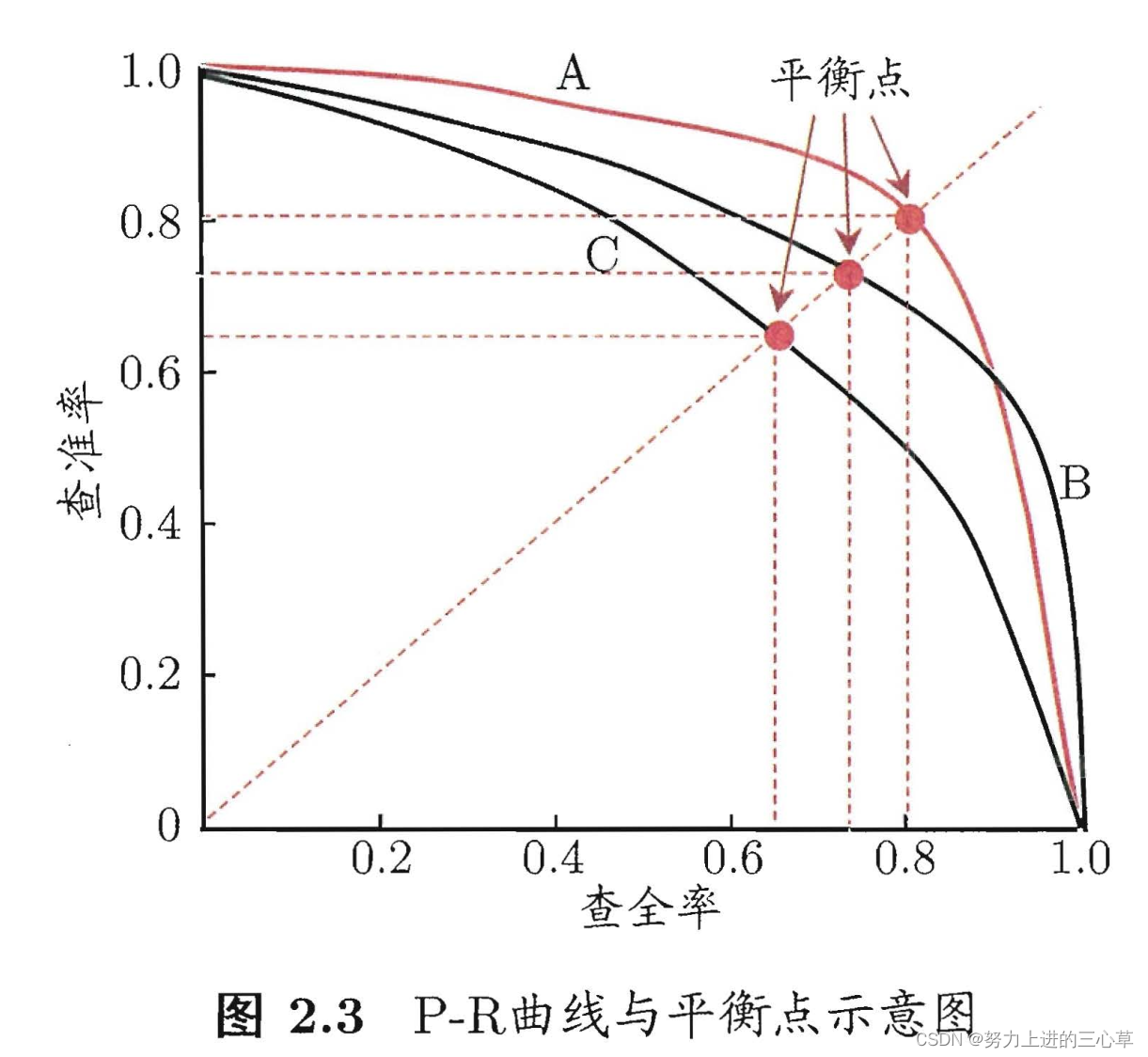
P-R曲线
P-R图的横坐标是recall,纵坐标是precision。
老师的brie2的文章种就有一个P-R曲线的图

从上面这张图发现,BRIE2的P-R曲线完全包住了另外两个软件,说明它的performance比较好。
对于这种图,有两种可以看的指标,一种是曲线下面积,另外一个是BEP,也就是平衡点,在这个平衡点的时候precision等于recall.,实际来说也就是画一条斜率为1,过原点的直线。然后查看它与P-E曲线的相交情况。如下面这张图所示。
F1 Fβ
F1 是和precision以及recall,还有P-R曲线紧密相连的。它的定义为

这个式子的来历为

为了能够满足一些特殊情况的需要,让查全率或者查准率更重要一些,引入了Fβ

当β=1时就是F1,当β>1时,recall有更大的影响,当β<1时,precision有更大的影响。
宏查全率,宏查准率,宏F1;微查全率,微查准率,微F1
这两组概念的区别就是宏是得到每一个二分类的混淆矩阵,基于这些混淆矩阵分别得到P,R和F1.然后对这些分别得到的P,R,F1求平均值。
微就是先对多个混淆矩阵种相应位置上的值求一个平均值,最终得到一个总的混淆矩阵,然后再根据这个总的混淆矩阵求平均值。
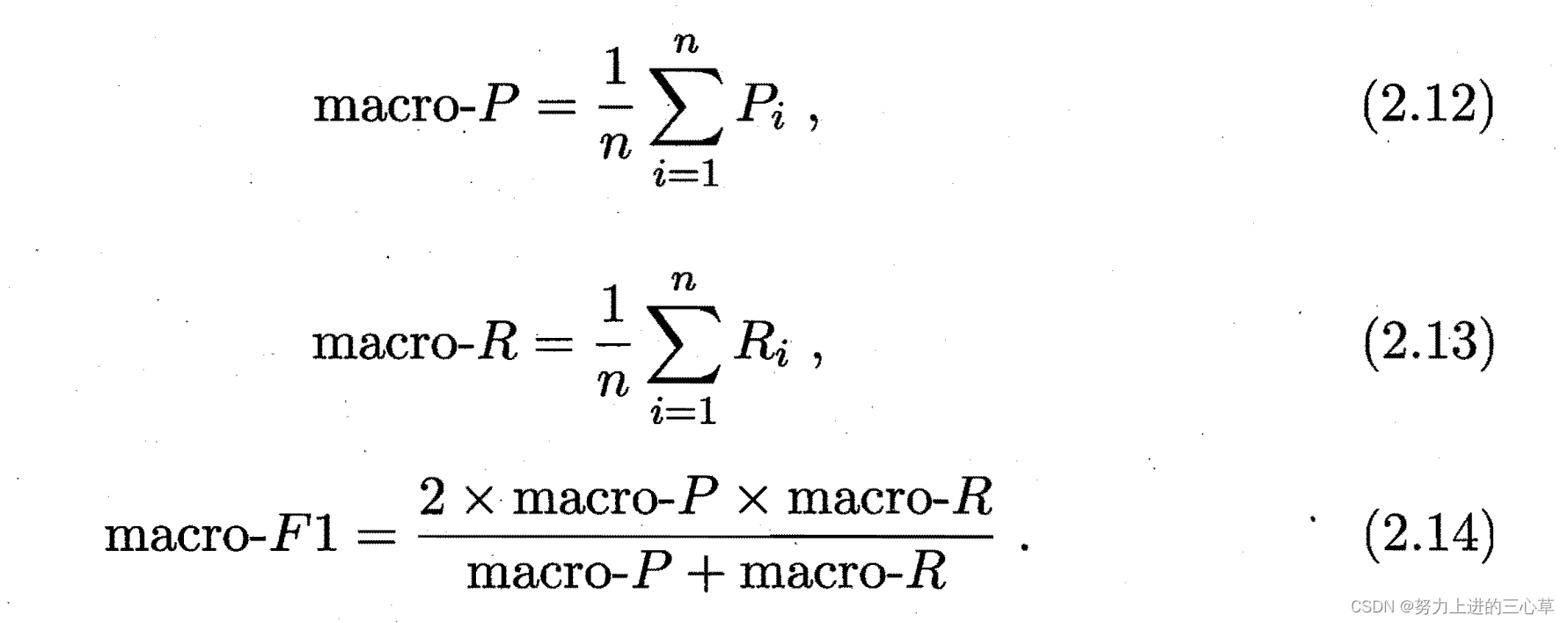

ROC curve 和AUC
首先一定要知道ROC curve的横纵坐标分别是什么,它的横坐标是假正例率,纵坐标是真正例率。

可以注意到的是,这里面的真正例率就是我们的precision。
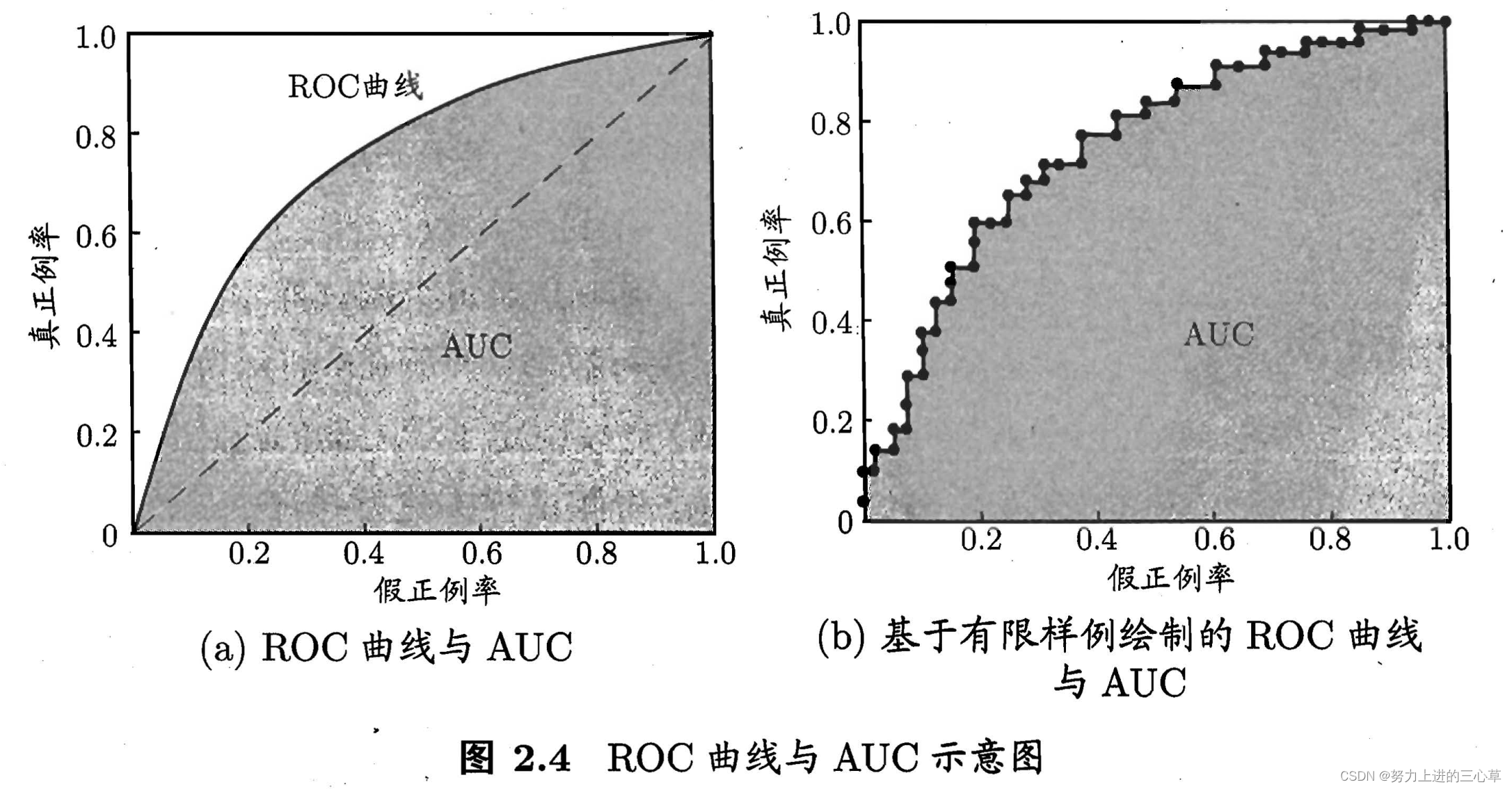
这个ROC曲线也是我们经常使用的,对角线的部分是相当于瞎猜。
感觉这个AUC的计算过程自己还没有完全理解。
但是可以调用函数直接算出来。。。

这个是老师的BRIE2的ROC curve。
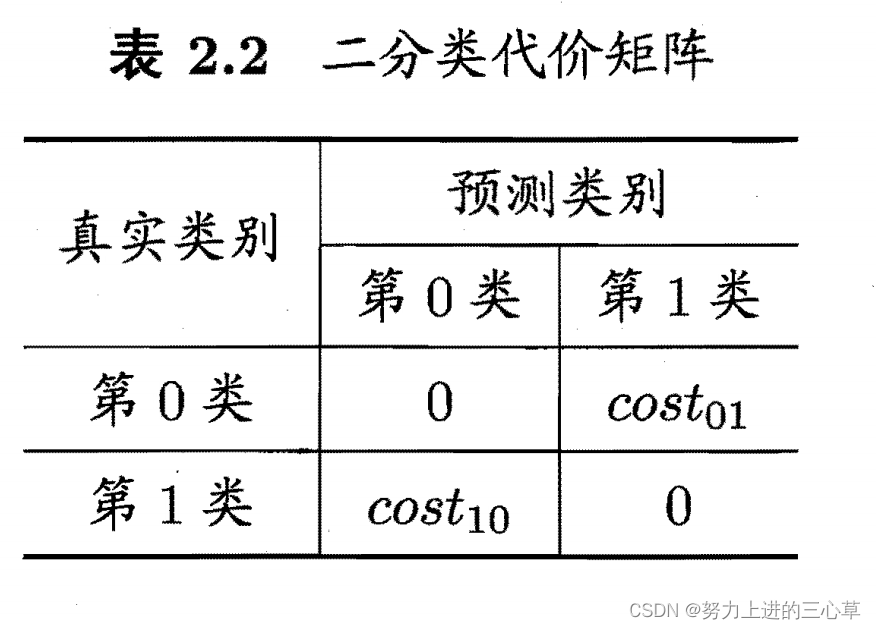
代价矩阵;代价敏感错误率;代价曲线图
这其实的意思就是给错误的情况设置一些权重。
代价敏感错误率的公式为
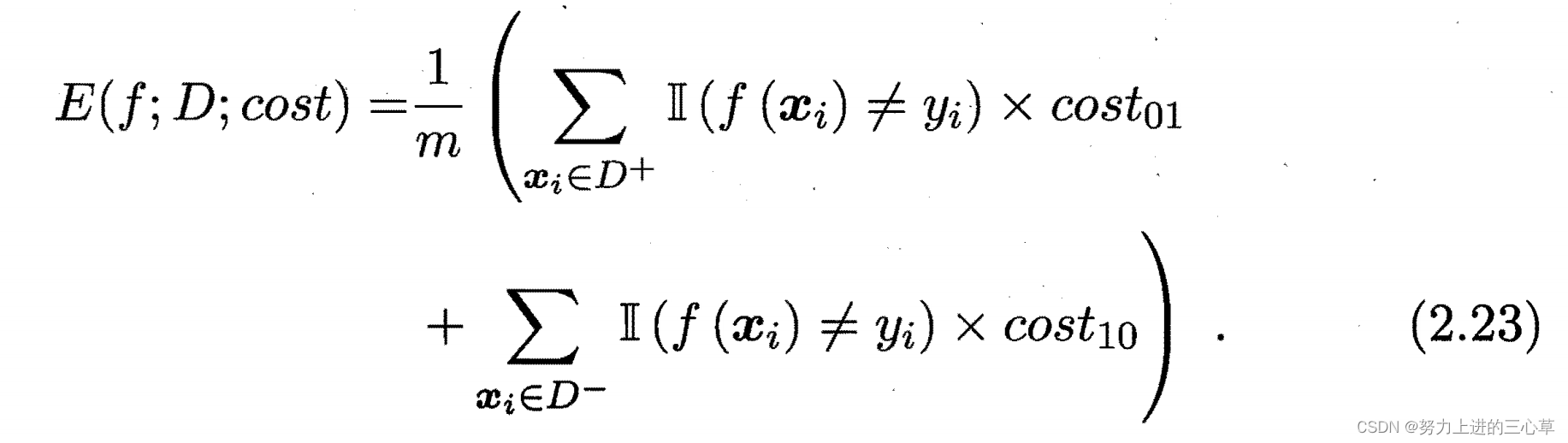
代价曲线图种的横轴和纵轴的定义


感觉这个代价曲线我们平时很少用到?























 1916
1916

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








