[统计学笔记] （十）一元线性回归

最新推荐文章于 2025-02-10 18:05:59 发布

梅森上校

最新推荐文章于 2025-02-10 18:05:59 发布

阅读量9.3k

点赞数 2

分类专栏：数据分析

本文为博主原创文章，未经博主允许不得转载。

本文链接：https://blog.csdn.net/seagal890/article/details/105594665

版权

本文详细介绍了统计学中的一元线性回归，包括基本术语、相关与回归分析的概念，以及一元线性回归的定义。通过相关图表、相关系数和散点图等工具，分析变量间的线性关系强度，并探讨了回归分析要解决的问题，如确定变量间关系、关系强度和估计预测。同时，文中提供了一个实例来解释如何进行相关分析和一元线性回归的运用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

（十）一元线性回归

基本术语

回归这一术语最早来源于生物遗传学，由高尔顿（Francis Galton）引入。

回归的解释：回归分析是研究某一变量（因变量）与另一个或多个变量（解释变量、自变量）之间的依存关系，用解释变量的已知值或固定值来估计或预测因变量的总体平均值。

因变量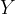： $\large Y$
自变量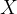： $\large X$ 或 $\large X_{1}$ ， $\large X_{2}$ ， $\large X_{3}$ ，……等等。

数值型自变量和数值型因变量之间关系的分析方法，就是相关与回归分析。

相关与回归是处理变量之间关系的一种统计方法。如果研究的是两个变量之间的关系，则称为简单相关与简单回归分析；如果研究的是两个以上变量之间的关系，则称为多元相关与多元回归分析。

从变量之间的关系形态来看，有线性相关与线性回归分析及非线性相关与非线性回归分析。

变量之间的关系

变量之间的关系可以划分为：函数关系和相关关系。

函数关系是一一对应的关系。

变量之间存在的不确定的数量关系称为相关关系。

例子：

相关关系的描述与测度

相关分析就是对两个变量之间线性关系的描述与度量，它要解决的问题包括：

变量之间是否存在关系？
如果存在关系，他们之间是什么样的关系？
变量之间的关系强度如何？
样本所反映的变量之间的关系能否代表总体变量之间的关系？

为了解决这些问题，在进行相关分析时，对总体主要有两个假定：

第一：两个变量是线性相关的；

第二：两个变量都是随机变量；

确定相关关系的存在，相关关系呈现的形态和方向，相关关系的密切程度。其主要方法是绘制相关图表和计算相关系数。
1）相关表
编制相关表前首先要通过实际调查取得一系列成对的标志值资料作为相关分析的原始数据。
相关表的分类：简单相关表和分组相关表。单变量分组相关表：自变量分组并计算次数，而对应的因变量不分组，只计算其平均值；该表特点：使冗长的资料简化，能够更清晰地反映出两变量之间相关关系。双变量分组相关表：自变量和因变量都进行分组而制成的相关表，这种表形似棋盘，故又称棋盘式相关表。
2）相关图
利用直角坐标系第一象限，把自变量置于横轴上，因变量置于纵轴上，而将两变量相对应的变量值用坐标点形式描绘出来，用以表明相关点分布状况的图形。相关图被形象地称为相关散点图。因素标志分了组，结果标志表现为组平均数，所绘制的相关图就是一条折线，这种折线又叫相关曲线。
3）相关系数
1、相关系数是按积差方法计算，同样以两变量与各自平均值的离差为基础，通过两个离差相乘来反映两变量之间相关程度；着重研究线性的单相关系数。
2、确定相关关系的数学表达式。
3、确定因变量估计值误差的程度。

在进行相关分析时，首先需要绘制散点图来判断变量之间的关系形态，如果是线性关系，则可以利用相关系数来测度两个变量之间的关系强度，然后对相关系数进行显著性检验，以判断样本所反映的关系是否代表两个变量总体上的关系。

根据散点图，当自变量取某一值时，因变量对应为一概率分布，如果对于所有的自变量取值的概率分布都相同，则说明因变量和自变量是没有相关关系的。反之，如果，自变量的取值不同，因变量的分布也不同，则说明两者是存在相关关系的。

两个变量之间的相关程度通过相关系数 $\large r$ 来表示。相关系数 $\large r$ 的值在-1和1之间，但可以是此范围内的任何值。

正相关时， $\large r$ 值在0和1之间，散点图是斜向上的，这时一个变量增加，另一个变量也增加；

负相关时， $\large r$ 值在-1和0之间，散点图是斜向下的，此时一个变量增加，另一个变量将减少。

$\large r$ 的绝对值越接近1，两变量的关联程度越强，

$\large r$ 的绝对值越接近0，两变量的关联程度越弱。