基于传递函数的汽车瞬态响应特性仿真

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

前言

提示：这里可以添加本文要记录的大概内容：

本篇博文主要用来记录汽车系统动力学课程的学习，仅供课程阶段参考，与实际工程应用还有较大距离。
本实例主要有以下任务。
1.建立汽车横摆角速度传递函数。
2.绘制不同车速下的汽车横摆角速度时域特性曲线。
3.绘制不同轮胎侧偏刚度下的汽车横摆角速度时域特性曲线。
4.绘制不同转动惯量下的汽车横摆角速度时域特性曲线。
5.绘制不同车速下的汽车横摆角速度频率特性曲线。
6.绘制不同轮胎侧偏刚度下的汽车横摆角速度频率特性曲线。
7.绘制不同转动惯量下的汽车横摆角速度频率特性曲线。

一、汽车系统仿真参数

二、建模及仿真

1.建立汽车横摆角速度传递函数

根据质心侧偏角度的定义：
$$\beta =\frac{v}{u}（1）$$
汽车横向的加速度为：
$$a_y=\dot{v}+u{\omega }_r（2）$$
前轮的侧偏角为：
$${\alpha }_1=\beta +\frac{a{\omega }_r}{u}-\delta （3）$$
后轮的侧偏角为：
$${\alpha }_2=\beta +\frac{b{\omega }_r}{u}（4）$$
根据牛顿第二定律：
$$m(\dot{v}+u{\omega }_r)=k_1{\alpha }_1+k_2{\alpha }_2（5）$$
$$I_z{\dot{w}}_r=a{k}_1{\alpha }_1-b{k}_2{\alpha }_2$$
将公式（1）（2）（3）（4）代入（5）中并转为矩阵形式：

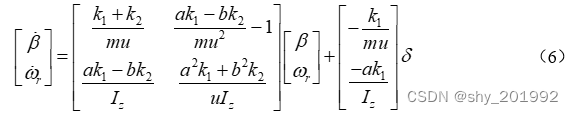
对上述矩阵进行Laplace变换：

令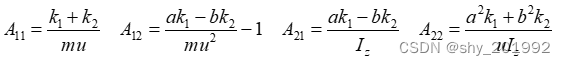

令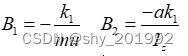

则上式转化为：

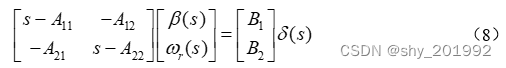
求解得到：
$$\frac{\beta (s)}{\delta (s)}=\frac{(s-A_{22})B_1+A_{12}{B}_2}{(s-A_{11})(s-A_{22})-A_{12}{A}_{21}}（9）$$
$$\frac{{\omega }_r(s)}{\delta (s)}=\frac{(s-A_{11})B_2+A_{21}{B}_1}{(s-A_{11})(s-A_{22})-A_{12}{A}_{21}}（10）$$

2.绘制不同车速下的汽车横摆角速度时域特性曲线

车速分别选取10m/s、20m/s和30m/s；在仿真时间0s时给前轮一个阶跃信号，使前轮转角从0°转到10°，并保持不变。
解：根据公式（6）在MATLAB中编程lianxi52.m，运行后得到结果如图（2）：

图2 不同速度下的汽车横摆角速度时域特性曲线
根据仿真结果来看，随着车速的增加，汽车首次达到稳态横摆角速度的反应时间减小；汽车最大的横摆角速度大于稳态值的幅度，即超调量，随着车速的增大而增加；汽车进入稳态值95%～105%所需的稳定时间，随着车速的增大而增加。

3.绘制不同轮胎侧偏刚度下的汽车横摆角速度时域特性曲线

选取车速为20m/s，前、后轮胎综合侧偏刚度由-23147N/rad、-38318N/rad变为 -33124N/rad、-69972N/rad，其他条件不变。
解：根据公式（6）在MATLAB中编程lianxi53.m，运行后得到结果如图（2）：

图3 不同轮胎侧偏刚度下的汽车横摆角速度时域特性曲线
根据仿真结果来看，随着轮胎侧偏刚度绝对值的增加，汽车首次达到稳态横摆角速度的反应时间减小；汽车横摆角速度的超调量，随着轮胎侧偏刚度绝对值的增大而减小；汽车进入稳态值95%～105%所需的稳定时间，随着轮胎侧偏刚度绝对值的增大而减小。

4.绘制不同转动惯量下的汽车横摆角速度时域特性曲线

选取车速为20m/s，转动惯量由10437 kg·m2变为5537 kg·m2和20237 kg·m2，其他条件不变。
解：根据公式（6）在MATLAB中编程lianxi54.m，运行后得到结果如图（4）：

图4 不同转动惯量下的汽车横摆角速度时域特性曲线
根据仿真结果来看，随着汽车转动惯量的增加，汽车首次达到稳态横摆角速度的反应时间减小；汽车横摆角速度的超调量，随着汽车转动惯量的增大而减小；汽车进入稳态值95%～105%所需的稳定时间，随着汽车转动惯量的增大而增大。

5.绘制不同车速下的汽车横摆角速度频率特性曲线

车速分别选取10m/s、20m/s和30m/s。
解：根据公式（6）在MATLAB中编程lianxi55.m，运行后得到结果如图（5）：

图5 不同速度下的汽车横摆角速度频域特性曲线
对图（5）中的结果整理后得到表（1）的数据：

根据表（1）的结果，随着车速的增加，稳态的横摆角速度增益减小，0.1Hz和0.6Hz对应的相位角增大，意味着汽车对转向盘转角.的响应速度变慢。
6.绘制不同轮胎侧偏刚度下的汽车横摆角速度频率特性曲线
选取车速为20m/s，前、后轮胎综合侧偏刚度由-23147N/rad、-38318N/rad变为 -33124N/rad、-69972N/rad，其他条件不变。
解：根据公式（6）在MATLAB中编程lianxi56.m，运行后得到结果如图（6）：

图6 不同轮胎侧偏刚度下的汽车横摆角速度时域特性曲线
对图（6）中的结果整理后得到表（2）的数据：

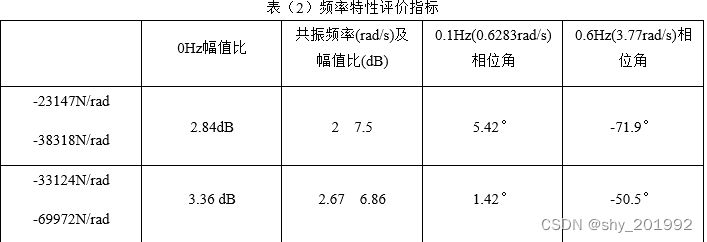
根据表（2）的结果，随着轮胎侧偏刚度绝对值的增加，稳态的横摆角速度增益增大，0.1Hz和0.6Hz对应的相位角减小，意味着汽车对转向盘转角.的响应速度变快。

7.绘制不同转动惯量下的汽车横摆角速度频率特性曲线
选取车速为20m/s，转动惯量由10437 kg·m2变为5537 kg·m2和20237 kg·m2，其他条件不变。
解：根据公式（6）在MATLAB中编程lianxi57.m，运行后得到结果如图（7）：

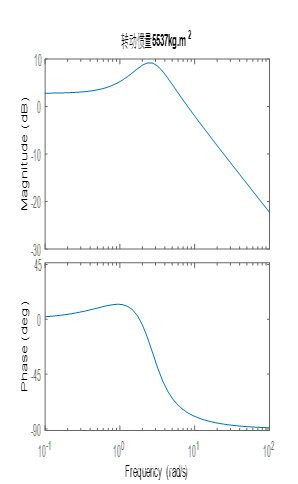
图7 不同转动惯量下的汽车横摆角速度频域特性曲线
对图（7）中的结果整理后得到表（3）的数据：

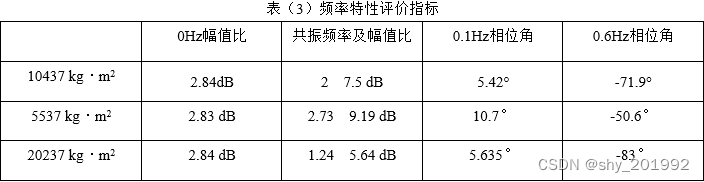
根据表（3）的结果，随着汽车转动惯量的增加，稳态的横摆角速度增益几乎不变，0.1Hz对应的相位角减小，意味着汽车对缓慢转动转向盘的响应速度变快；0.6Hz对应的相位角增大，意味着汽车对快速转动转向盘的响应速度变慢。

三、文件脚本附录

simulink模型搭建的具体内容在本篇文章附件，可在matlab2015b及以上版本打开并运行，仅供参考。