文章目录
飞行器传感器
无人机的常用导航方式是惯性导航+GPS,所以无人机上的常用传感器也是围绕这两者展开的,惯性导航一般包括三轴加速度计、三轴陀螺仪、三轴磁力计,再加上GPS构成了机载传感器的主体,除此之外还有超声波测距传感器、激光测距传感器、空速计、气压计、视觉传感器等。
加速度计
加速度计用来测量飞行器质心的线加速度。其一般放在飞机的重心处(放三个),传感器的敏感轴处于机体轴的三个轴向,因此可感受和测量飞行器三个轴向的线加速度。
若敏感轴与机体坐标系中的 z z z轴重合,则线加速度传感器测量飞行器的法向加速度;若敏感轴与 x x x或 y y y轴重合,则分别测量飞行器的纵向加速度 a x a_x ax或侧向加速度 a y a_y ay。
当无人机静止时,加速度计测得的就是重力加速度,所以在实际使用时,我们都需要去掉重力加速度计的值。
其也可代替迎角或侧滑角传感器,近似测量飞机的迎角或侧滑角。另外,当作用在无人机上的外力远小于重力时,加速度计还可以用来测量姿态角,因为当无人机倾斜时,加速度计在体轴系下测得的各项加速度大小跟无人机的姿态角以及重力加速度的值有关,而重力加速度的值已知,我们就可以根据三轴加速度的大小来计算出无人机的姿态信息(航向除外,因为该平面与重力加速度的方向垂直,重力加速度没有在该平面上的分力)。
简单式线加速度传感器
简单的线加速度传感器主要由弹簧和弹簧所支撑的可动质量块 m m m以及电位计式信号变换器和阻尼器等部分组成。
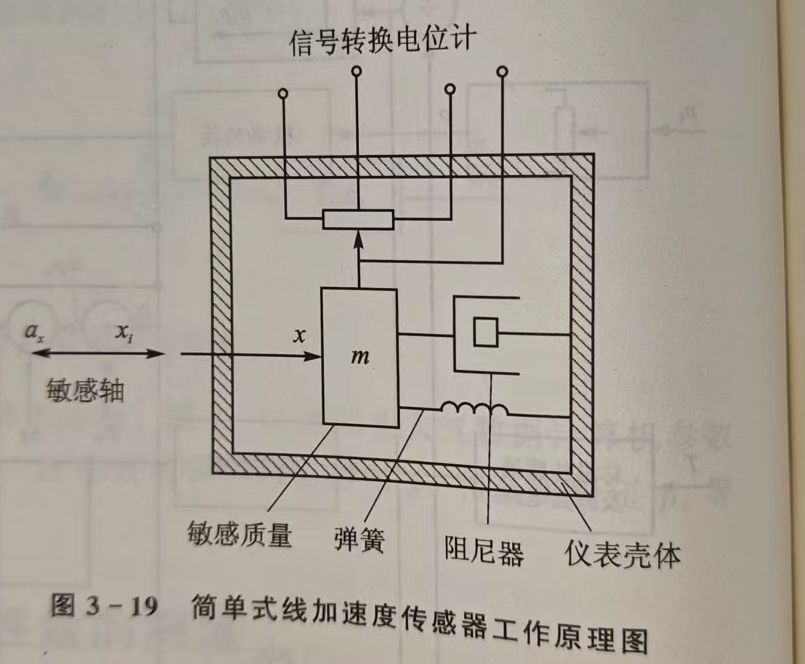
假定飞行器在惯性空间内运动,其位移量为
x
i
x_i
xi, 相应的线加速度为
a
x
=
d
2
x
i
d
t
2
a_x=\frac{d^2 x_i}{d t^2}
ax=dt2d2xi。由于线加速度传感器通过仪表壳体与飞行器固连,因此飞行器的位移量也就是仪表壳体的位移量,而其线加速度就是线加速度传感器的输入量。仪表中的敏感质量块具有惯性,相对惯性空间有运动,其位移量为
z
z
z;电刷固连与质量块上,其在仪表壳体内相对电位计骨架的位移量为
x
x
x,所以线加速度传感器的输出量
x
=
z
−
x
i
x=z-x_i
x=z−xi。
忽略弹簧质量,电位计摩擦力,有
m d 2 z d t 2 + K g d x d t + K x = 0 m \frac{\mathrm{d}^2 z}{\mathrm{~d} t^2}+K_{\mathrm{g}} \frac{\mathrm{d} x}{\mathrm{~d} t}+K x=0 m dt2d2z+Kg dtdx+Kx=0
其中 K g K_g Kg为阻尼系数, K x Kx Kx为弹簧力。将 x = z − x i x=z-x_i x=z−xi代入得
d 2 x d t 2 + K g m d x d t + K m x = − d 2 x i d t 2 \frac{\mathrm{d}^2 x}{\mathrm{~d} t^2}+\frac{K_{\mathrm{g}}}{m} \frac{\mathrm{d} x}{\mathrm{~d} t}+\frac{K}{m} x=-\frac{\mathrm{d}^2 x_i}{\mathrm{~d} t^2} dt2d2x+mKg dtdx+mKx=− dt2d2xi
将 a x = − d 2 x i d t 2 a_x=-\frac{d^2 x_i}{d t^2} ax=−dt2d2xi代入得到传递函数为
x ( s ) a x ( s ) = − 1 s 2 + 2 ζ ω 0 s + ω 0 2 \frac{x(s)}{a_x(s)}=-\frac{1}{s^2+2 \zeta \omega_0 s+\omega_0^2} ax(s)x(s)=−s2+2ζω0s+ω021
式中
ζ
=
K
g
2
m
K
\zeta=\frac{K_{\mathrm{g}}}{2 \sqrt{m K}}
ζ=2mKKg为相对阻尼系数,
ω
0
=
K
m
\omega_0=\sqrt{\frac{K}{m}}
ω0=mK为固有频率。
在稳态时,有
x
=
−
m
K
a
x
x=-\frac{m}{K} a_x
x=−Kmax,如果将输出电压
U
=
K
U
x
U=K_Ux
U=KUx代入有
U
=
−
K
U
m
K
a
x
U=-\frac{K_U m}{K} a_x
U=−KKUmax
单位加速度所产生的相对位移量定义为传感器的分辨率,即
d x d a x = − m K = − 1 ω 0 2 \frac{\mathrm{d} x}{\mathrm{~d} a_x}=-\frac{m}{K}=-\frac{1}{\omega_0^2} daxdx=−Km=−ω021
弹簧刚度越小,质量块质量越大,则传感器分辨率就越高,即更灵敏。
不足
电刷与电位计摩擦力较大,且质量块易受震动等因素的影响,弹簧易受温度影响,线性特性较差,灵敏度较低。
MEMS加速度计
MEMS加速度计是最常用的类型之一,是一种微型化的加速度计,利用微机电系统技术制造。其具有小型化和轻量化、低功耗、成本效益、良好的性能等优点。
微机电系统 MEMS(Micro Electro Mechanical Systems): 微机械电子系统是微电子技术的拓宽和延伸,它是将微电子技术和精密机械加工技术相互融合,并将微电子与机械融为一体的系统。
其可以分为MEMS电容式加速度计、MEMS压阻式加速度计、MEMS压电式加速度计、MEMS热板式加速度计、MEMS加热气体式加速度计等。这里就介绍一下MEMS电容式加速度计。
MEMS电容式加速度计
加速度计需要特殊的、相对较重的部件,其移动滞后于加速度计外壳的移动(参考前面提到的敏感质量块),而加速度计的外壳则结合至待测物体。所以位移换能器可用来产生加速度作用形成的电信号。
这个重的部件通常称为激振质量、惯性质量或检测质量。任何能够在强振动或线性加速度之下测量微小运动的合适的位移换能器,都能用于加速度计。
电容式加速度传感器基本都包含至少两个部分,首先是“固定”极板(即连接至外壳),另一个是附着在惯性质量上的极板,能够在外壳内自由移动。这些极板形成电容,其值是极板之间距离d的函数:
C = κ ε 0 A d \mathrm{C}=\frac{\kappa \varepsilon_0 \mathrm{~A}}{\mathrm{~d}} C= dκε0 A
其中 κ \kappa κ是介电常数。可以说此电容器的值由加速度调制。用电容式加速度计测量的最大位移很少超过20μm。因而如此小的位移需要对漂移和各种干扰进行可靠补偿。通常用差动技术实现,其中以相同结构形成一个额外的电容器。第二个电容器的值必须接近第一个的值,同时要实现180°的相移改变。于是加速度就可由两个电容器值的差来表示。
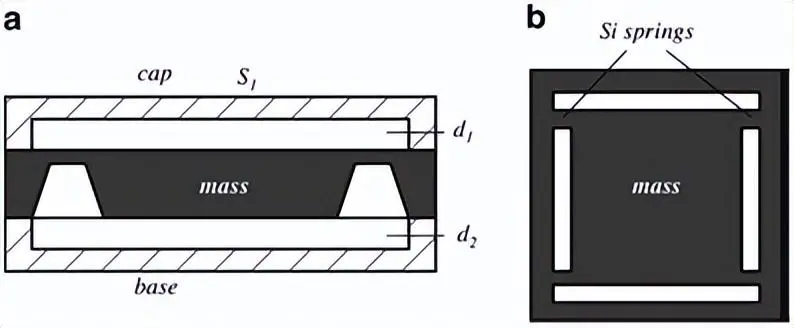
上图表示电容式加速度计的截面图,其中惯性质量夹在上盖和基座之间,质量体由四个硅弹簧支撑。上盖板和基座板与质量体分隔的距离分别为d1和d2。所有三个部件在硅片上用微机械加工制备。
其他类别加速度计
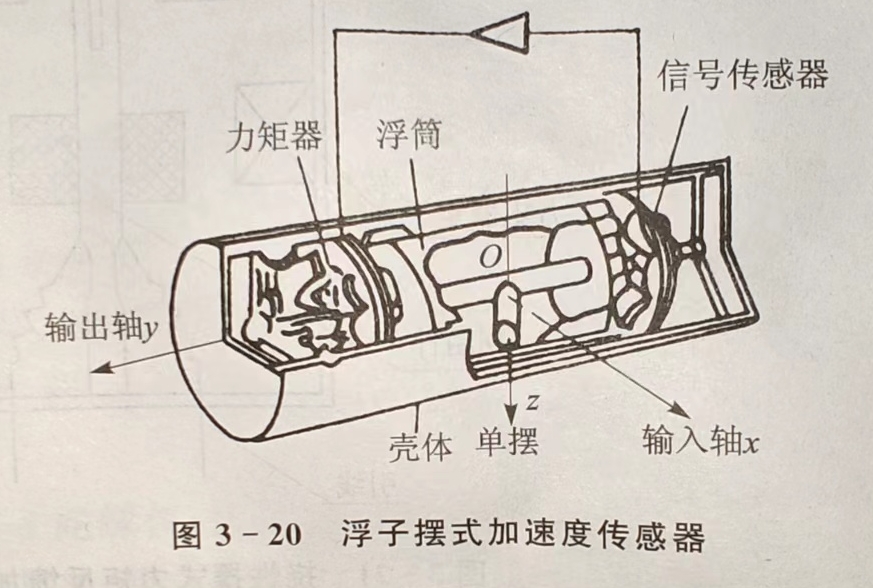
- 浮子摆式加速度传感器: 由浮子摆组合件、力矩器、信号传感器、放大器和充满粘性液体的密封壳体组成,其中浮子摆组合件由单摆、浮筒、信号传感器的转子和力矩器的转子构成。浮筒中的单摆相对于简单线加速度传感器的活动质量块,其工作原理与简单线加速度传感器相同,只是具体参数不同。
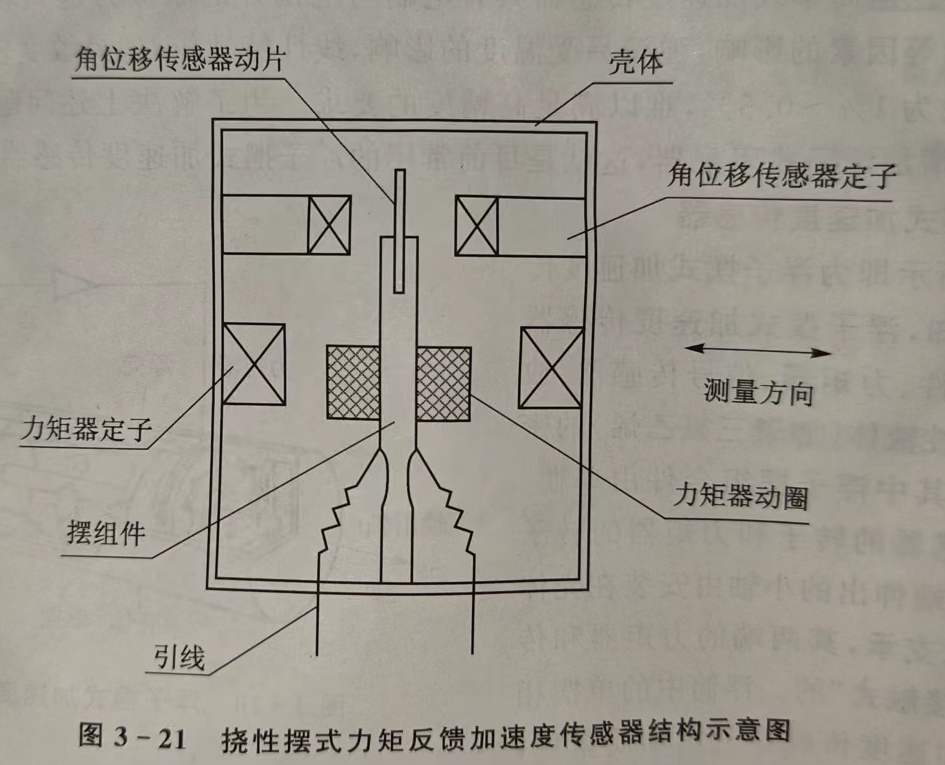
- 挠性摆式力矩反馈加速度传感器: 其由挠性支撑、摆组件、角位移传感器、力矩器及反馈电子组件(放大器和校正网络等)组成。当沿加速度输入轴具有加速度 a a a输入时,摆组件的质量 m m m将产生惯性力,该惯性力的作用方向与加速度 a a a方向相反,并对挠性轴产生惯性力矩。力矩使摆组件绕输出轴转动,产生角位移。角位移传感器将该角度位移转变为电信号,并经放大、解耦、校正,变为直流信号输出。力矩器线圈中输入相应电流,与永磁场相互作用产生电磁力,对挠性轴产生相应的恢复力矩,使摆组件最终达到平衡状态。
缺点
加速度计的缺点是信号受振动影响大,所以在无人机上使用时需要进行减震处理,在数据获取后也会进行滤波。
陀螺仪
陀螺仪的种类繁多,有MEMS陀螺、压电陀螺、激光陀螺、光纤陀螺等,不同的陀螺仪价格可以差上成千上万倍。通常小型无人机上使用的是MEMS陀螺仪,它是基于科里奥利力的工作原理,科里奥利力是对直线运动物体相对于旋转坐标系产生,因为科里奥利力正比于旋转角速度,所以可以根据科里奥利力产生的电容变化计算出相应的角速度。
按照原理,可以分为机电式陀螺仪(以经典力学为基础)、光电类陀螺仪(以近代物理学效应为基础)
- 机电式陀螺仪(以经典力学为基础)
- 转子式陀螺仪:滚珠轴承支撑陀螺、液浮陀螺、气浮陀螺、静电陀螺等
- 新型振动陀螺仪:音叉陀螺、半球谐振陀螺、微机电陀螺(MEMS)等
- 光电类陀螺仪(以光学Sagnac效应测量运载体旋转运动为基础)
- 激光陀螺、光纤陀螺、原子干涉陀螺、集成光学陀螺等
机电式: 高速旋转的机械转子,高速转子容易产生质量不平衡,容易受到加速度的影响;启动时间较长,且需要一定的预热时间;
MEMS陀螺仪是利用科里奥利力定理,将旋转物体的角速度转换成与角速度成正比的直流电压信号。
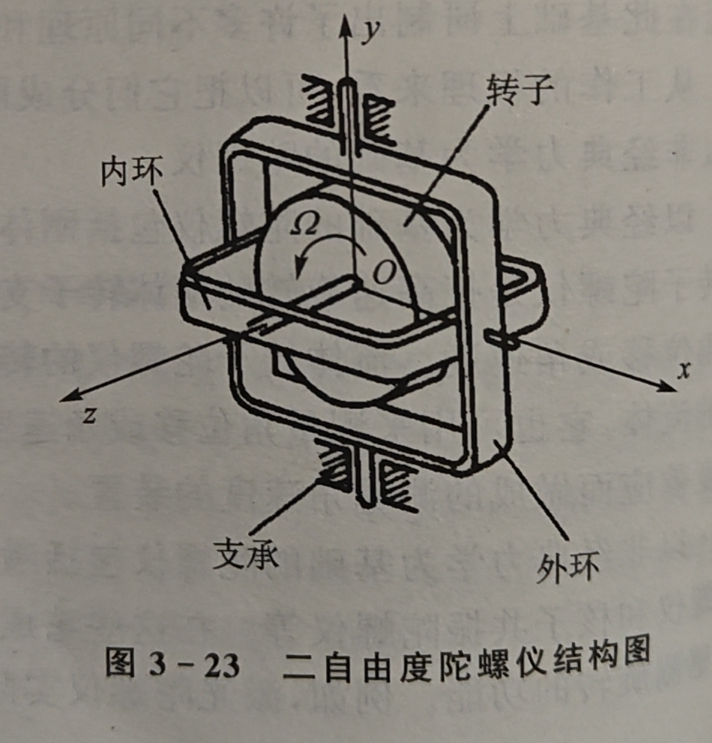
基本构成(刚体转子陀螺仪)
- 转子:常使用电机(比如同步电机、磁滞电机、三相交流电机等)驱动陀螺转子绕其自转轴高速旋转,并使其转速近似保持为常值
- 自转轴
- 万向支架(内、外环):使陀螺自转轴获得所需角转动自由度
- 力矩马达、信号传感器等
原理
物体在旋转时,其旋转轴在不受外力影响的情况下,旋转轴所指方向不变。因此可以用来测量角位移或角速度。
核心工作原理: 角动量守恒定律,指系统所受合外力矩为零时系统的角动量保持不变。假设一个陀螺不受空气阻力(合外力力矩=0),陀螺与地面的接触面无限小(矢径=0),则角动量的合力矩为0,即角动量守恒。
基本特性:
- 定轴性: 当陀螺转子以高速旋转时,在没有任何外力矩作用在陀螺仪上时,陀螺仪的自转轴在惯性空间中的指向保持稳定不变,即指向一个固定的方向;同时反抗任何改变转子轴向的力量。这种物理现象称为陀螺仪的定轴性或稳定性。
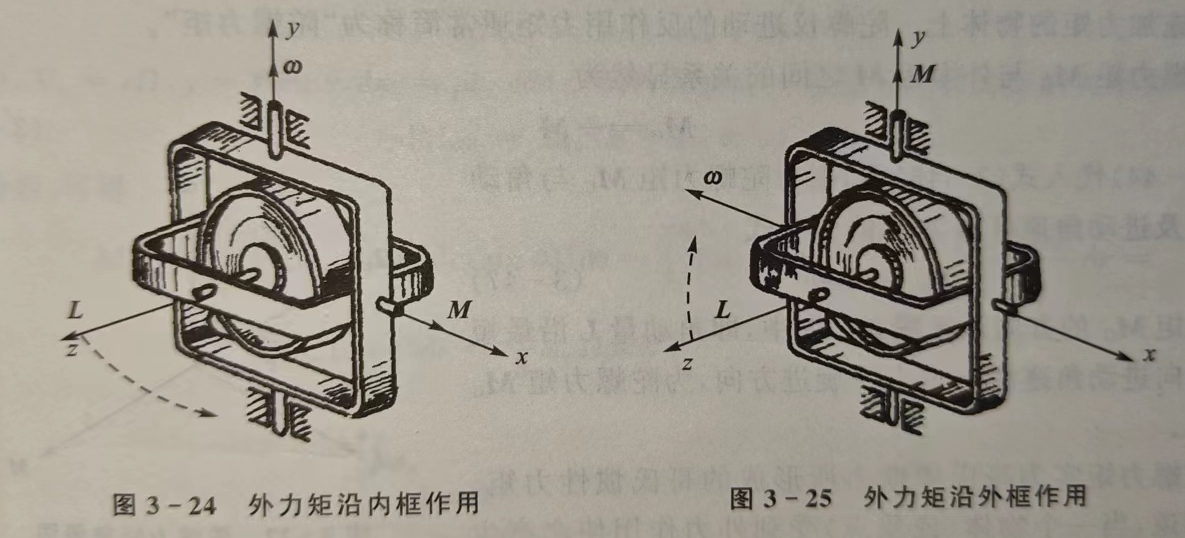
- 进动性: 当转子高速旋转时,若外力矩作用于外环轴,陀螺仪将绕内环轴转动;若外力矩作用于内环轴,陀螺仪将绕外环轴转动。其转动角速度方向与外力矩作用方向互相垂直。这种特性,叫做陀螺仪的进动性。
测量的物理量:
- 角速度:测量的物理量是偏转、倾斜时的转动角速度。
- 方向:俯仰角、偏航角、滚转角。
核心参数:
- 通用参数(传感器)
- 线性误差:传感器测量值与实际物理值之间的误差
- 分辨率:可检测到的最小物理量单位
- 采样频率:单位时间内的采样次数
- 陀螺仪重要参数
- 量程:为角速度单位(dps,degree per second)
- 灵敏度(刻度因子):最小分辨的角速度
- 灵敏度初始误差
- 灵敏度动态误差
- 非线性度:满量程的误差
- 初始零漂
- 零漂温度系数
MEMS陀螺仪原理
MEMS陀螺的基本原理是利用科里奥利力进行能量的传递,将谐振器的一种振动模式激励到另一种振动模式,后一种振动模式的振幅与输入角速度的大小成正比,通过测量振幅实现对角速度的测量。
科里奥利力:
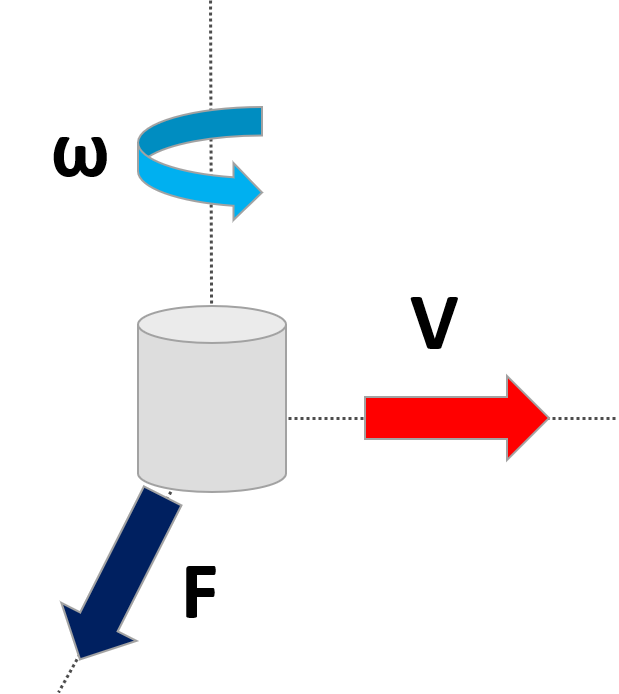
上图为科里奥利力示意图,假设一个物体以特定的速度 V V V沿着一个方向移动,如图中红色箭头所示。当一个外部角速率被施加时,如蓝色箭头所示。这个时候将产生一个力,如黑色箭头所示,这个力将导致物体发生相对于施加角速度方向的垂直位移。
工作原理:
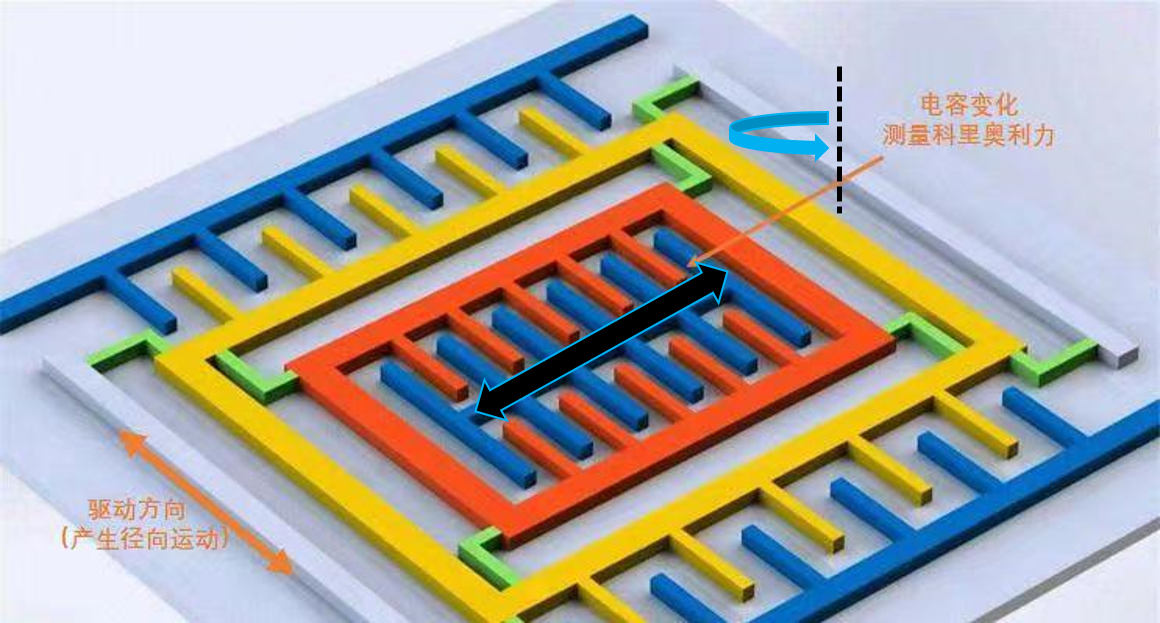
一个接近真实MEMS陀螺仪的结构如下图所示,外侧的蓝色与黄色部分别为驱动电极,它们在驱动方向施加交变电压,使内部的红色质量块以及红色的测量电极沿着驱动方向作往返运动。红色质量块两头通过有弹簧性质的绿色长条结构与基底相连,红色的短栅与内侧蓝色的短栅为电容的极板。当基底发生如下图所示的蓝色箭头旋转时,质量块在科里奥利力的作用下将产生下图黑色箭头所示垂直方向的运动。且质量块周期运动的幅值与施加的角速度成正比,通过测量质量块上的红色电极和固定在底座上蓝色电极之间的电容,便可以得到角速度的大小。
缺点
- 漂移: 陀螺仪可能存在漂移问题,即在长时间使用或暴露于恒温变化时,其测量结果可能会逐渐偏离真实值。即使没有外部干扰,长时间运行的陀螺仪也可能出现漂移。由于角速度积分得到的角度随时间漂移严重,所以单一的陀螺仪无法计算出准确的角度值,通常需要配合加速度一起使用。
- 温度敏感性: 温度变化可能影响陀螺仪的性能。温度的变化可以导致陀螺仪出现漂移或不准确的测量结果。
- 机械性能稳定性: 陀螺仪通常包含机械部件,这些部件可能受到机械磨损、震动或冲击的影响,从而影响其性能和准确性。
- 高成本: 高性能的陀螺仪通常价格昂贵,这限制了其在某些应用领域的广泛应用,尤其是对成本要求较高的消费类产品。
磁力计
磁力计正如名称所示,是利用各向异性磁致电阻或者霍尔效应来测量空间中的磁感应强度。根据洛伦兹力原理,电磁场的强度变化会产生洛伦兹力的变化,从而改变电路中的电容大小。
磁力计一般不会单独使用,通常是配合加速度计和陀螺仪一同解算姿态角的大小。另外,磁力计对于硬铁、软铁等永磁性物质都非常敏感。周围磁场的变化对磁力计的使用都会产生影响,可以说磁力计是无人机传感器中最容易受干扰的一位了。
磁力计的工作原理通常基于霍尔效应或者磁阻效应。
-
霍尔效应磁力计:
- 霍尔效应原理: 霍尔效应是指当导体(通常是半导体)通过一个磁场时,垂直于磁场和电流方向产生的电势差。当一个电流通过霍尔元件(霍尔传感器)时,该元件中的电荷载流子受到磁场力的影响,从而产生电势差。
- 工作原理: 磁力计中使用霍尔元件来感应周围的磁场。当磁场方向和强度变化时,霍尔元件中产生的电势差也会相应变化。通过测量这个电势差,磁力计可以确定磁场的强度和方向。市场上几乎90%的传感器都使用霍尔效应。
-
磁阻效应磁力计:
- 磁阻效应原理: 磁阻效应是指当磁场对磁性材料的磁性方向产生影响时,该材料的电阻发生变化。磁阻效应传感器利用这种磁阻变化来测量磁场。
- 工作原理: 磁阻效应磁力计包含磁敏感材料,当受到外部磁场的影响时,材料的电阻发生变化。通过测量电阻变化,磁力计可以得知磁场的强度和方向。
IMU惯性测量单元
通常由三轴加速度传感器和三轴陀螺仪组成。分为三轴、六轴、九轴:
- 三轴 = 3轴陀螺仪
- 六轴 = 3轴加速度计 + 3轴陀螺仪
- 九轴 = 3轴加速度计 + 3轴陀螺仪 + 3轴磁力计
如使用较多的 MPU6050 = 三轴MEMS陀螺仪 + 三轴MEMS加速度计 + 可扩展数字运动处理器DMP
相关算法
姿态融合算法
姿态融合算法是使用陀螺仪、加速度计两种传感器,并设计一种滤波算法,以分别计算在静止状态、运动状态下的姿态数据。当静止状态时,增加加速度计数据的权重;当运动状态时,增加陀螺仪数据的权重,以获得更准确的姿态数据。
相应的噪声
陀螺仪: 陀螺仪直接测量的是角速度而非角度,所以需要通过一次积分才能得到角度值。在积分的过程中若有固定的、某一个方向的数据则会在积分的过程中不断加大影响导致角度偏差。通常来说陀螺仪的温漂是比较严重的,温漂的数据既与温度相关又与时间相关,也就是说不同温度下不一样,不同上电时间下也不一样。通常的简单做法就是在上电的时候静止一段时间计算出此时的零偏,然后每次减去零偏。
加速度计: 对于加速度机同样会有零漂和尺度因子的误差,但是加速度计在静止时可直接得到角度不用积分,所以零漂的影响很小,但是尺度因子的影响较大。同样是重力加速度、各个面朝下时检测到的数值是不一样的,一般来说校准的方法有六面校准。就是各个面朝下然后记录重力的数值,计算得到尺度因子。
磁力计: 磁力计的数据误差较大,校准便显得很重要。一般可以导出数据到matlab中然后采用椭球校准的方法。
零偏(Bias): IMU传感器在完全静止状态下存在的非零输出值,属于加性误差;
尺度因子(Scale): IMU传感器自身尺度不准引起的测量误差,属于乘性误差;scale 可以看成是实际数值和传感器输出值之间的比值(电信号到模拟信号,单位不同会通过一个 scale 的转化,这个 scale 会存在误差)。
零漂: 零点漂移现象是指当放大电路的输入信号为零(即没有交流电输入)时,因受温度变化、电源电压不稳等因素影响,静态工作点发生变化,并被逐级放大和传输,导致电路输出端电压偏离原固定值而上下漂动的现象。造成零点漂移的原因有很多,任何元件参数的变化都可造成输出电压漂移,其中包括但不限于温度变化、电源电压不稳等。
姿态融合的大致描述
陀螺仪直接积分获得角度,但是会带来巨大的误差,加速度计的作用便是直接测量出俯仰角和滚转角,对积分得到的角度做一个矫正。磁力计可以看成一个指南针,可以对偏航角进行一个矫正。中间的姿态解算采用各种算法,如:互补滤波、AHRS(Madgwick和mahony)、卡尔曼滤波。
四元数与欧拉角的转换
在姿态融合解算过程中,使用四元数表示姿态,由三个实数和一个虚数组成。但一般在数据处理的时候会使用四元数,处理后再将四元数转换为欧拉角。最大的原因是使用四元数计算量小,且能避免万向节死锁的问题。
万向节死锁: 是指物体的两个旋转轴指向同一个方向。实际上,当两个旋转轴平行时,我们就说万向节锁现象发生了,换句话说,绕一个轴旋转可能会覆盖住另一个轴的旋转,从而失去一维自由度
欧拉角
首先看欧拉角:由三个角度组成,在特定坐标系下用于描述刚体的姿态。
欧拉角按旋转的坐标系分为 内旋(intrinsic rotation)和外旋(extrinsic rotation )。
按旋转轴分为 经典欧拉角(Proper Euler Angle)和泰特布莱恩角(Tait–Bryan angles) 。
经典欧拉角(Proper Euler Angle) :按(z-x-z, x-y-x, y-z-y, z-y-z, x-z-x, y-x-y)轴序列旋转,即第一个旋转轴和最后一个旋转轴相同。
泰特布莱恩角(Tait–Bryan angles) :按(x-y-z, y-z-x, z-x-y, x-z-y, z-y-x, y-x-z)轴序列旋转,即三个不同的轴 。
总计12种顺规,不同顺序的旋转产生的欧拉角是不同的。
绕固定(参考)坐标轴旋转 :假设开始两个坐标系重合,先将{B}绕{A}的X轴旋转 γ \gamma γ,然后绕{A}的Y轴旋转 β \beta β,最后绕{A}的Z轴旋转 α \alpha α,就能旋转到当前姿态。可以称其为X-Y-Z fixed angles或RPY角(Roll, Pitch, Yaw)。由于是绕固定坐标系旋转,则旋转矩阵为:
R X Y Z ( γ , β , α ) = R Z ( α ) R Y ( β ) R X ( γ ) = [ c α c β c α s β s γ − s α c γ c α s β c γ + s α s γ s α c β s α s β s γ + c α c γ s α s β c γ − c α s γ − s β c β s γ c β c γ ] R_{X Y Z}(\gamma, \beta, \alpha)=R_Z(\alpha) R_Y(\beta) R_X(\gamma)=\left[\begin{array}{ccc} c \alpha c \beta & c \alpha s \beta s \gamma-s \alpha c \gamma & c \alpha s \beta c \gamma+s \alpha s \gamma \\ s \alpha c \beta & s \alpha s \beta s \gamma+c \alpha c \gamma & s \alpha s \beta c \gamma-c \alpha s \gamma \\ -s \beta & c \beta s \gamma & c \beta c \gamma \end{array}\right] RXYZ(γ,β,α)=RZ(α)RY(β)RX(γ)= cαcβsαcβ−sβcαsβsγ−sαcγsαsβsγ+cαcγcβsγcαsβcγ+sαsγsαsβcγ−cαsγcβcγ
绕自身坐标轴旋转 :假设开始两个坐标系重合,先将{B}绕自身的Z轴旋转 α \alpha α,然后绕Y轴旋转 β \beta β,最后绕X轴旋转 γ \gamma γ,就能旋转到当前姿态。称其为Z-Y-X欧拉角,由于是绕自身坐标轴进行旋转,则旋转矩阵为:
R Z ′ Y ′ X ′ ( α , β , γ ) = R Z ( α ) R Y ( β ) R X ( γ ) = [ c α c β c α s β s γ − s α c γ c α s β c γ + s α s γ s α c β s α s β s γ + c α c γ s α s β c γ − c α s γ − s β c β s γ c β c γ ] R_{Z^{\prime} Y^{\prime} X^{\prime}}(\alpha, \beta, \gamma)=R_Z(\alpha) R_Y(\beta) R_X(\gamma)=\left[\begin{array}{ccc} c \alpha c \beta & c \alpha s \beta s \gamma-s \alpha c \gamma & c \alpha s \beta c \gamma+s \alpha s \gamma \\ s \alpha c \beta & s \alpha s \beta s \gamma+c \alpha c \gamma & s \alpha s \beta c \gamma-c \alpha s \gamma \\ -s \beta & c \beta s \gamma & c \beta c \gamma \end{array}\right] RZ′Y′X′(α,β,γ)=RZ(α)RY(β)RX(γ)= cαcβsαcβ−sβcαsβsγ−sαcγsαsβsγ+cαcγcβsγcαsβcγ+sαsγsαsβcγ−cαsγcβcγ
可以发现这两种描述方式得到的旋转矩阵是一样的,即绕固定坐标轴X-Y-Z旋转( γ \gamma γ, β \beta β, α \alpha α)和绕自身坐标轴Z-Y-X旋转( α \alpha α, β \beta β, γ \gamma γ)的最终结果一样,只是描述的方法有差别而已。
四元数
绕坐标轴的多次旋转可以等效为绕某一转轴旋转一定的角度。假设等效旋转轴方向向量为 K ⃗ = [ k x , k y , k z ] T \vec{K}=\left[k_x, k_y, k_z\right]^T K=[kx,ky,kz]T,等效旋转角为 θ \theta θ,则四元数为 q = ( w , x , y , z ) q=(w, x, y, z ) q=(w,x,y,z),其中:
x = k x ⋅ sin θ 2 y = k y ⋅ sin θ 2 z = k z ⋅ sin θ 2 w = cos θ 2 \begin{aligned} & x=k_x \cdot \sin \frac{\theta}{2} \\ & y=k_y \cdot \sin \frac{\theta}{2} \\ & z=k_z \cdot \sin \frac{\theta}{2} \\ & w=\cos \frac{\theta}{2} \end{aligned} x=kx⋅sin2θy=ky⋅sin2θz=kz⋅sin2θw=cos2θ
且有 x 2 + y 2 + z 2 + w 2 = 1 x^2+y^2+z^2+w^2=1 x2+y2+z2+w2=1
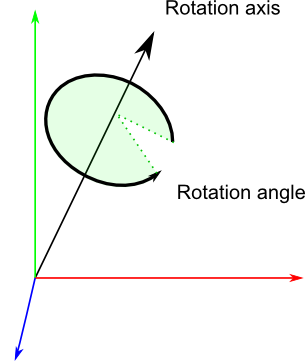
欧拉角与四元数转化
欧拉角至四元数
比如说按照旋转顺序:ZYX
旋转角. 转转轴 等效旋转轴 对应四元数 航偏角 α Z ( 0 , 0 , 1 ) Q α = cos ( α 2 ) + 0 i + 0 j + sin ( α 2 ) k 俯仰角 β Y ( 0 , 1 , 0 ) Q β = cos ( β 2 ) + 0 i + sin ( β 2 ) j + 0 k 滚转角 γ X ( 1 , 0 , 0 ) Q γ = cos ( γ 2 ) + sin ( γ 2 ) i + 0 j + 0 k \begin{array}{|c|c|c|c|} \hline \text { 旋转角. } & \text { 转转轴 } &\text { 等效旋转轴 } & \text { 对应四元数 } \\ \hline \text { 航偏角 } \alpha & \mathrm{Z} & (0,0,1) & \mathrm{Q}_{\alpha}=\cos \left(\frac{\alpha}{2}\right)+0 i+0 j+\sin \left(\frac{\alpha}{2}\right) k \\ \hline \text { 俯仰角 } \beta & \mathrm{Y} & (0,1,0) & \mathrm{Q}_\beta=\cos \left(\frac{\beta}{2}\right)+0 i+\sin \left(\frac{\beta}{2}\right) j+0 k \\ \hline \text { 滚转角 } \gamma & \mathrm{X} & (1,0,0) & \mathrm{Q}_{\gamma}=\cos \left(\frac{\gamma}{2}\right)+\sin \left(\frac{\gamma}{2}\right) i+0 j+0 k \\ \hline \end{array} 旋转角. 航偏角 α 俯仰角 β 滚转角 γ 转转轴 ZYX 等效旋转轴 (0,0,1)(0,1,0)(1,0,0) 对应四元数 Qα=cos(2α)+0i+0j+sin(2α)kQβ=cos(2β)+0i+sin(2β)j+0kQγ=cos(2γ)+sin(2γ)i+0j+0k
接下来可以得到式子:
q = [ cos γ 2 0 0 sin γ 2 ] [ cos β 2 0 sin β 2 0 ] [ cos α 2 sin α 2 0 0 ] = [ cos α 2 cos β 2 cos γ 2 + sin α 2 sin β 2 sin γ 2 sin α 2 cos β 2 cos γ 2 − cos α 2 sin β 2 sin γ 2 cos α 2 sin β 2 cos γ 2 + sin α 2 cos β 2 sin γ 2 cos α 2 cos β 2 sin γ 2 − sin α 2 sin β 2 cos γ 2 ] q=\left[\begin{array}{c} \cos \frac{\gamma}{2} \\ 0 \\ 0 \\ \sin \frac{\gamma}{2} \end{array}\right]\left[\begin{array}{c} \cos \frac{\beta}{2} \\ 0 \\ \sin \frac{\beta}{2} \\ 0 \end{array}\right]\left[\begin{array}{c} \cos \frac{\alpha}{2} \\ \sin \frac{\alpha}{2} \\ 0 \\ 0 \end{array}\right]=\left[\begin{array}{c} \cos \frac{\alpha}{2} \cos \frac{\beta}{2} \cos \frac{\gamma}{2}+\sin \frac{\alpha}{2} \sin \frac{\beta}{2} \sin \frac{\gamma}{2} \\ \sin \frac{\alpha}{2} \cos \frac{\beta}{2} \cos \frac{\gamma}{2}-\cos \frac{\alpha}{2} \sin \frac{\beta}{2} \sin \frac{\gamma}{2} \\ \cos \frac{\alpha}{2} \sin \frac{\beta}{2} \cos \frac{\gamma}{2}+\sin \frac{\alpha}{2} \cos \frac{\beta}{2} \sin \frac{\gamma}{2} \\ \cos \frac{\alpha}{2} \cos \frac{\beta}{2} \sin \frac{\gamma}{2}-\sin \frac{\alpha}{2} \sin \frac{\beta}{2} \cos \frac{\gamma}{2} \end{array}\right] q= cos2γ00sin2γ cos2β0sin2β0 cos2αsin2α00 = cos2αcos2βcos2γ+sin2αsin2βsin2γsin2αcos2βcos2γ−cos2αsin2βsin2γcos2αsin2βcos2γ+sin2αcos2βsin2γcos2αcos2βsin2γ−sin2αsin2βcos2γ
PS: 这里不是矩阵的乘法,而是四元数的乘法。
四元数乘法: 定义两个四元数:
p = a + u ⃗ = a + b i + c j + d k q = t + v ⃗ = t + x i + y j + z k \begin{aligned} & p=a+\vec{u}=a+b i+c j+d k \\ & q=t+\vec{v}=t+x i+y j+z k \end{aligned} p=a+u=a+bi+cj+dkq=t+v=t+xi+yj+zk
则:
p q = a t − u ⃗ ⋅ v ⃗ + a v ⃗ + t u ⃗ + u ⃗ × v ⃗ p q = ( a t − b x − c y − d z ) + ( a x + b t + c z − d y ) i + ( a y − b z + c t + d x ) j + ( a z + d t − c x + b y ) k \begin{gathered} p q=a t-\vec{u} \cdot \vec{v}+a \vec{v}+t \vec{u}+\vec{u} \times \vec{v} \\ p q=(a t-b x-c y-d z)+(a x+b t+c z-d y) i+(a y-b z+c t+d x) j+(a z+d t-c x+b y) k \end{gathered} pq=at−u⋅v+av+tu+u×vpq=(at−bx−cy−dz)+(ax+bt+cz−dy)i+(ay−bz+ct+dx)j+(az+dt−cx+by)k
四元数至欧拉角
首先得到四元数至旋转矩阵的转换公式:
R = [ 1 − 2 y 2 − 2 z 2 2 ( x y − z w ) 2 ( x z + y w ) 2 ( x y + z w ) 1 − 2 x 2 − 2 z 2 2 ( y z − x w ) 2 ( x z − y w ) 2 ( y z + x w ) 1 − 2 x 2 − 2 y 2 ] R=\left[\begin{array}{ccc} 1-2 y^2-2 z^2 & 2(x y-z w) & 2(x z+y w) \\ 2(x y+z w) & 1-2 x^2-2 z^2 & 2(y z-x w) \\ 2(x z-y w) & 2(y z+x w) & 1-2 x^2-2 y^2 \end{array}\right] R= 1−2y2−2z22(xy+zw)2(xz−yw)2(xy−zw)1−2x2−2z22(yz+xw)2(xz+yw)2(yz−xw)1−2x2−2y2
PS: 通过3D旋转公式得到
将式
R X Y Z ( γ , β , α ) = R Z ( α ) R Y ( β ) R X ( γ ) = [ c α c β c α s β s γ − s α c γ c α s β c γ + s α s γ s α c β s α s β s γ + c α c γ s α s β c γ − c α s γ − s β c β s γ c β c γ ] R_{X Y Z}(\gamma, \beta, \alpha)=R_Z(\alpha) R_Y(\beta) R_X(\gamma)=\left[\begin{array}{ccc} c \alpha c \beta & c \alpha s \beta s \gamma-s \alpha c \gamma & c \alpha s \beta c \gamma+s \alpha s \gamma \\ s \alpha c \beta & s \alpha s \beta s \gamma+c \alpha c \gamma & s \alpha s \beta c \gamma-c \alpha s \gamma \\ -s \beta & c \beta s \gamma & c \beta c \gamma \end{array}\right] RXYZ(γ,β,α)=RZ(α)RY(β)RX(γ)= cαcβsαcβ−sβcαsβsγ−sαcγsαsβsγ+cαcγcβsγcαsβcγ+sαsγsαsβcγ−cαsγcβcγ
与式
R = [ 1 − 2 y 2 − 2 z 2 2 ( x y − z w ) 2 ( x z + y w ) 2 ( x y + z w ) 1 − 2 x 2 − 2 z 2 2 ( y z − x w ) 2 ( x z − y w ) 2 ( y z + x w ) 1 − 2 x 2 − 2 y 2 ] R=\left[\begin{array}{ccc} 1-2 y^2-2 z^2 & 2(x y-z w) & 2(x z+y w) \\ 2(x y+z w) & 1-2 x^2-2 z^2 & 2(y z-x w) \\ 2(x z-y w) & 2(y z+x w) & 1-2 x^2-2 y^2 \end{array}\right] R= 1−2y2−2z22(xy+zw)2(xz−yw)2(xy−zw)1−2x2−2z22(yz+xw)2(xz+yw)2(yz−xw)1−2x2−2y2
两个矩阵一一对应,可以得到
tan α = 2 ( x y − w z ) w 2 + x 2 − y 2 − z 2 sin β = − 2 ( w y + x z ) tan γ = 2 ( y z − w x ) w 2 − x 2 − y 2 + z 2 \begin{aligned} & \tan \alpha=\frac{2\left(x y-w z\right)}{w^2+x^2-y^2-z^2} \\ & \sin \beta=-2\left(w y+x z\right) \\ & \tan \gamma=\frac{2\left(y z-w x\right)}{w^2-x^2-y^2+z^2} \end{aligned} tanα=w2+x2−y2−z22(xy−wz)sinβ=−2(wy+xz)tanγ=w2−x2−y2+z22(yz−wx)
很多地方四元数用 q = ( q 0 , q 1 , q 2 , q 3 ) q=\left(q_0, q_1, q_2, q_3\right) q=(q0,q1,q2,q3)(或 q = ( w , x , y , z ) q=(w, x, y, z) q=(w,x,y,z))表示,则表达式为
tan α = 2 ( q 1 q 2 − q 0 q 3 ) q 0 2 + q 1 2 − q 2 2 − q 3 2 sin β = − 2 ( q 0 q 2 + q 1 q 3 ) tan γ = 2 ( q 2 q 3 − q 0 q 1 ) q 0 2 − q 1 2 − q 2 2 + q 3 2 \begin{aligned} & \tan \alpha=\frac{2\left(q_1 q_2-q_0 q_3\right)}{q_0^2+q_1^2-q_2^2-q_3^2} \\ & \sin \beta=-2\left(q_0 q_2+q_1 q_3\right) \\ & \tan \gamma=\frac{2\left(q_2 q_3-q_0 q_1\right)}{q_0^2-q_1^2-q_2^2+q_3^2} \end{aligned} tanα=q02+q12−q22−q322(q1q2−q0q3)sinβ=−2(q0q2+q1q3)tanγ=q02−q12−q22+q322(q2q3−q0q1)
进一步得到
航偏角:
α
=
arctan
(
2
(
q
1
q
2
−
q
0
q
3
)
q
0
2
+
q
1
2
−
q
2
2
−
q
3
2
)
\alpha=\arctan \left(\frac{2\left(q_1 q_2-q_0 q_3\right)}{q_0^2+q_1{ }^2-q_2^2-q_3{ }^2}\right)
α=arctan(q02+q12−q22−q322(q1q2−q0q3)).
俯仰角:
β
=
arcsin
(
−
2
(
q
0
q
2
+
q
1
q
3
)
)
\beta=\arcsin \left(-2\left(q_0 q_2+q_1 q_3\right)\right)
β=arcsin(−2(q0q2+q1q3))
滚转角:
γ
=
arctan
(
2
(
q
2
q
3
−
q
0
q
1
)
q
0
2
−
q
1
2
−
q
2
2
+
q
3
2
)
\gamma=\arctan \left(\frac{2\left(q_2 q_3-q_0 q_1\right)}{q_0{ }^2-q_1{ }^2-q_2{ }^2+q_3{ }^2}\right)
γ=arctan(q02−q12−q22+q322(q2q3−q0q1))
GPS
使用GPS确定无人机的三维坐标。
有了GPS后,无人机能够悬停飞行(定点),飞手操作的复杂性大大降低,同时,为了能够执行一些航迹飞行任务,定位信息也是必要的。
首先,宇宙里的卫星会不停的向地面的GPS接收机(常用的GPS模块)广播当前的位置信息,包括该数据包的时间戳,当GPS模块接收到这些信息后,用当前时间减去时间戳的时间,就得到空中传输的时间,乘上传输速度,就得到卫星与GPS模块的距离。
理论来讲,为了确定GPS模块的坐标位置(NEH),3个参数,那只需要3颗卫星与GPS模块的距离就可以计算出来。
但是因为对时间差的要求特别高,由于GPS模块的时钟一般是石英钟,所以认为它的时钟时间与卫星的时间有同步误差,所以加上这个误差作为参数,这样就有4个参数待定,所以一般 至少需要4颗卫星进行观测 。
气压计
气压计运作的原理,就是利用大气压力换算出高度。 气压计也是容易受外界干扰的一个传感器,当温度发生变化时,气压也会发生变化,另外,无人机上旋翼工作产生的气流通常也会影响气压计的测量。所以,如果安装了超声波或者激光测距传感器等相对高度传感器,我们可以使用超声波/激光测距仪+GPS高度的方式替代气压计的方案。
超声波传感器
超声波是一种超出人耳听觉频率上线的声波,由于具有良好的方向性和强大的穿透性,被广泛用于测距和测速。超声波的信号由超声波传感器发出,被物体反射后再经由另一台超声波传感器接收。所以到物体的距离就是声波的传播速度与时间间隔乘积的一半。
超声波传感器的价格普遍比较便宜,但是由于声波传输速度慢,所以超声波传感器的数据更新频率相对较低,同时测量范围小,这些都是超声波传感器的缺点。
激光测距传感器
激光测距传感器的原理基本跟超声波传感器一致,只不过发射的信号不同,激光测距传感器发射的是激光源,其传播速度时光速,所以,在信号频率上比超声波传感器要高很多,价格上也比超声波传感器要高一个数量级。
视觉传感器
视觉传感器指的是使用摄像头来获取图像信息,然后根据图像信息确定目标或者无人机相对于目标的位置和速度等状态信息。视觉传感器更重要的是后期处理算法,尤其是最近几年深度学习算法的发展给视觉传感器在无人机上的应用带来了新的生机,最近很多关于无人机的研究都是基于视觉进行的,比如基于视觉的目标跟踪,避障、定位等。
空速计
空速计一般是固定翼无人机上使用的较多,因为固定翼飞行器的各类状态都跟空速息息相关,比如说升力,比如说失速速度。空速计的测量原理是通过测量气流的总压和静压从而根据伯努利原理确定气流的动压,再计算出空速。







 本文围绕无人机常用传感器展开,介绍了加速度计、陀螺仪、磁力计等多种传感器的原理、优缺点。还阐述了IMU惯性测量单元及相关姿态融合算法,以及四元数与欧拉角的转换。此外,对GPS、气压计等传感器的作用和特点也进行了说明,为无人机导航提供支持。
本文围绕无人机常用传感器展开,介绍了加速度计、陀螺仪、磁力计等多种传感器的原理、优缺点。还阐述了IMU惯性测量单元及相关姿态融合算法,以及四元数与欧拉角的转换。此外,对GPS、气压计等传感器的作用和特点也进行了说明,为无人机导航提供支持。
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








