一、开篇
还是没能进入到源码部分研究,对姿态解算过程太过于模糊,所以主要开始研究一下关于姿态解算的过程和实现,本篇博文主要是以mahony的算法为基础理解姿态解算的过程,主要参考的论文就是William Premerlani and Paul Bizard的关于DCM的一篇经典论文《Direction Cosine Matrix IMU_Theory》,一定要搞透这篇论文,没看过它都不敢称自己研究过飞控算法;然后接下来还有madgwick和mahony的论文需要研究,看英文的比较费时间,但是还是得慢慢的啃啊~~~
然后就是结合国内的一本很不错的书籍《捷联惯性导航技术》,不需要细看,只需要了解其中关于姿态解算部分的即可。国内的课本嘛,大家都懂的,恨不得手把手的教你了。国外的论文就不一样了,继续啃吧。
二、版权声明
博主:summer
声明:喝水不忘挖井人,转载请注明出处。
原文地址:http://blog.csdn.net/qq_21842557
联系方式:dxl0725@126.com
技术交流QQ:1073811738
三、实验平台
Software Version:ArduCopter(Ver_3.3)
Hardware Version:pixhawk
IDE:eclipse Juno (Windows)
四、基本知识1、 陀螺仪和加速计(特性分析)
1)陀螺仪
Gyro sensitivity、 operating range、offset、drift、calibrationandsaturation must be taken into account in the implementation of DCM。
灵敏度
测量角速度,具有高动态特性,它是一个间接测量角度的器件其中一个关键参数就是gyro sensitivity(其单位是millivolts per degree persecond,把转速转换到电压值),测量范围越小气灵敏度越好。也就是说测量的是角度的导数,即角速度,要将角速度对时间积分才能得到角度。陀螺仪就是内部有一个陀螺,它的轴由于陀螺效应始终与初始方向平行,这样就可以通过与初始方向的偏差计算出旋转方向和角度。
偏移
偏移就是在陀螺没有转动的时候却又输出,这个输出量的大小和供电电压以及温度有关,该偏移可以在陀螺仪上电时通过一小段时间的测量来修正。
漂移
它是由于在时间的积累下偏移和噪声相互影响的结果,例如有一个偏置(offset)0.1dps加在上面,于是测量出来是0.1dps,积分一秒之后,得到的角度是0.1度,1分钟之后是6度,还能忍受,一小时之后是360度,转了一圈,也就是说,陀螺仪在短时间内有很大的参考价值。
白噪声
电信号的测量中,一定会带有白噪声,陀螺仪数据的测量也不例外。所以获得的陀螺仪数据中也会带有白噪声,而且这种白噪声会随着积分而累加。
积分误差
对陀螺仪角速度的积分是离散的,长时间的积分会出现漂移的情况。所以要考虑积分误差的问题。
溢出
就是转速超过了其测量的最大转速范围。关于这个问题的解决办法,在DCM IMU:Theory中给出来三种解决办法,不写了。
2)加速度计
加速度计的低频特性好,可以测量低速的静态加速度。在无人机上就是对重力加速度g的测量和分析。当把加速度计拿在手上随意转动时,看的是重力加速度在三个轴上的分量值。加速度计在自由落体时,其输出为0。为什么会这样呢?这里涉及到加速度计的设计原理:加速度计测量加速度是通过比力来测量(比力方程,秦永元的书中有介绍),而不是通过加速度。加速度计仅仅测量的是重力加速度,而重力加速度与刚才所说的R坐标系(EarthFrame)是固连的,通过这种关系,可以得到加速度计所在平面与地面的角度关系。
加速度计仅仅测量的是重力加速度,3轴加速度计输出重力加速度在加速度计所在机体坐标系3个轴上的分量大小。重力加速度的方向和大小是固定的。通过这种关系,可以得到加速度计所在平面与地面的角度关系。加速度计若是绕着重力加速度的轴转动,则测量值不会改变,也就是说加速度计无法感知这种水平旋转。
机体好似一条船,姿态就是航向(船头的方位),重力是灯塔,陀螺(角速度积分)是舵手,加速度计是瞭望手。舵手负责估计和把稳航向,他相信自己,本来船向北开的,就一定会一直往北开,觉得转了90度弯,那就会往东开。当然如果舵手很牛逼,也许能估计很准确,维持很长时间。不过只信任舵手,肯定会迷路,所以一般都有瞭望手来观察误差。
瞭望手根据地图灯塔方位和船的当前航向,算出灯塔理论上应该在船的X方位。然而看到实际灯塔在船的Y方位,那肯定船的当前航向有偏差了,偏差就是ERR=X-Y。舵手收到瞭望手给的ERR报告,觉得可靠,那就听个90%ERR,觉得天气不好、地图误差大,那就听个10%ERR,根据这个来纠正估算航向。
3)磁传感器
可以测量磁场,在没有其他磁场的情况下,仅仅测量的是地球的磁场,而地磁也是和R坐标系固连的,通过这种关系,可以得到平面A和地平面的关系。(平面A:和磁场方向垂直的平面),同样的,若是沿着磁场方向的轴旋转,测量值不会改变,无法感知这种旋转。
综合考虑,加速度计和磁传感器都是极易受外部干扰的传感器,都只能得到2维的角度关系,但是测量值随时间的变化相对较小,结合加速度计和磁传感器可以得到3维的角度关系。陀螺仪可以积分得到三维的角度关系,动态性能好,受外部干扰小,但测量值随时间变化比较大。可以看出,它们优缺点互补,结合起来才能有好的效果。
4)关于数据融合
现在有了三个传感器,都能在一定程度上测量角度关系,但是究竟相信谁?根据刚才的分析,应该是在短时间内更加相信陀螺仪,隔三差五的问问加速度计和磁传感器,角度飘了多少了?有一点必须非常明确,陀螺仪才是主角,加速度计和磁传感器仅仅是跑龙套的。其实加速度计无法对航向角进行修正,修正航向角需要磁力计。
参考crazypony的分析:http://www.crazepony.com/wiki/mpu6050.html和《DCM IMU:Theory》五、正文
1、首先就是基于mahony算法的AHRS姿态解算的一套源码,理论基础是DCM IMU:Theory,很有参考价值。先自己分析一下,看看每一行具体是做什么的,是如何实现姿态解算和修正的。然后会给出相应的分析
- /*
- *AHRS
- */
- // AHRS.c
- // Quaternion implementation of the 'DCM filter' [Mayhony et al]. Incorporates the magnetic distortion
- // compensation algorithms from my filter [Madgwick] which eliminatesthe need for a reference
- // direction of flux (bx bz) to be predefined and limits the effect ofmagnetic distortions to yaw
- // axis only.
- // User must define 'halfT' as the (sample period / 2), and the filtergains 'Kp' and 'Ki'.
- // Global variables 'q0', 'q1', 'q2', 'q3' are the quaternion elementsrepresenting the estimated
- // orientation. See my report foran overview of the use of quaternions in this application.
- // User must call 'AHRSupdate()' every sample period and parsecalibrated gyroscope ('gx', 'gy', 'gz'),
- // accelerometer ('ax', 'ay', 'ay') and magnetometer ('mx', 'my', 'mz')data. Gyroscope units are
- // radians/second, accelerometer and magnetometer units are irrelevantas the vector is normalised.
- #include "stm32f10x.h"
- #include "AHRS.h"
- #include "Positioning.h"
- #include <math.h>
- #include <stdio.h>
- /* Private define------------------------------------------------------------*/
- #define Kp 2.0f // proportional gain governs rate of convergence toaccelerometer/magnetometer
- #define Ki 0.005f // integral gain governs rate of convergenceof gyroscope biases
- #define halfT 0.0025f // half the sample period
- #define ACCEL_1G 1000 //theacceleration of gravity is: 1000 mg
- /* Private variables---------------------------------------------------------*/
- static float q0 = 1, q1 = 0, q2 = 0, q3 = 0; // quaternion elements representing theestimated orientation
- static float exInt = 0, eyInt = 0, ezInt = 0; // scaled integral error
- /* Public variables----------------------------------------------------------*/
- EulerAngle_Type EulerAngle; //unit: radian
- u8InitEulerAngle_Finished = 0;
- float Magnetoresistor_mGauss_X = 0, Magnetoresistor_mGauss_Y = 0,Magnetoresistor_mGauss_Z = 0;//unit: milli-Gauss
- float Accelerate_mg_X, Accelerate_mg_Y, Accelerate_mg_Z;//unit: mg
- float AngularRate_dps_X, AngularRate_dps_Y, AngularRate_dps_Z;//unit:dps: degree per second
- int16_t Magnetoresistor_X, Magnetoresistor_Y, Magnetoresistor_Z;
- uint16_t Accelerate_X = 0, Accelerate_Y = 0, Accelerate_Z = 0;
- uint16_t AngularRate_X = 0, AngularRate_Y = 0, AngularRate_Z = 0;
- u8 Quaternion_Calibration_ok = 0;
- /* Private macro-------------------------------------------------------------*/
- /* Private typedef-----------------------------------------------------------*/
- /* Private function prototypes -----------------------------------------------*/
- /******************************************************************************
- *Function Name : AHRSupdate
- *Description : None
- *Input : None
- *Output : None
- *Return : None
- *******************************************************************************
- void AHRSupdate(float gx, float gy, float gz, float ax, float ay, floataz, float mx, float my, float mz) {
- float norm;
- float hx, hy, hz, bx, bz;
- float vx, vy, vz, wx, wy, wz;
- float ex, ey, ez;
- // auxiliary variables to reduce number of repeated operations
- float q0q0 = q0*q0;
- float q0q1 = q0*q1;
- float q0q2 = q0*q2;
- float q0q3 = q0*q3;
- float q1q1 = q1*q1;
- float q1q2 = q1*q2;
- float q1q3 = q1*q3;
- float q2q2 = q2*q2;
- float q2q3 = q2*q3;
- float q3q3 = q3*q3;
- // normalise the measurements
- norm = sqrt(ax*ax + ay*ay + az*az);
- ax = ax / norm;
- ay = ay / norm;
- az = az / norm;
- norm = sqrt(mx*mx + my*my + mz*mz);
- mx = mx / norm;
- my = my / norm;
- mz = mz / norm;
- // compute reference direction of magnetic field
- hx = 2*mx*(0.5 - q2q2 - q3q3) + 2*my*(q1q2 - q0q3) + 2*mz*(q1q3 + q0q2);
- hy = 2*mx*(q1q2 + q0q3) + 2*my*(0.5 - q1q1 - q3q3) + 2*mz*(q2q3 - q0q1);
- hz = 2*mx*(q1q3 - q0q2) + 2*my*(q2q3 + q0q1) + 2*mz*(0.5 - q1q1 -q2q2);
- bx = sqrt((hx*hx) + (hy*hy));
- bz = hz;
- // estimated direction of gravity and magnetic field (v and w)
- vx = 2*(q1q3 - q0q2);
- vy = 2*(q0q1 + q2q3);
- vz = q0q0 - q1q1 - q2q2 + q3q3;
- wx = 2*bx*(0.5 - q2q2 - q3q3) + 2*bz*(q1q3 - q0q2);
- wy = 2*bx*(q1q2 - q0q3) + 2*bz*(q0q1 + q2q3);
- wz = 2*bx*(q0q2 + q1q3) + 2*bz*(0.5 - q1q1 - q2q2);
- // error is sum ofcross product between reference direction of fields and directionmeasured by sensors
- ex = (ay*vz - az*vy) + (my*wz - mz*wy);
- ey = (az*vx - ax*vz) + (mz*wx - mx*wz);
- ez = (ax*vy - ay*vx) + (mx*wy - my*wx);
- // integral error scaled integral gain
- exInt = exInt + ex*Ki* (1.0f / sampleFreq);
- eyInt = eyInt + ey*Ki* (1.0f / sampleFreq);
- ezInt = ezInt + ez*Ki* (1.0f / sampleFreq);
- // adjusted gyroscope measurements
- gx = gx + Kp*ex + exInt;
- gy = gy + Kp*ey + eyInt;
- gz = gz + Kp*ez + ezInt;
- // integrate quaternion rate and normalize
- q0 = q0 + (-q1*gx - q2*gy - q3*gz)*halfT;
- q1 = q1 + (q0*gx + q2*gz - q3*gy)*halfT;
- q2 = q2 + (q0*gy - q1*gz + q3*gx)*halfT;
- q3 = q3 + (q0*gz + q1*gy - q2*gx)*halfT;
- // normalise quaternion
- norm = sqrt(q0*q0 + q1*q1 + q2*q2 + q3*q3);
- q0 = q0 / norm;
- q1 = q1 / norm;
- q2 = q2 / norm;
- q3 = q3 / norm;
- }
先给一个简要的代码注释分析。
- //陀螺仪、加速度计、磁力计数据融合
- void AHRSupdate(float gx, float gy, float gz, float ax, float ay, float az, float mx, float my, float mz) {
- float norm;
- float hx, hy, hz, bx, bz;
- float vx, vy, vz, wx, wy, wz; //v*当前姿态计算得来的重力在三轴上的分量
- float ex, ey, ez;
- // auxiliary variables to reduce number of repeated operations
- float q0q0 = q0*q0;
- float q0q1 = q0*q1;
- float q0q2 = q0*q2;
- float q0q3 = q0*q3;
- float q1q1 = q1*q1;
- float q1q2 = q1*q2;
- float q1q3 = q1*q3;
- float q2q2 = q2*q2;
- float q2q3 = q2*q3;
- float q3q3 = q3*q3;
- // normalise the measurements
- norm = sqrt(ax*ax + ay*ay + az*az);
- ax = ax / norm;
- ay = ay / norm;
- az = az / norm;
- norm = sqrt(mx*mx + my*my + mz*mz);
- mx = mx / norm;
- my = my / norm;
- mz = mz / norm;
- // compute reference direction of magnetic field
- hx = 2*mx*(0.5 - q2q2 - q3q3) + 2*my*(q1q2 - q0q3) + 2*mz*(q1q3 + q0q2);
- hy = 2*mx*(q1q2 + q0q3) + 2*my*(0.5 - q1q1 - q3q3) + 2*mz*(q2q3 - q0q1);
- hz = 2*mx*(q1q3 - q0q2) + 2*my*(q2q3 + q0q1) + 2*mz*(0.5 - q1q1 - q2q2);
- bx = sqrt((hx*hx) + (hy*hy));
- bz = hz;
- // estimated direction of gravity and magnetic field (v and w)
- //参考坐标n系转化到载体坐标b系的用四元数表示的方向余弦矩阵第三列即是。
- //处理后的重力分量
- vx = 2*(q1q3 - q0q2);
- vy = 2*(q0q1 + q2q3);
- vz = q0q0 - q1q1 - q2q2 + q3q3;
- //处理后的mag,反向使用DCM得到
- wx = 2*bx*(0.5 - q2q2 - q3q3) + 2*bz*(q1q3 - q0q2);
- wy = 2*bx*(q1q2 - q0q3) + 2*bz*(q0q1 + q2q3);
- wz = 2*bx*(q0q2 + q1q3) + 2*bz*(0.5 - q1q1 - q2q2);
- // error is sum of cross product between reference direction of fields and direction measured by sensors 体现在加速计补偿和磁力计补偿,因为仅仅依靠加速计补偿没法修正Z轴的变差,所以还需要通过磁力计来修正Z轴。(公式28)。《四元数解算姿态完全解析及资料汇总》的作者把这部分理解错了,不是什么叉积的差,而叉积的计算就是这样的。计算方法是公式10。
- ex = (ay*vz - az*vy) + (my*wz - mz*wy);
- ey = (az*vx - ax*vz) + (mz*wx - mx*wz);
- ez = (ax*vy - ay*vx) + (mx*wy - my*wx);
- // integral error scaled integral gain
- exInt = exInt + ex*Ki* (1.0f / sampleFreq);
- eyInt = eyInt + ey*Ki* (1.0f / sampleFreq);
- ezInt = ezInt + ez*Ki* (1.0f / sampleFreq);
- // adjusted gyroscope measurements
- //将误差PI后补偿到陀螺仪,即补偿零点漂移。通过调节Kp、Ki两个参数,可以控制加速度计修正陀螺仪积分姿态的速度。(公式16和公式29)
- gx = gx + Kp*ex + exInt;
- gy = gy + Kp*ey + eyInt;
- gz = gz + Kp*ez + ezInt;
- // integrate quaternion rate and normalize
- //一阶龙格库塔法更新四元数
- q0 = q0 + (-q1*gx - q2*gy - q3*gz)*halfT;
- q1 = q1 + (q0*gx + q2*gz - q3*gy)*halfT;
- q2 = q2 + (q0*gy - q1*gz + q3*gx)*halfT;
- q3 = q3 + (q0*gz + q1*gy - q2*gx)*halfT;
- // normalise quaternion
- norm = sqrt(q0*q0 + q1*q1 + q2*q2 + q3*q3);
- q0 = q0 / norm;
- q1 = q1 / norm;
- q2 = q2 / norm;
- q3 = q3 / norm;
- }
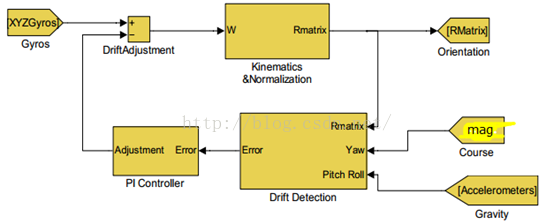
1)无人机控制中,主要就是姿态解算和姿态控制部分,该部分主要介绍姿态解算,下面是来一张比较好理解的框图。


由上面两幅图很容易理解整个控制和姿态解算了吧,在第四部分也介绍了关于陀螺仪、加速计、磁力计它们的作用,所以不再单独介绍了。不理解的往上翻翻再看看吧。
2)在姿态解算过程中,到底用什么表示无人机的姿态呢?姿态表示的方法有很多种,比如欧拉角、四元数、DCM,各有的各的优势,比较常用的就是四元数,方便计算。上面的姿态解算算法也是基于四元数的。下面介绍一个它们三个的优缺点。
姿态解算方法的比较:
| 算法 | 优点 | 缺点 | PS |
| 欧拉角法(3参数) | 1、 通过欧拉角微分方程直接解算出pitch、roll、yaw 2、 概念直观,易于理解 3、 解算结果永远是正交的,无需再次正交化处理 | 1、 方程中有三角函数的运算,接超越函数有一定的困难 2、 当俯仰角接近90°时出现退化现象 | 1、 适应于水平姿态角变化不大的情况 2、 不适用于全姿态运载体 |
| 方向余弦法(9参数) | 1、 对姿态矩阵微分方程的求解,避免了欧拉角法中出现的退化现象 2、 可以全姿态运行 | 1、参数量过多,计算量大,实时性不好 | 很少在工程中使用 |
| 四元数法(4参数) | 1、 直接求解四元数微分方程 2、 只需要求解四个参数,计算量小 3、算法简单,易于操作 | 漂移比较严重 | 可以在实现过程中修正漂移,应用比较广泛 |
首先,东北天坐标系是n系(地理坐标系,参考坐标系),载体坐标系是b系,就是我们飞行器的坐标系。对于四元数法的姿态解算,需要求取的就是四元数的值;方向余弦矩阵(用于表示n系和b系的相对关系)中的元素本来应该是三角函数,这里由于使用四元数法,所以矩阵中的元素就成了四元数。所以姿态解算的任务就是求解由四元数构成的方向余弦矩阵nCb(nCb表示从b系到n的转换矩阵,同理,bCn表示从n系到b的转换矩阵,它们的关系是转置)。
显然,上述矩阵是有误差存在的。对于一个确定的向量n,用不同的坐标系表示时,他们所表示的大小和方向一定是相同的。但是由于这两个坐标系的转换矩阵存在误差,那么当一个向量经过这么一个有误差存在的旋转矩阵变换后,在另一个坐标系中肯定和理论值是有偏差的,我们通过这个偏差来修正这个旋转矩阵。这个旋转矩阵的元素是四元数,这就是说修正的就是四元数,于是乎姿态就这样被修正了,这才是姿态解算的原理。姿态解算求的是四元数,是通过修正旋转矩阵中的四元数来达到姿态解算的目的,而不要以为通过加速度计和地磁计来修正姿态,加速度计和地磁计只是测量工具和载体,通过这两个器件表征旋转矩阵的误差存在,然后通过算法修正误差,修正四元数,修正姿态。
加速度计修正pitch_roll
加速度计可以修正pitch_roll,但是我们必须要考虑离心加速度(centrifugalacceleration),离心加速度就等于旋转率向量(即gyro vector)和速度向量的叉积(没有原因,平均得来的并且还相当准确,速度可以用GPS获取)。我们假设飞机方向和X轴平行。

在机体上测得的重力的为:

Pitch_roll的旋转修正向量是由DCM的Z行与归一化以后的重力参考向量的叉积。
在n系中,加速度计输出为,经过bCn(用四元数表示的转换矩阵)转换之后到b系中的值为;在b系中,加速度计的测量值为,现在和均表示在b系中的竖直向下的向量,由此,我们来做向量积(叉积),得到误差,利用这个误差来修正bCn矩阵,于是四元数就在这样一个过程中被修正了。但是,由于加速度计无法感知z轴上的旋转运动,所以还需要用地磁计来进一步补偿。
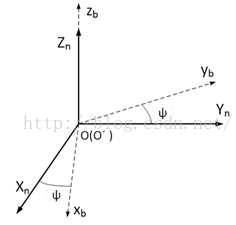
加速度计在静止时测量的是重力加速度,是有大小和方向的;同理,地磁计同样测量的是地球磁场的大小和方向,只不过这个方向不再是竖直向下,而是与x轴(或者y轴)呈一个角度,与z轴呈一个角度。记作,假设x轴对准北边,所以by=0,即。倘若知道bx和bz的精确值,那么就可以采用和加速度计一样的修正方法来修正。只不过在加速度计中,在n系中的参考向量是,变成了地磁计的。如果我们知道bx和bz的精确值,那么就可以摆脱掉加速度计的补偿,直接用地磁计和陀螺仪进行姿态解算,但是你看过谁只用陀螺仪和地磁计进行姿态解算吗?没有,因为没人会去测量当地的地磁场相对于东北天坐标的夹角,也就是bx和bz(插曲:关于这个bx和bz的理解:可以对比重力加速度的理解,就像vx vy vz似的,因为在每一处的归一化以后的重力加速度都是0 0 1然后旋转到机体坐标系,而地球每一处的地磁大小都不一样的,不能像重力加速度那样直接旋转得到了,只能用磁力计测量到的数据去强制拟合。)。那么现在怎么办?前面已经讲了,姿态解算就是求解旋转矩阵,这个矩阵的作用就是将b系和n正确的转化直到重合。现在我们假设nCb旋转矩阵是经过加速度计校正后的矩阵,当某个确定的向量(b系中)经过这个矩阵旋转之后(到n系),这两个坐标系在XOY平面上重合(参考DCM IMU:Theory的Drift cancellation部分),只是在z轴旋转上会存在一个偏航角的误差。下图表示的是经过nCb旋转之后的b系和n系的相对关系。可以明显发现加速度计可以把b系通过四元数法从任意角度拉到与n系水平的位置上,此时只剩下一个偏航角误差。这也是为什么加速度计无法修正偏航的原因。
为什么在word中使用公式编译器编辑的公式没办法复制到CSDN中呢????????????
此方式在数学上没有任何问题,但是由于地磁传感器极易受到各种干扰,而此算法又将地磁传感器所指示的方向过度的融入到了姿态当中,导致实际使用中数据会非常不稳定。怪不得crazypony的算法中没有使用磁力计修正YAW,这应该就是原因所在吧。
六、来一点ardupilot源码分析
就理解了一个通过gyro_vector更新DCM的算法,这个应该是在renormalization直接就需要了解,可以前期没理解到底是干嘛的,现在补上;关于renormalization的算法可以参考上一篇博文。
姿态解算过程中不仅需要修正陀螺仪的各种errors,还需要实时的更新的DCM。上周一直没能理解的一个问题,在AP_AHRS_DCM.cpp中的matrix_update(delta_t),就是实时更新DCM矩阵的,源码如下,这一部分研究了很久,需要的基础知识比较多。先上源码
- // update the DCM matrix using only the gyros
- Void AP_AHRS_DCM::matrix_update(float _G_Dt)
- {
- _omega.zero();
- // average across first two healthy gyros. This reduces noise on
- // systems with more than one gyro. We don't use the 3rd gyro
- // unless another is unhealthy as 3rd gyro on PH2 has a lot more
- // noise
- uint8_t healthy_count = 0;
- Vector3f delta_angle;
- for (uint8_t i=0; i<_ins.get_gyro_count(); i++) {
- if (_ins.get_gyro_health(i) && healthy_count < 2) {
- Vector3f dangle;
- if (_ins.get_delta_angle(i, dangle)) {
- healthy_count++;
- delta_angle += dangle;
- }
- }
- }
- if (healthy_count > 1) {
- delta_angle /= healthy_count;
- }
- if (_G_Dt > 0) {
- _omega = delta_angle / _G_Dt;
- _omega += _omega_I;
- _dcm_matrix.rotate((_omega + _omega_P + _omega_yaw_P) * _G_Dt);
- }
- }
首先就是通过陀螺仪获取两次gyro_vector,然后取平均以降低误差;然后就是比较专业的算法实现_dcm_matrix.rotate((_omega +_omega_P + _omega_yaw_P) * _G_Dt)了。进入到matrix3.cpp中有rotate()函数,该函数就是实现DCM更新的算法实现,算法主要是用陀螺仪的输出值与DCM矩阵的乘积再加回到DCM中去,处理过程中使用了离散化的概念,即dcm(k+1)=dcm(k)+增量,因为公式里有求导,必须离散化后才能计算机处理,感谢青龙的指导。
- // apply an additional rotation from a body frame gyro vector
- // to a rotation matrix.
- template <typename T>
- void Matrix3<T>::rotate(const Vector3<T> &g)
- {
- Matrix3<T> temp_matrix;
- temp_matrix.a.x = a.y * g.z - a.z * g.y;
- temp_matrix.a.y = a.z * g.x - a.x * g.z;
- temp_matrix.a.z = a.x * g.y - a.y * g.x;
- temp_matrix.b.x = b.y * g.z - b.z * g.y;
- temp_matrix.b.y = b.z * g.x - b.x * g.z;
- temp_matrix.b.z = b.x * g.y - b.y * g.x;
- temp_matrix.c.x = c.y * g.z - c.z * g.y;
- temp_matrix.c.y = c.z * g.x - c.x * g.z;
- temp_matrix.c.z = c.x * g.y - c.y * g.x;
- (*this) += temp_matrix;//增加累加到原始数据上
- }


最近事情好多啊,愁死了,谁能帮我分担一点啊~~~~
昨天去三星见了一位智能家居group的总监,聊了以后才发现自己有多low啊,我的BLE怎么搞,大公司都在做垄断化、平台化,看来毕业只能硬着头皮进大公司了,希望能找个好工作,谁在外企啊,帮我介绍工作啊,啊啊, 啊, ,啊, 啊。。。。
写的语无伦次的,凑合看吧








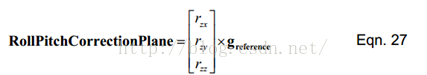
















 574
574

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








