python 时间序列ARIMA模型预测

时间序列ARIMA模型
平稳性检验与纯随机性检验
python时序预测的7种方法

ARIMA模型

安装statsmodels

pip install statsmodels

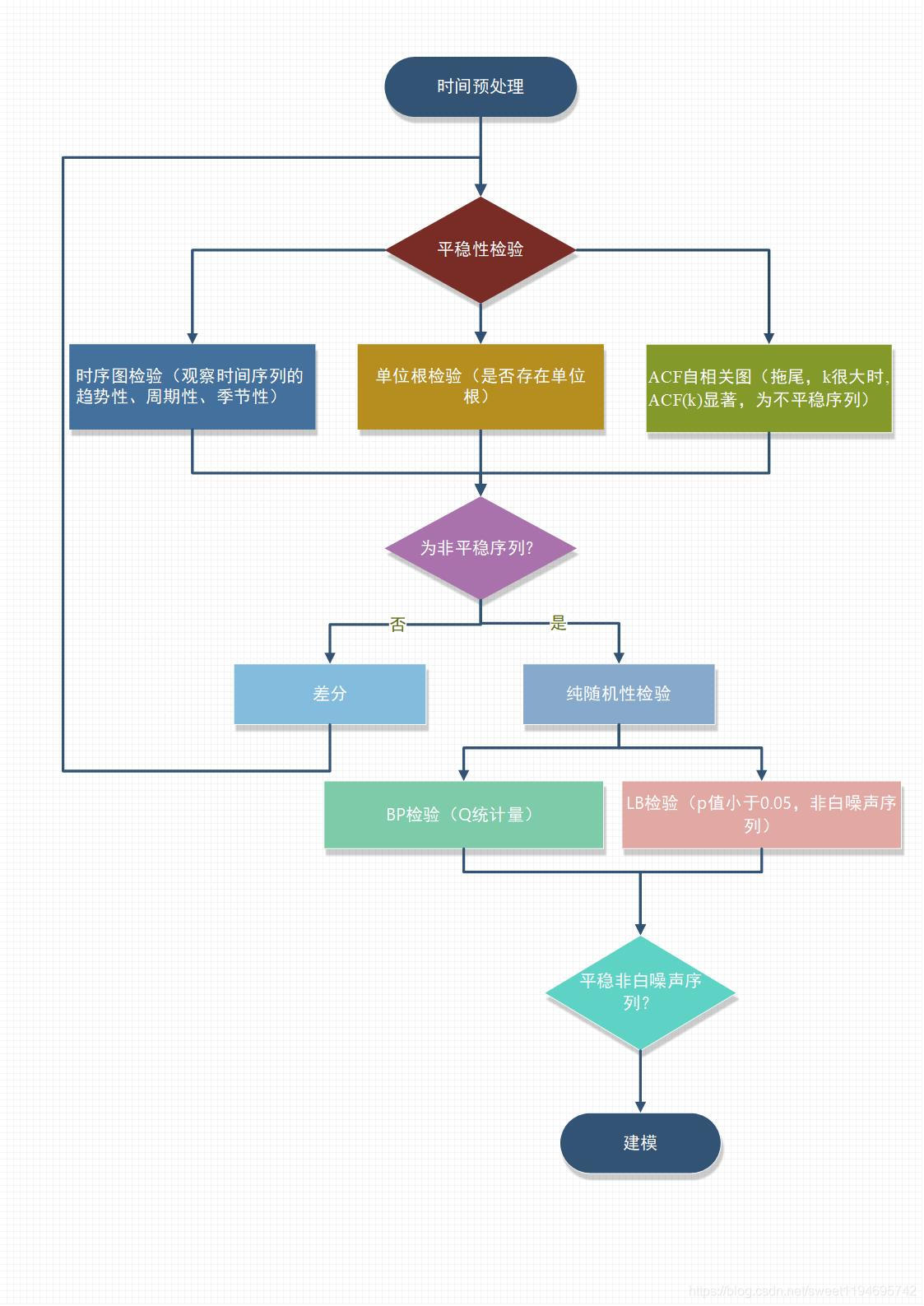
建模过程

一、时间序列预处理

注意：

1、白噪声时序也是平稳序列，但是没有分析的价值，无信息可提取。
2、平稳序列不一定是白噪声序列；
3、无论是时序图还是 ACF 图，使用它们作为检验方法时都具有较强的主观性，没有引入客观的统计量。
   因此，时序图与 ACF 图仅能用来排除非平稳时序，不能用来判断一个时序是否是平稳时序！
   即描述性检验方法仅仅是为计量性检验方法作一个初步筛选，如果时序没有通过描述性检验方法，就不需要进行计量性检验了；
   而即使时序通过了描述性检验方法，仍需要进行计量性检验来进一步确认时序为平稳时序。
4、平稳性检验可以通过时序图、ACF 图等描述性方法，但依然要使用 ADF 检验、PP 检验来最终判断。
5、平稳的非白噪声序列：均值和方差是常数，最常用ARMA拟合模型；
6、非平稳序列均值方差不稳定，一般将其转为平稳序列，可用ARMA；如果一个序列差分后具有平稳性，则该序列为差分平稳序列，可用ARIMA。

误区：

1、仅仅通过时序图与 ACF 图就断定一个时序是平稳时序：时序图与 ACF 图仅仅只能用于判断非平稳时序，不能用于判断平稳时序。
2、不画时序图与 ACF 图，直接对时序进行 ADF 检验与 PP 检验：描述统计是必不可少的步骤，通过时序图与 ACF 图可以清楚看出时序的趋势性与周期性。
3、在正式建模之前不检验时序的纯随机性，认为仅仅检验时序的平稳性就足够了：白噪声时序也是平稳序列，但是没有分析的价值。
4、在正式建模之后不检验残差序列的纯随机性：残差序列的纯随机性检验有点类似于多元回归中的 F 检验，检验的是模型总体的显著性水平。

1)平稳性检验

a)时序图检验

观察时间序列的趋势性、周期性、季节性

data.RUL.plot()

b) acf 自相关系数和 pacf 偏相关系数

from statsmodels.tsa.stattools import acf, pacf
##通过观察PACF和ACF截尾，分别判断p、q的值。
lag_acf = acf(y, nlags=80)  #自相关
lag_pacf = pacf(y, nlags=80, method='ols') #偏自相关
fig, axes = plt.subplots(1,2, figsize=(25,8))
pd.Series(lag_acf).plot(kind = 'bar', ax=axes[0])
pd.Series(lag_pacf).plot(kind = 'bar', ax=axes[1])

或者