9.6 多元函数微分学的几何应用

 

第六节 多元函数微分学的几何应用

一、一元向量值函数及其导数

1. 向量值函数的定义和基本性质

一元向量值函数是一元函数的一个扩展，其中自变量取实数值，但因变量取值为向量。考虑空间曲线的参数方程可以表达为向量方程：

这里 𝑟r 是从坐标系原点到点 𝑀M 的向量，随时间 𝑡t 改变而改变，描述了空间中的一条曲线，称为曲线 ΓΓ 的向量方程。

定义

• 定义1: 设数集 𝐷⊂𝑅D⊂R，映射 𝑓:𝐷→𝑅𝑛f:D→Rn 称为一元向量值函数，记为 𝑟=𝑓(𝑡)r=f(t)，其中 𝑡t 是自变量，𝑟r 是因变量。

2. 向量值函数的极限和连续性

向量值函数的极限和连续性定义与常规的数量函数类似，但是它们应用于向量的每个分量。

• 定义2: 如果存在常向量 𝑟0r0​ 使得对于任意正数 𝜖ϵ，总存在 𝛿>0δ>0 使得当 0<∣𝑡−𝑡0∣<𝛿0<∣t−t0​∣<δ 时，有 ∣𝑓(𝑡)−𝑟0∣<𝜖∣f(t)−r0​∣<ϵ，则称向量 𝑟0r0​ 是向量值函数 𝑓(𝑡)f(t) 当 𝑡→𝑡0t→t0​ 时的极限，记为 lim⁡𝑡→𝑡0𝑓(𝑡)=𝑟0limt→t0​​f(t)=r0​。

3. 导数和微分的定义

向量值函数的导数定义为向量值函数在某点的瞬时变化率。

• 定义3: 设向量值函数 𝑟=𝑓(𝑡)r=f(t) 在点 𝑡0t0​ 的某一邻域内有定义，如果极限

  

  存在，则称这个极限向量为向量值函数 𝑓(𝑡)f(t) 在 𝑡0t0​ 处的导数或导向量。

4. 向量值函数的几何意义和应用

切向量的几何意义

对于空间曲线 ΓΓ，其由向量值函数 𝑟=𝑓(𝑡)r=f(t) 描述，向量值函数的导数 𝑓′(𝑡)f′(t) 在几何上表示曲线在对应点的切向量，其方向与曲线在该点的切线方向一致。

应用示例

1. 速度与加速度向量：如果 𝑟=𝑓(𝑡)r=f(t) 表示物体在空间中的位置向量，则 𝑓′(𝑡)f′(t) 表示物体在时刻 𝑡t 的速度向量，𝑓′′(𝑡)f′′(t) 表示加速度向量。

2. 特定曲线的单位切向量计算：

   • 给定曲线 𝑟=𝑓(𝑡)=(𝑡2+1,4𝑡−3,2𝑡2−6𝑡)r=f(t)=(t2+1,4t−3,2t2−6t)，在 𝑡=2t=2 时的切向量 𝑓′(2)=(4,4,2)f′(2)=(4,4,2)。
   • 计算单位切向量：

3. 滑翔机的动力学分析：

   • 滑翔机的路径由 𝑟=𝑓(𝑡)=(3cos⁡𝑡,3sin⁡𝑡,𝑡2)r=f(t)=(3cost,3sint,t2) 给出。
   • 在任意时刻 𝑡t 的速度 𝑣(𝑡)=(−3sin⁡𝑡,3cos⁡𝑡,2𝑡)v(t)=(−3sint,3cost,2t) 和加速度 𝑎(𝑡)=
   • 速度与加速度正交的时刻 𝑡=0t=0。

这些概念不仅理论丰富，而且在解决实际物理问题和工程问题中具有广泛的应用。

 

 

 

第六节 多元函数微分学的几何应用

二、空间曲线的切线与法平面

设空间曲线的参数方程为 𝑟(𝑡)=(𝑥(𝑡),𝑦(𝑡),𝑧(𝑡))r(t)=(x(t),y(t),z(t))，其中 𝑡t 在区间 [𝑎,𝛽][a,β] 上，并假定 𝑥(𝑡),𝑦(𝑡),𝑧(𝑡)x(t),y(t),z(t) 在该区间上均可导，且它们的导数不同时为零。我们将探讨如何求得曲线在其上某点 𝑀(𝑥0,𝑦0,𝑧0)M(x0​,y0​,z0​) 的切线和法平面方程。

切线方程的推导

设与点 𝑀M 对应的参数为 𝑡0t0​，向量值函数 𝑓(𝑡)=(𝜙(𝑡),𝜓(𝑡),𝜔(𝑡))f(t)=(ϕ(t),ψ(t),ω(t))，在 𝑡0t0​ 的导向量 𝑇=𝑓′(𝑡0)=(𝜙′(𝑡0),𝜓′(𝑡0),𝜔′(𝑡0))T=f′(t0​)=(ϕ′(t0​),ψ′(t0​),ω′(t0​)) 表示曲线在 𝑀M 处的切向量。因此，曲线在点 𝑀M 处的切线方程可以表达为：

法平面方程的推导

通过点 𝑀M 且与切线垂直的平面称为曲线在点 𝑀M 处的法平面。它是通过点 𝑀(𝑥0,𝑦0,𝑧0)M(x0​,y0​,z0​) 且以 𝑇=𝑓′(𝑡0)T=f′(t0​) 为法向量的平面，因此法平面方程为：

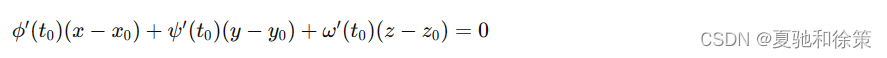
示例：求切线及法平面方程

例4: 求曲线 𝑥=𝑡,𝑦=𝑡2,𝑧=𝑡3x=t,y=t2,z=t3 在点 (1,1,1)(1,1,1) 处的切线及法平面方程。

解： 由于 𝑥′=1,𝑦′=2𝑡,𝑧′=3𝑡2x′=1,y′=2t,z′=3t2，且给定的点 (1,1,1)(1,1,1) 对应的参数 𝑡0=1t0​=1，所以 𝑇=(1,2,3)T=(1,2,3)。

切线方程为：

𝑥−1=2(𝑦−1)=3(𝑧−1)x−1=2(y−1)=3(z−1)

法平面方程为：

(𝑥−1)+2(𝑦−1)+3(𝑧−1)=0(x−1)+2(y−1)+3(z−1)=0

即：

𝑥+2𝑦+3𝑧=6x+2y+3z=6

此示例清楚地展示了如何利用向量值函数的导数来找到空间曲线的切线和法平面，这在多元微分学中的几何应用是基础且核心的部分。

 

 

 

第六节 多元函数微分学的几何应用

三、曲面的切平面与法线

曲面的隐式表示

考虑由隐式方程 𝐹(𝑥,𝑦,𝑧)=0F(x,y,z)=0 给出的曲面。设 𝑀(𝑥0,𝑦0,𝑧0)M(x0​,y0​,z0​) 是曲面上的一点，并且函数 𝐹F 的偏导数在该点连续且不全为零。在曲面上任意引出一条通过点 𝑀M 的曲线，其参数方程为 𝑥=𝜙(𝑡)x=ϕ(t), 𝑦=𝜓(𝑡)y=ψ(t), 𝑧=𝜔(𝑡)z=ω(t)，其中 𝑡=𝑡0t=t0​ 对应于点 𝑀M。

切线与切平面

对于曲线 ΓΓ 在曲面上的表达 𝐹(𝜙(𝑡),𝜓(𝑡),𝜔(𝑡))=0F(ϕ(t),ψ(t),ω(t))=0，由复合函数的全导数为零，得：

这显示出曲线 ΓΓ 在点 𝑀M 处的切向量 𝑇=(𝜙′(𝑡0),𝜓′(𝑡0),𝜔′(𝑡0))T=(ϕ′(t0​),ψ′(t0​),ω′(t0​)) 与向量 𝑛=(𝐹𝑥(𝑥0,𝑦0,𝑧0),𝐹𝑦(𝑥0,𝑦0,𝑧0),𝐹𝑧(𝑥0,𝑦0,𝑧0))n=(Fx​(x0​,y0​,z0​),Fy​(x0​,y0​,z0​),Fz​(x0​,y0​,z0​)) 垂直。因此，所有通过点 𝑀M 的曲线的切线都在同一个平面上，即曲面的切平面，其方程为：

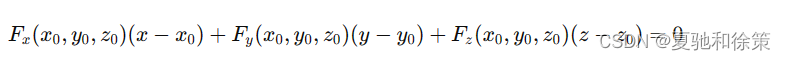
法线方程

曲面在点 𝑀M 处的法线方程可以由切平面的法向量 𝑛n 直接给出：

显式表示的曲面

对于显式方程 𝑧=𝑓(𝑥,𝑦)z=f(x,y)，我们可以设置 𝐹(𝑥,𝑦,𝑧)=𝑓(𝑥,𝑦)−𝑧F(x,y,z)=f(x,y)−z，于是有：

此时，法向量为 (𝑓𝑥(𝑥0,𝑦0),𝑓𝑦(𝑥0,𝑦0),−1)(fx​(x0​,y0​),fy​(x0​,y0​),−1)，切平面方程简化为：

或等价地：

例子：球面与旋转抛物面的切平面与法线

例6：球面 𝑥2+𝑦2+𝑧2=14x2+y2+z2=14 在点 (1,2,3)(1,2,3)

• 法向量：𝑛=(2𝑥,2𝑦,2𝑧)n=(2x,2y,2z)，在点 (1,2,3)(1,2,3) 处为 (2,4,6)(2,4,6)。
• 切平面方程：2(𝑥−1)+4(𝑦−2)+6(𝑧−3)=02(x−1)+4(y−2)+6(z−3)=0，简化为 𝑥+2𝑦+3𝑧−14=0x+2y+3z−14=0。
• 法线方程：𝑥−1=2(𝑦−2)=3(𝑧−3)x−1=2(y−2)=3(z−3)。

例7：旋转抛物面 𝑧=𝑥2+𝑦2−1z=x2+y2−1 在点 (2,1,4)(2,1,4)

• 法向量：𝑛=(4,2,−1)n=(4,2,−1)。
• 切平面方程：4(𝑥−2)+2(𝑦−1)−(𝑧−4)=04(x−2)+2(y−1)−(z−4)=0，简化为 4𝑥+2𝑦−𝑧−6=04x+2y−z−6=0。
• 法线方程：4𝑥=2𝑦=−𝑧4x=2y=−z。

这些例子展示了如何应用微分学的原理来解决曲面的切平面和法线问题，这在多元微分学和空间几何中是非常基础和重要的概念。