1.什么是非线性最小二乘问题
所谓“非线性最小二乘优化问题”就是指:目标函数是非线性函数平方和,具体形式为:
可以看到,目标函数为n个函数平方和
2.如何求解非线性最小二乘问题
LM算法是求解非线性最小二乘问题的一个很稳定的方法,实际应用中经常使用,之前都是自己编写程序,今天偶然发现matlab居然自带了LM优化算法
3.Matlab中的LM算法函数
matlab提供了一个求解非线性最小二乘问题的优化函数lsqnonlin
Matlab提供了2种计算方式,分别为with Jacobian和without Jacobian两种方式
以如下优化函数为例:min
3.1 without Jacobian
step1:myfun.m函数
myfun函数作用是计算目标函数
% 函数输入是向量x,返回值是目标函数值
function F = myfun(x)
k = 1:10;
F = 2 + 2*k-exp(k*x(1))-exp(k*x(2));step2: 利用lsqnonlin函数求解优化问题
x0 = [0.3,0.4]; % Starting guess
[x,resnorm,res,eflag,output1] = lsqnonlin(@myfun,x0); % Invoke optimizer注意到,在mufun函数中,并没有计算Jacobian
经过72步迭代后,可以得到最优解x和残差resnorm
x = 0.2578 0.2578;resnorm = 124.3622
3.2 with Jacobian
step1:myfun.m函数
myfun函数作用是计算目标函数及目标函数的Jacobian
% 函数输入是向量x,返回值是目标函数值F和Jacobian
function [F,J] = myfun(x)
k = 1:10;
F = 2 + 2*k-exp(k*x(1))-exp(k*x(2));
if nargout > 1 %如果返回值为2个
J = zeros(10,2);
J(k,1) = -k.*exp(k*x(1));
J(k,2) = -k.*exp(k*x(2));
endstep2:设置solver
opts = optimoptions(@lsqnonlin,’SpecifyObjectiveGradient’,true);
step3: 利用lsqnonlin函数求解优化问题
x0 = [0.3 0.4]; % Starting guess
[x,resnorm,res,eflag,output2] = lsqnonlin(@myfun,x0,[],[],opts);经过24步迭代后,可以得到最优解x和残差resnorm
x = 0.2578 0.2578;resnorm = 124.3622
可以看到:
The advantage to using a Jacobian is that the solver takes fewer function evaluations, 24 instead of 72.





 本文介绍了非线性最小二乘问题及其解决方法——LM算法,并通过Matlab自带的lsqnonlin函数进行了实例演示,对比了使用与不使用Jacobian的方式。
本文介绍了非线性最小二乘问题及其解决方法——LM算法,并通过Matlab自带的lsqnonlin函数进行了实例演示,对比了使用与不使用Jacobian的方式。
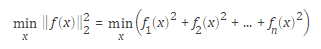
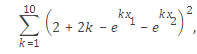
















 503
503

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








