漫步数学分析二——欧几里得空间

$\textbf{定义3}$ 欧几里得$n-$空间是由所有有序的$n$ 元实数组成的并且用$R^n$来表示。象征性的符号为

$$R^n=\{(x_1,\ldots,x_n)|x_1,\ldots,x_n\in R\}$$

因此$R^n$是$R$与自身进行$n$次笛卡尔乘积的结果，可以写成$R^n=R\times\cdots\times R$。

$R^n$的元素通常用单个字母来表示，即$x=(x_1,\ldots,x_n)$，并且称$x$是$R^n$中的一个点。

加法和标量乘法用通常的方式进行定义：

$$(x_1,\ldots,x_n)+(y_1,\ldots,y_n)=(x_1+y_1,\ldots,x_n+y_n)$$

乘法为

$$\alpha(x_1,\ldots,x_n)=(\alpha x_1,\ldots,\alpha x_n)\quad\text{for}\ \alpha\in R$$

这些运算的几何意义如图$\ref{fig:1-3}$所示，该图是三空间的情况即$n=3$。

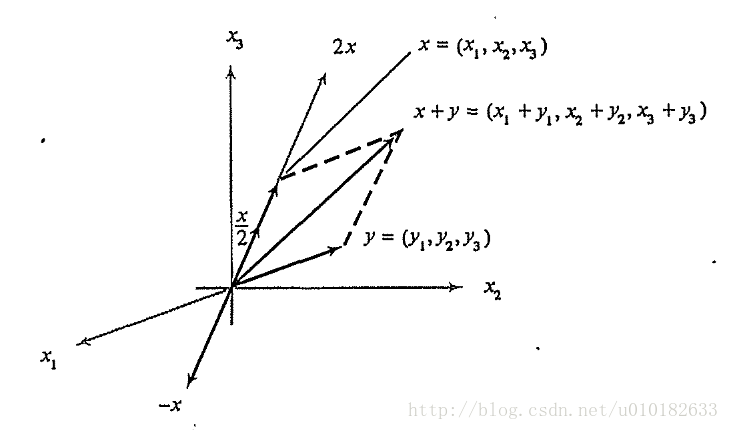
图1：加法和标量乘法

$\textbf{定理4}$ 满足加法与标量乘法的欧几里得$n-$空间是一个$n$为向量空间。

证明的方法就是直接检查是否满足向量空间的公理，这里不再讨论。这个定理在我们的意料之中，毕竟向量空间是欧几里得空间中向量基本性质的抽象，接下来我们就能通过展示$R^n$ 有$n$个向量的基来说明它的维数是$n$，例如，标准基$\{e_1=(1,0,\ldots,0),e_2=(0,1,0,\ldots,0),\ldots,e_n=(0,0,\ldots,0,1)\}$。

在标准基中，$x=(x_1,\ldots,x_n)$的元素就是$x_1,\ldots,x_n$，而对于$R^n$的其他基，这些元素将是不同的，这就意味着如果用$e_1,\ldots,e_n$来表示标准基，那么$x=\Sigma_{i=1}^n x_ie_i$，但是如果$f_1,\ldots,f_n$ 是另一组基，那么$x=\Sigma_{i=1}^ny_if_i$中的$y_1,\ldots,y_n$是不同的值。

下面是$R^n$中的一些基本运算。

$\textbf{定义4}$ $R^n$中向量$x$的长度(length)或范数(norm)定义为

$$\Vert x\Vert=\left(\sum_{i=1}^nx_i^2\right)^{1/2}$$

其中$x=(x_1,\ldots,x_n)$，两个向量$x,y$之间的距离(distance) 是一个实数并定义如下

$$d(x,y)=\Vert x-y\Vert=\left\{\sum_{i=1}^n(x_i-y_i)^2\right\}^{1/2}$$

$x,y$的内积(inner product)定义为

$$\langle x,y\rangle=\sum_{i=1}^n x_iy_i$$

因此我们有$\Vert x\Vert^2=\langle x,x\rangle$。对于$R^3$空间，读者对$\langle x,y\rangle$ 比较熟悉，即$\langle x,y\rangle=\Vert x\Vert\Vert y\Vert\cos\theta$，其中$\theta$是$x,y$夹角的余弦值，如图$\ref{fig:1-4}$所示。

现在我们总结一下这些运算的基本性质：

$\textbf{定理5}$ 对于$R^n$中的向量，我们有
$\textrm(I)$内积的性质

1. $\langle x,y_1+y_2\rangle=\langle x,y_1\rangle+\langle x,y_2\rangle$
2. 对于每个实数$\alpha,\langle x,\alpha y\rangle=\alpha\langle x,y\rangle$
3. $\langle x,y\rangle=\langle y,x\rangle$
4. $\langle x,x\rangle\geq0$，当且仅当$x=0$时$\langle x,x\rangle=0$
5. $|\langle x,y\rangle\leq\Vert x\Vert\Vert y\Vert|$(柯西施瓦兹不等式(Cauchy-Schwarz inequality))。
   注意：$\textrm{(v)}$可从$\textrm{(i)-(iv)}$推出。

$\textrm(II)$范数的性质

1. $\Vert x\Vert\geq0$
2. $\Vert x\Vert=0$当且仅当$x=0$
3. 对于每个实数$\alpha,\Vert\alpha x\Vert=|\alpha|\Vert x\Vert$
4. $\Vert x+y\Vert\leq\Vert x\Vert+\Vert y\Vert$(三角不等式(triangle inequality))

$\textrm(III)$距离的性质
1.$d(x,y)=d(y,x)$
2.$d(x,y)\geq0$
3.$d(x,y)=0$当且仅当$x=y$
4.$d(x,y)\leq d(x,z)+d(z,y)$(也称为三角不等式)

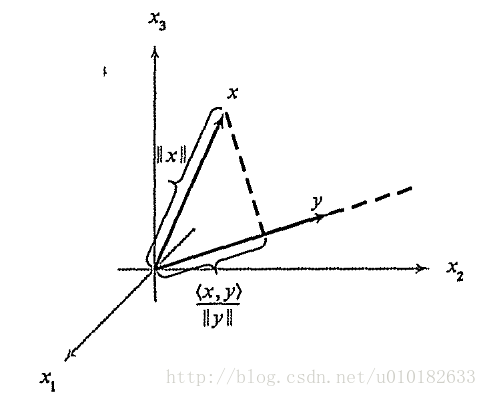
图2：长度和内积

这些性质都要非常明显的几何意义，例如 $\textrm{(II)(III)}$中的 $\textrm{(iv)}$表达的就是三角形的一边长小于或等于其他两边长的和(图 $\ref{fig:1-5}$)。

对于一个集合，如果其中的函数$d$满足规则$\textrm{(III)}$，那么称该集合为度量空间；对于一个向量空间，如果其中的范数满足规则$\textrm{(II)}$，那么称该空间为范数空间；对于一个向量空间，如果其中的内积满足规则$\textrm{(I)}$，那么称该空间为内积空间。

我们回忆一下线性代数中线性子空间的符号，特别地，$R^n$ 中$(n-1)$维线性子空间称为超平面。仿射超平面就是集合$x+H$，其中$H$是一个超平面且$x\in R^n$；$x+H$意味着所以$x+y$组成的集合，其中$y$取$H$上的值；因此$x+H=\{x+y|y\in H\}$，如图$\ref{fig:1-6}$所示。

最后我们推广一下$R^3$中的概念，我们称$x,y\in R^n$是正交的(orthogonal)当且仅当$\langle x,y\rangle=0$。两个子空间$S,T$是正交的，当且仅当对于所以的$x\in S,y\in T,\langle x,y\rangle=0$。进一步来讲，如果$S,T$生成$R^n$，那么称他们是正交补(orthogonal complements)，当且仅当$S,T$是正交的且他们的维数和为$n$时他们才会是正交补。我们定义$S^{\perp}=\{y\in R^n|\langle x,y\rangle=0\ \text{for all}\ x\in S\}$，那么不难看出$S,S^{\perp}$是正交补。除了一些线性代数的基本概念外，我们不需要太多线性代数知识，所以我们不在进行进一步的讨论。

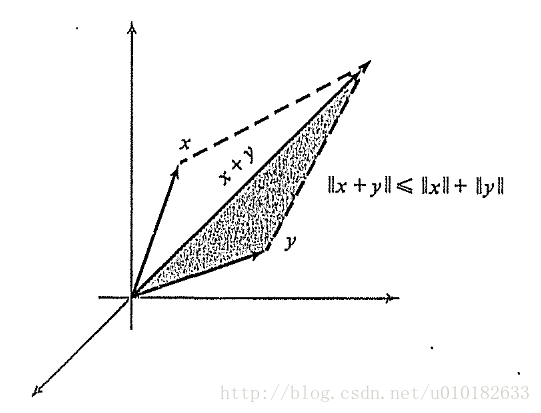
图3：三角不等式

$\textbf{例1：}$求出连接点(1,1,1)到(3,2,0)线段的长度。

$\textbf{解：}$这个长度就是向量$(3,2,0)-(1,1,1)=(2,1,-1)$的长度，其长度为

$$\Vert(2,1,-1)\Vert=\sqrt{2^2+1^2+(-1)^2}=\sqrt6$$

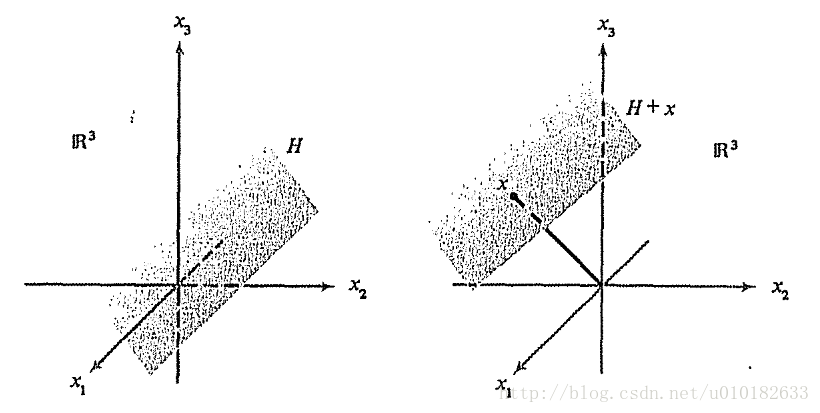
图4：超平面和仿射超平面



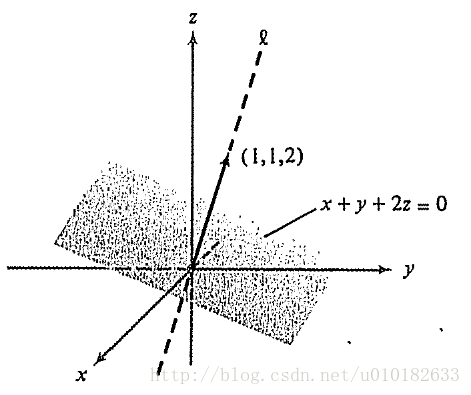
图5：正交补

$\textbf{例2：}$在 $R^3$中，找出直线 $x=y=z/2$的正交补(或者其他符号表示为 $x_1=x_2=x_3/2$)。

$\textbf{解：}$我们称这条直线为$l$，它是由向量(1,1,2) 生成的一维子空间(图$\ref{fig:1-7}$)，正交补是一个平面(因为是一个子空间所以过原点)，所以有如下的形式

$$Ax+By+Cz=0$$

即

$$\langle(A,B,C),(x,y,z)\rangle=0$$

其中(A,B,C)是平面的法向量；但是(1,1,2)是与该平面垂直所以正交补是平面

$$x+y+2z=0$$