惯性导航一(基础篇：科里奥利力和哥氏定理)

本节作为惯性导航基础篇，通过推导科里奥利力、哥/科氏加速度以及哥/科氏定理，加深理解，主要涉及了物理学相关知识。后续会推导比力方程，捷联系统速度、位置算法相关内容。

一、扩展知识

1.1 矢量加减

在做矢量加减时，各个矢量必须是由同一坐标系下测得的才成立，因为不同坐标系下对同一矢量的测量可能是不一样的（参见哥氏定理）

1.2 牛顿绝对时空观

牛顿绝对时空观包括空间的绝对性和时间间隔的绝对性，而与参考系的运动状态无关。适用条件是两参考系的相对运动速度小于光速，当接近光速时，绝对时空观失效。

1.2.1 空间的绝对性

空间两点的距离不管从那个坐标系测量，结果都相同。也就是说空间的位置矢量，在不同坐标系下测得的其矢量的大小和方向是一样的。

1.2.2 时间间隔的绝对性

不同坐标系下观察到的两事件之间的时间间隔相同。

1.3 为什么要引入非惯性系、惯性力

我们知道牛顿第一和第二定律只在惯性系下成立，而自然界中存在的绝大多数都是非惯性系，为了在非惯性系下方便的进行运算(使牛二定律在非惯性系下形式上成立)，所以引入了惯性力。
在惯性系中，根据牛一和牛二定律，满足 （这里下表a表示相对惯性系的绝对加速度），而在非惯性系中，由于牵连运动的存在（平动或者转动）， （绝对加速度≠相对加速度），即在 非惯性系下 ，也就是牛一和牛二定律在非惯性系下不成立。为了在非惯性系合力于相对加速度形式上满足
，在非惯性系创建出了很多虚拟力（称为惯性力），这些力本身是不存在的（其特点是找不出施加该力的作用源，没有反作用力，惯性系下不存在该力）。常见的惯性力有圆周运动的离心力，相对匀速转动的参考系有相对运动的科里奥利力。

1.4 为什么要引入绝对运动、相对运动和牵连运动

相对于某一参考系（体）的复杂运动可以分解成相对于其他参考系（体）的几个简单运动，不同的坐标系之间会涉及静参考系、动参考系，参考系之间就会涉及绝对运动、牵连运动和相对运动的概念。

1.5 部分概念定义

静系：惯性坐标系称为静系；
动系：相对惯性坐标系运动的坐标系称为动系；
绝对运动：动点相对于静系的运动；
相对运动：动点相对于动系的运动；
牵连运动：动系相对于静系的运动；
绝对轨迹：动点在静系上的轨迹称为绝对轨迹；
绝对速度：动点相对于静系上的速度称为绝对速度；
绝对加速度：动点相对于静系的加速度称为绝对加速度；
相对轨迹：动点在动系上的轨迹称为相对轨迹；
相对速度：动点相对于动系上的速度称为相对速度；
相对加速度：动点相对于动系的加速度称为相对加速度；
牵连点：指定瞬时在动系上与动点重合的那一点成为牵连点；
牵连速度：牵连点的速度称为牵连速度；
牵连加速度：牵连点的加速度称为牵连加速度；
注1：由于牵连运动是动系相对于静系的运动（刚体），而不是一个点的相对运动。有的定义直接把牵连速度/加速度定义为动系相对于静系的速度/加速度，这么定义没错，但是并不能用来引入进行计算，毕竟刚体选取指定点针对该点进行分析才有意义，因此引入了牵连点的概念。
注2：牵连点是只某个瞬间与动点重合位于动系上的点，为什么强调瞬时性，是因为求牵连速度表示时该瞬间的牵连点相对于动系的速度（动系动而牵连点是瞬时固定的）。
注3：实际运算中往往牵连运动比较难计算

1.6 绝对运动、相对运动、牵连运动速度的一种分析方法分析速度/加速度包括大小和方向，有些运动其静坐标系和动坐标系选取和运动状态识别比较复杂，在分析绝对、相对、牵连运动分开进行分析。

绝对运动分析：只保留静系和动点，分析动点相对于静系的运动。
相对运动分析：只保留动系和动点，分析动系处于不动状态下，动点自身的运动趋势。
牵连运动分析：只保留动系和牵连点，由于牵连点瞬时性(保持不变)，分析动系运动，由动系引起的牵连点的运动状态得到其牵连速度。（这种方法计算牵连速度更简单，动系有转动牵连线速度=旋转角速度×动系到牵连点矢径；动系平动牵连点的速度也就等于动系平动的速度）
注4：上面牵连点的瞬时性体现在由动系运动引起的牵连点的运动速度。
注5：上述只是一种解题方法，并不是说牵连运动是这么定义的。我们看牵连运动的定义是动系相对静系的运动，牵连速度是说牵连点的速度，方法与定义不要混淆。

二、点的速度合成定理

2.1 速度合成定律定义

点的速度合成定理：动点在某瞬时的绝对速度等于它在该时的瞬时牵连速度与相对速度的矢量和。即即绝对速度 = 牵连速度+相对速度()
注6：这里叫点的速度合成定理，但是实际上牵连运动是坐标系（刚体）的运动状态。
另：这里的牵连速度包括动系可能存在的平动牵连速度和转动牵连速度。

2.2 速度合成定理的推导

假设有静系和动系，设有一个动点P，其相对于静系原点的位置矢量为，相对于动系原点的位置矢量为，动系原点相对于相对静系原点的位置为 。一些资料上来得到则有下列位置变换的结论：，说绝对位置矢量 = 相对位置矢量 + 牵连位置矢量。其实严格来说不能直接得出该式子，在1.1说了，我们矢量的加减，各个矢量必须是相对同一个坐标系测得的，即这个式子准确的写法是，和都是相对静系测得的，而是相对动系测得的，这个式子成立的条件是相对于静系是相等的才成立，根据空间的绝对性，位置矢量在不同坐标系下测量值是一样的，即=。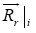

注7：这里的静系和动系不一定要是惯性系和非惯性系，有相对运动的两个参考系即可。

2.2.1 假设动系相对于静系只有平动：

按照牵连运动的分析方法，牵连点 (与动点P重合的点)的速度由动系平动引起，牵连点 的速度(牵连速度)即动系平动的运动速度。
设动系平动的速度为，那么此时牵连速度 ，在动系没有转动条件下，根据哥氏定理，有 即动系相对静系只有平动时，物体绝对速度 = 平动牵连速度 +相对速度。

2.2.2 动系除了平动外，还有恒定的转动角速度

动系在平动基础上，还有恒定的转动角速度，按照牵连运动的分析方法，牵连点(与动点P重合的点)的速度不仅包含动系平动引起的牵连速度 ，还包括由于动系转动引起的牵连线速度，。其 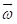为动系转动的角速度，半径为牵连点到动系原点的矢径 。
即动系在既有平动，又有转动的条件下，物体的绝对速度 = 平动牵连运动+(转动)牵连线速度+相对速度。

2.2.3 动系无平动，只有恒定的转动角速度

如果动系无平动，只有恒定的转动角速度，那么物体的绝对速度 = (转动)牵连线速度+相对速度，此时和 相同，没有 。即, 为原点到动点（牵连点的矢径），用微分形式表示即： 。
实际上，

有个更为通用的表达式：。用于
描述一个矢量在两个做相对旋转的坐标系m和n绝对变化率与相对变化率的关系，设矢量为，和 分别式在m和n坐标系内观察到的的时间变化率，为坐标系n相对m系的旋转角速度，这就是哥氏定理。

注8：哥氏定理中，矢量 并没有限制是什么矢量，即可能是位置矢量（求导后即绝对速度和相对速度的关系），也可能是速度矢量（求导后即绝对加速度和相对加速度的关系）、角速度矢量、加速度矢量。
注9：哥氏定理中的矢量指的是在m和n系中同一个矢量，不要混淆如果n系存在平动下计算速度过程中和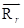，两者本身之间存在，并不是同一个矢量，我们利用哥氏定理可以说相对速度相对m系空间关系 = +相对n系的空间关系，但不能拿哥氏定理得到 相对m系的空间关系 =+ 相对n系的空间关系 。哥氏定理本身并不限制m和n系之间是否存在平动，但我们要确保的是使用的同一矢量。
注10：如果 =0，即m和n系之间没有相对转动，那么矢量相对于m系的变化率 和矢量相对于n系的变化率是相同的，即单纯的平动不影响该矢量其在m和n系下的时间变化率这个结论不仅适用于位置矢量，也适用于速度或加速度。

三、加速度关系

我们平时讨论的加速度都是相对惯性系的，当然也有相对非惯性系的。

3.1 假设动系相对静系只有平动：

假设动系相对于静系只有平动，相对静系的牵连加速度为
，动点相对于静系的加速度为 ，动点相对于动系的加速度为 。由点的速度合成定理，此时的牵连速度只有平动牵连速度，同时针对静系a下时间求导：
，得到，由哥氏定理知，两个坐标系没有相对转动满足静系a下观察到的 对时间的变化率和动系r下看到的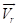对时间的变化率是相等的，有，得。即动系只有平动条件下：绝对加速度 = 平动牵连加速度+相对加速度， 。

3.2 在平动基础上，动系相对静系有恒定转动角速度：

如果在上述基础上，动系相对静系有恒定的转动角速度，则，同时相对静系a进行求导，有
即
由哥氏定理：
由哥氏定理：
有：

。
其中，为动点（牵连点）到动系的矢径，
为维持动点（牵连点）绕动系转动的牵连转动向心加速度，为哥/科氏加速度(又称为科里奥利力加速度)。

即当动系有相对于静系的加速平动和匀速转动时：
绝对加速度 = 平动牵连加速度+牵连转动向心加速度+哥氏加速度+相对加速度，。

3.3 如果动系相对静系没有加速平动(静止或匀速平动)

绝对加速度 =牵连转动向心加速度+哥氏加速度+相对加速度。
。
其中，为动点（牵连点）到动系的矢径，
为维持动点（牵连点）绕动系转动的牵连转动向心加速度，为哥/科氏加速度(又称为科里奥利力加速度)。

四、科里奥利力

通过上面的计算，我们知道在匀速转动的参考系下（非惯性系），有相对该参考系的运动物体会有哥氏加速度，这个加速度是真实存在的，大小为 。而科里奥利力是这么定义的，由哥氏加速度乘以质量m，并取相反方向，即 。由上面的计算我们知道，在动系r相对于静系a有平动和匀速的转动时，运动物体满足牛顿第二定律：
，指的是真实存在的力的合力。
在非惯性系下，形式上满足
，其中， 叫做牵连力，叫离心力（对应向心加速度，与其方向相反），叫科里奥利力，这些力都属于惯性力，是虚拟的力。