双边滤波原理理解

bilateral filter

双边滤波是一种保边缘滤波,输出像素值由邻域像素的加权组合得到,公式如下:

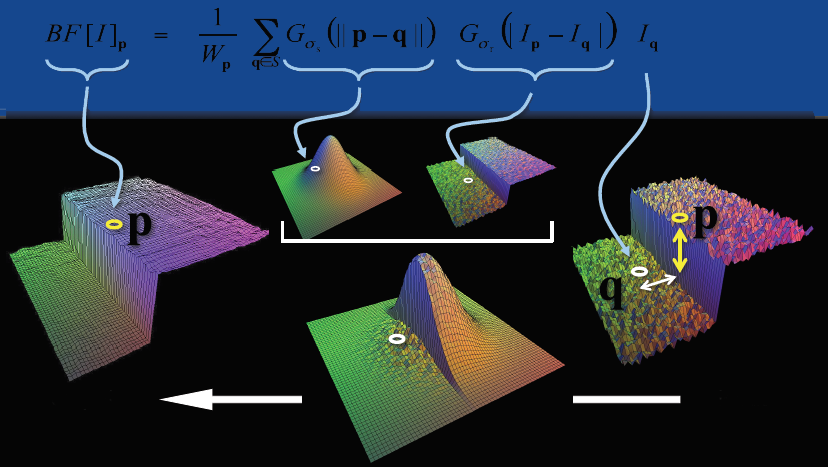
当前像素点p的值,由邻域N(p)中的所有像素点$q\in N(p)$加权求和得到,权重系数为$W_{pq}$,

$W_{pq}=G_{\sigma_s}(||p-q||)G_{\sigma_r}(||I_p-I_q||$

$G_{\sigma}$为高斯函数,均值为0,标准差为$\sigma$.$G_{\sigma_s}$,$G_{\sigma_r}$分别为定义域核,值域核,:

$G_{\sigma_s}(||p-q||)=exp(-\frac{(p_x-q_x)^2+(p_y-q_y)^2}{2\sigma_s^2})$

$p_x,p_y,q_x,q_y$表示像素点p,q在图像中的位置坐标点,$G_{\sigma_s}$表示当前的滤波输出值与像素点的位置距离有关,离p点越近的点,对p的滤波输出影响越大.

$G_{\sigma_r}(||p-q||)=exp(-\frac{(I_p-I_q)^2}{2\sigma_r^2})$

$I_p,I_q$表示像素点p,q的亮度值,表示亮度值越大的像素点对p的滤波输出影响越大.

之所有能够起到保边缘的效果,是因为在权重中引入了值域核$G_{\sigma_r}$.在边缘处,相似点p,q的亮度值相差较大,因此此时的$G_{\sigma_r}$在边缘处的跳变也很大,所以输出值在边缘处也有明显的跳变,为了更好说明,引用http://blog.csdn.net/jfuck/article/details/8932978的示意图如下:

由图像可知,原始图像在边缘处,亮度值存在明显的跳变,从而使得值域核$G_{\sigma_r}$也在边缘处存在明显跳变,从而使得滤波输出能够保留边缘信息.

Bilateral Grid

bilateral grid算法matlab代码如下:

function output = bilateralFilter( data, edge, sigmaSpatial, sigmaRange, ...
    samplingSpatial, samplingRange )

if ~exist( 'edge', 'var' ),
    edge = data;
end

inputHeight = size( data, 1 );
inputWidth = size( data, 2 );

if ~exist( 'sigmaSpatial', 'var' ),
    sigmaSpatial = min( inputWidth, inputHeight ) / 16;
end

edgeMin = min( edge( : ) );
edgeMax = max( edge( : ) );
edgeDelta = edgeMax - edgeMin;

if ~exist( 'sigmaRange', 'var' ),
    sigmaRange = 0.1 * edgeDelta;
end

if ~exist( 'samplingSpatial', 'var' ),
    samplingSpatial = sigmaSpatial;
end

if ~exist( 'samplingRange', 'var' ),
    samplingRange = sigmaRange;
end

if size( data ) ~= size( edge ),
    error( 'data and edge must be of the same size' );
end

% parameters
derivedSigmaSpatial = sigmaSpatial / samplingSpatial;
derivedSigmaRange = sigmaRange / samplingRange;

paddingXY = floor( 2 * derivedSigmaSpatial ) + 1;
paddingZ = floor( 2 * derivedSigmaRange ) + 1;

% allocate 3D grid
downsampledWidth = floor( ( inputWidth - 1 ) / samplingSpatial ) + 1 + 2 * paddingXY;
downsampledHeight = floor( ( inputHeight - 1 ) / samplingSpatial ) + 1 + 2 * paddingXY;
downsampledDepth = floor( edgeDelta / samplingRange ) + 1 + 2 * paddingZ;

gridData = zeros( downsampledHeight, downsampledWidth, downsampledDepth );
gridWeights = zeros( downsampledHeight, downsampledWidth, downsampledDepth );

% compute downsampled indices
[ jj, ii ] = meshgrid( 0 : inputWidth - 1, 0 : inputHeight - 1 );

% ii =
% 0 0 0 0 0
% 1 1 1 1 1
% 2 2 2 2 2

% jj =
% 0 1 2 3 4
% 0 1 2 3 4
% 0 1 2 3 4

% so when iterating over ii( k ), jj( k )
% get: ( 0, 0 ), ( 1, 0 ), ( 2, 0 ), ... (down columns first)

di = round( ii / samplingSpatial ) + paddingXY + 1;
dj = round( jj / samplingSpatial ) + paddingXY + 1;
dz = round( ( edge - edgeMin ) / samplingRange ) + paddingZ + 1;

% perform scatter (there's probably a faster way than this)
% normally would do downsampledWeights( di, dj, dk ) = 1, but we have to
% perform a summation to do box downsampling
for k = 1 : numel( dz ),

    dataZ = data( k ); % traverses the image column wise, same as di( k )
    if ~isnan( dataZ  ),

        dik = di( k );
        djk = dj( k );
        dzk = dz( k );

        gridData( dik, djk, dzk ) = gridData( dik, djk, dzk ) + dataZ;
        gridWeights( dik, djk, dzk ) = gridWeights( dik, djk, dzk ) + 1;

    end
end

% make gaussian kernel
kernelWidth = 2 * derivedSigmaSpatial + 1;
kernelHeight = kernelWidth;
kernelDepth = 2 * derivedSigmaRange + 1;

halfKernelWidth = floor( kernelWidth / 2 );
halfKernelHeight = floor( kernelHeight / 2 );
halfKernelDepth = floor( kernelDepth / 2 );

[gridX, gridY, gridZ] = meshgrid( 0 : kernelWidth - 1, 0 : kernelHeight - 1, 0 : kernelDepth - 1 );
gridX = gridX - halfKernelWidth;
gridY = gridY - halfKernelHeight;
gridZ = gridZ - halfKernelDepth;
gridRSquared = ( gridX .* gridX + gridY .* gridY ) / ( derivedSigmaSpatial * derivedSigmaSpatial ) + ( gridZ .* gridZ ) / ( derivedSigmaRange * derivedSigmaRange );
kernel = exp( -0.5 * gridRSquared );

% convolve
blurredGridData = convn( gridData, kernel, 'same' );
blurredGridWeights = convn( gridWeights, kernel, 'same' );

% divide
blurredGridWeights( blurredGridWeights == 0 ) = -2; % avoid divide by 0, won't read there anyway
normalizedBlurredGrid = blurredGridData ./ blurredGridWeights;
normalizedBlurredGrid( blurredGridWeights < -1 ) = 0; % put 0s where it's undefined
blurredGridWeights( blurredGridWeights < -1 ) = 0; % put zeros back

% upsample
[ jj, ii ] = meshgrid( 0 : inputWidth - 1, 0 : inputHeight - 1 ); % meshgrid does x, then y, so output arguments need to be reversed
% no rounding
di = ( ii / samplingSpatial ) + paddingXY + 1;
dj = ( jj / samplingSpatial ) + paddingXY + 1;
dz = ( edge - edgeMin ) / samplingRange + paddingZ + 1;

% interpn takes rows, then cols, etc
% i.e. size(v,1), then size(v,2), ...
output = interpn( normalizedBlurredGrid, di, dj, dz );