主要分析从局部坐标系变换到全局坐标系下的坐标转换公式。首先对全局坐标系进行描述,如图1,o-xyz即全局坐标系,O-X'Y'Z'即在o-xyz坐标系中定义的局部坐标系,两个坐标系之间的关系如下:这个O-X'Y'Z'的Z'轴会经过o-xyz坐标系的坐标原点,Y'轴会经过o-xyz坐标系的z轴,X'轴与Y'轴和Z'轴垂直构成右手坐标系。
设O'点在xoy平面的投影为O'',连接oO'',由于O'X'与oO'O''平面垂直,所以O'X'与oO''垂直,并且oO'O''平面与oxy平面垂直,所以o'X'与oxy平面平行。并且O'X'与ox轴的夹角与oO''与o-xyz坐标系y轴负半轴的夹角是相等的,设这个角为α(根据等角的补角相等很容易证明)。现在我们需要根据模型在O-X'Y'Z'中的坐标求解其在o-xyz系的坐标,必须求解从o-xyz到O-X'Y'Z'的变换矩阵。已知O'点在o-xyz坐标系下的坐标为(xo,y0,z0) 。
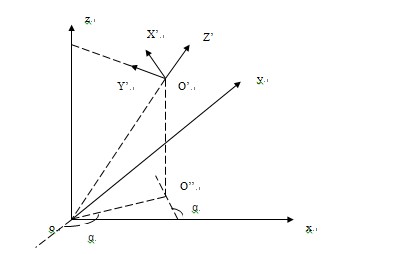
图1
求解从o-xyz到O-X'Y'Z'的变换矩阵,需要首先执行旋转操作,然后执行平移操作,执行完旋转操作后的坐标系关系应该如图2所示,O1-X1Y1Z1的三个坐标轴与图1中的O-X'Y'Z'的三个坐标轴都平行,并且O1-X1Y1Z1的坐标原点与o-xyz的坐标原点重合,当再次执行平移操作时O1-X1Y1Z1就会与O-X'Y'Z'坐标系重合。
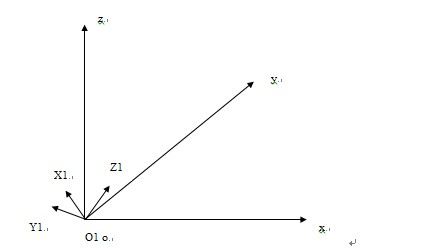
图2
现在分析如何对o-xyz执行旋转操作是之能变换到O1-X1Y1Z1的位置,前面已经知道o'x'与xoy平面是平行的,那么此时O1X1与xoy平面也平行,并且由于O1X1经过xoy平面的原点o,所以O1X1在xoy这个平面内。并且上面已经证明O'X'与o轴的夹角与oO''与o-xyz坐标系y轴负半轴的夹角是相等的,由于已知O'点的坐标,所以我们可以求得O''与o-xyz坐标系y轴负半轴的夹角α,这个角等于图1-2中O1X1与ox轴之间的夹角。这样先将o-xyz坐标系绕z轴逆时针旋转角α,此时ox轴会旋转到O1X1处,再绕O1X1逆时针旋转oz与O1Z1之间的夹角(设为β)即将o-xyz旋转到了O1-X1Y1Z1的位置。
分析完全局坐标系与局部坐标系之间的位置关系和需要进行怎样的旋转和平移操作以后下面分析这些旋转和平移操作的变换公式。
根据上面的分析我们知道要从o-xyz变换到O-X'Y'Z',需要首先绕z轴逆时针旋转α,然后再绕x轴旋转后的轴逆时针旋转β(α,β的解释参数上面的定义),此时o-xyz会变换成O1-X1Y1Z1,然后根据O1的坐标(xo,y0,z0)进行平移即完成了从o-xyz到O-X'Y'Z'的变换。 然后根据上面介绍的在三维坐标系下的平移和旋转矩阵得到最终的变换矩阵M可以表示为:
附上一份在网上找到的讲解坐标变换的ppt,主要是变换矩阵的实现。























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








