一、先来个平面旋转的分析:
两角和(差)公式

推导
旋转变换一般是按照某个圆心点,以一定半径 r 旋转一定的角度α,为了简单起见我们给出下面的情景
假定点A(x,y)想经过旋转变换到达B(x',y'),已知旋转角度α和点A坐标,计算出点B
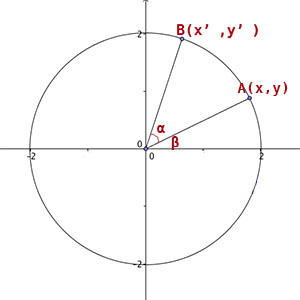
要计算点B则分别计算他的x'和y'分量

根据矩阵乘法计算规则,可以推出

只要给出旋转角度,计算出矩阵,然后使用这个矩阵分别左乘每一个点,就能计算出这个点旋转后的点坐标 这样我们就可以通过矩阵变换坐标了
二、延伸到三维坐标:
坐标的旋转变换在很多地方都会用到,比如机器视觉中的摄像机标定、图像处理中的图像旋转、游戏编程等。
任何维的旋转可以表述为向量与合适尺寸的方阵的乘积。最终一个旋转等价于在另一个不同坐标系下对点位置的重新表述。坐标系旋转角度θ则等同于将目标点围绕坐标原点反方向旋转同样的角度θ。
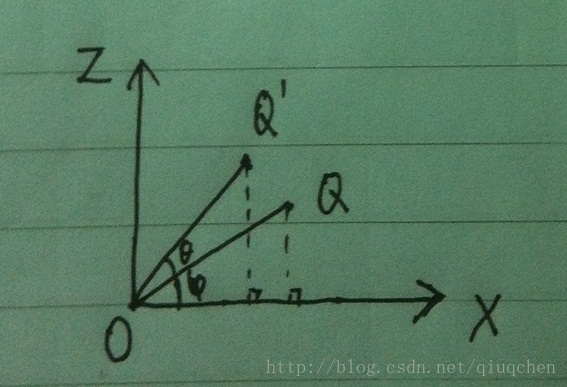
若以坐标系的三个坐标轴X、Y、Z分别作为旋转轴,则点实际上只在垂直坐标轴的平面上作二维旋转。
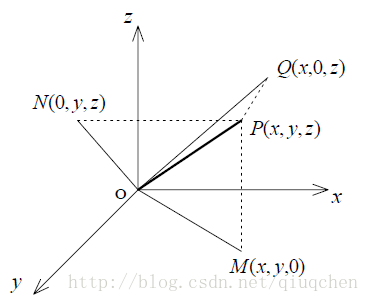
图1 直角坐标系XYZ
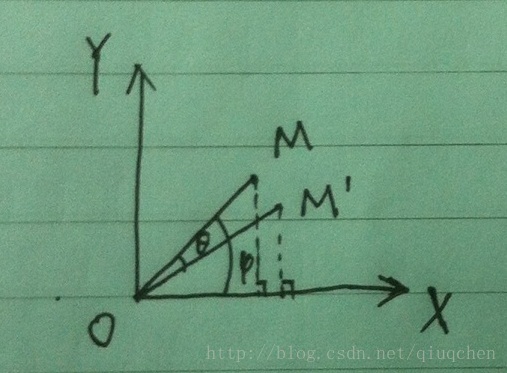
图2 向量绕Z轴旋转示意图

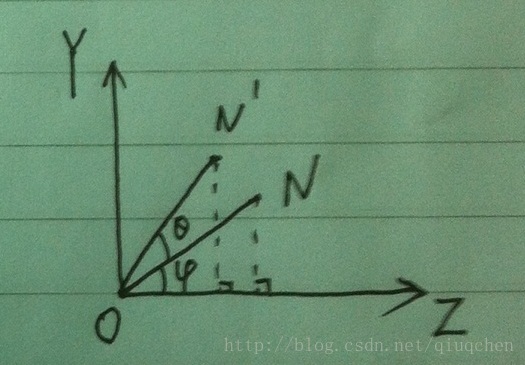
图3 向量绕X轴旋转示意图

































 2588
2588

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








