day01无人机理论

坐标系及欧拉角 

目录(?)[-]

1. 坐标系
   1. 1右手定则
   2. 2惯性坐标系与机体坐标系定义
2. 姿态表示-欧拉角
   1. 1欧拉角的定义
   2. 2 欧拉角变化率与机体角速度的关系

根据学习北航《多旋翼飞行器设计与控制》的课件，结合自己理解、推导写的笔记，以此加深理解，与大家交流。

1.坐标系

1.1右手定则

采用的坐标系和定义的角度正方向沿用右手定则。

1.2惯性坐标系与机体坐标系定义

地球表面惯性坐标系（下标e）用于研究多旋翼飞行器相对于地面的运动状态，确定机体的空间位置坐标。它忽略地球曲率，即将地球表面假设成一张平面。在地面上选一点作为多旋翼飞行器起飞位置。

机体坐标系（下标b），其原点 取在多旋翼的重心上，坐标系与多旋翼固连。
轴在多旋翼对称平面内指向机头。

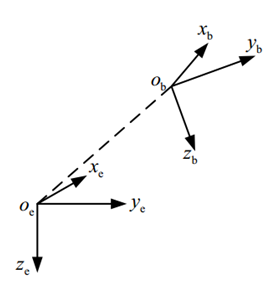
定义三个单位向量

e1=⎡⎣⎢100⎤⎦⎥, e2=⎡⎣⎢010⎤⎦⎥, e3=⎡⎣⎢001⎤⎦⎥

在惯性坐标系中，沿着 xe,ye,ze 坐标轴的单位向量可表示为

{e1,e2,e3}

在机体坐标系下，沿 xb,yb,zb 的坐标轴的单位向量满足（注：左上标b表示向量在机体坐标系的表示）

b b1=e1,b b2=e2,b b3=e3

在地球惯性坐标系中，沿 xb,yb,zb 的坐标轴的单位向量可表示为（注：左上标e表示向量在惯性坐标系的表示）

{e b1,e b2,e b3}

2.姿态表示-欧拉角

2.1欧拉角的定义

机体坐标系与地面惯性坐标系之间的夹角就是飞机的姿态角，又称欧拉角。
（1）俯仰角 θ ： 机体轴与地平面（水平面）之间的夹角，飞机抬头为正。
（2）偏航角（方位角） ψ ：机体轴在水平面上的投影与地轴之间的夹角，以机头右偏为正。
（3）滚转角（倾斜角） ϕ ：飞机对称面绕机体轴 转过的角度，右滚为正。

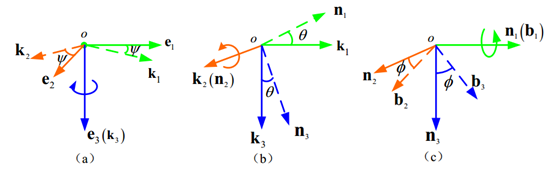
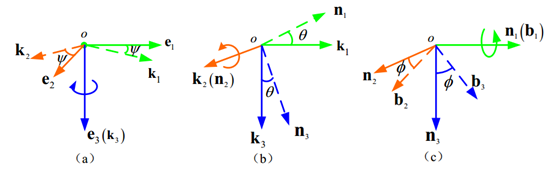
可以通过绕 e3,k2,n1 轴分别旋转欧拉角 ψ,θ,ϕ 将地球表面惯性坐标系转动到机体坐标系。

2.2 欧拉角变化率与机体角速度的关系

若机体旋转的角速度为

b ω=[ωxb,ωyb,ωzb]T

那么有（注：上标b表示向量在机体坐标系下的坐标表示，这里的机体坐标系当然指的是经过三次旋转后的机体坐标系，如图所示）。

b ω= ψ∙˙b k3+θ∙˙b n2+ϕ∙˙b b1

在最新的机体坐标系下，显然有

n1=b1=[1,0,0]T

如图（c）， n2 可以由 b2 绕 n1 轴转过 −ϕ 而得到，因此

n2=⎡⎣⎢1000cosϕsin(−ϕ)−sin(−ϕ)0cosϕ⎤⎦⎥⎡⎣⎢010⎤⎦⎥=⎡⎣⎢0cosϕ−sinϕ⎤⎦⎥

如图（c），（b），（d）所示， k3 可以由 b3 经过旋转 −ϕ,−θ 角度得到，因此

k3=⎡⎣⎢cosϕ0−sin(−θ)010sin(−θ)0cosϕ⎤⎦⎥⎡⎣⎢cosϕ0sin(−ϕ)010−sin(−ϕ)0cosϕ⎤⎦⎥⎡⎣⎢001⎤⎦⎥=⎡⎣⎢−sinθsinϕcosθcosϕcosθ⎤⎦⎥

因此

b ω= ψ∙˙⎡⎣⎢−sinθsinϕcosθcosϕcosθ⎤⎦⎥+θ∙˙⎡⎣⎢0cosϕ−sinϕ⎤⎦⎥+ϕ˙∙⎡⎣⎢100⎤⎦⎥=⎡⎣⎢1000cosϕ−sinϕ−sinθsinϕcosθcosϕcosθ⎤⎦⎥⎡⎣⎢⎢ϕθ˙ψ˙˙⎤⎦⎥⎥

因此有

⎡⎣⎢b ωxb ωyb ωz⎤⎦⎥=⎡⎣⎢1000cosϕ−sinϕ−sinθsinϕcosθcosϕcosθ⎤⎦⎥⎡⎣⎢⎢ϕθ˙ψ˙˙⎤⎦⎥⎥

进一步有

Θ˙=Wb ω

其中

Θ=⎡⎣⎢ϕθψ⎤⎦⎥,

W=⎡⎣⎢1000cosϕ−sinϕ−sinθsinϕcosθcosϕcosθ⎤⎦⎥−1=⎡⎣⎢100tanθsinϕcosϕ−sinϕ/cosθtanθcosϕ−sinϕcosϕ/cosθ⎤⎦⎥

当 θ=±π2 时，出现奇异问题。

当 ϕ,θ≈0 时，可以认为

⎡⎣⎢⎢ϕθ˙ψ˙˙⎤⎦⎥⎥=⎡⎣⎢b ωxb ωyb ωz⎤⎦⎥